Woche 4

Überblick

Thema	Inhalte	Folien	Video	Buch	Training
3	Stammfunktionen	1-6	3a	4.1	4.1
	Einfach Integrationsregeln	7-13	3b	4.2	4.2.1
	Anwendungen	14-22	3c-e	4.3	4.3
					Quiz
					PS-Übungsaufgabe

Stammfunktionen

Einfach Integrationsregeln

Anwendungen

Quiz

Es sei \(F(x)\) eine differenzierbare Funktion und es sei \(F'(x) = f(x)\). Welche Aussagen sind dann richtig?

Für die Berechnung des bestimmten Integrals muss die Stammfunktion \(F(x) + c\) mit \(c = 0\) verwendet werden.\(F(x)\) ist eine Stammfunktion von \(f'(x)\).\(F(x) + c\) ist eine Stammfunktion von \(f(x)\).\(f(x) + c\) ist eine Ableitung von \(F(x)\).\(\int_a^b f(x) \text{d} x = F(b - a)\).

Details zur Integralrechnung werden auf den VO-Folien im Abschnitt Stammfunktionen vorgestellt sowie im Buch im Abschnitt 4.

Falsch. Bei der Berechnung des bestimmten Integrals spielt die Wahl der Konstante \(c\) keine Rolle.
Falsch. \(f(x)\) ist eine Stammfunktion von \(f'(x)\).
Richtig. Die Stammfunktion ist nur bis auf eine additive Konstante \(c\) bestimmt.
Falsch. \(f(x) + c\) wäre eine Ableitung von \(F(x) + c \cdot x\).
Falsch. \(\int_a^b f(x) \text{d} x = F(b) - F(a)\).

Aus einem Stück Metall soll eine Form geschnitten werden, die durch die Funktion

\(f(x) = -x^2 + 16.4x\)

zwischen den Punkten \(x_{min} = 2\) und \(x_{max} = 12\) begrenzt wird (\(x\) und \(f(x)\) in \(\text{dm}\)). \(122\) solcher Teile sollen zu einem Preis von \(2.8~\text{GE}/\text{dm}^2\) von beiden Seiten mit einem Speziallack überzogen werden. Abschließend werden die Metallstücke entlang des Punktes \(x=6\) in zwei Teilstücke geschnitten.

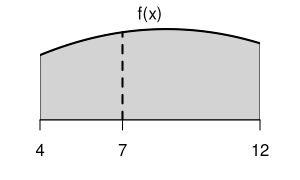
Berechnen Sie die Fläche einer Seite eines gesamten Metallstücks.

Berechnen Sie die Fläche einer Seite des kleineren Teilstücks nach dem Teilungsprozess an der Stelle \(x=6\).

Berechnen Sie die Kosten der beidseitigen Lackierung aller \(122\) gesamten Metallstücke.

Die Geschwindigkeit eines Sportautos in \(km/h\) bei der Beschleunigung verläuft nach folgender Gleichung: \[\begin{aligned} f(x) = 0.2\cdot x^3 - 0.6 \cdot x^2 + 3.5 \cdot x + 37 \end{aligned}\] Wobei \(x\) die Zeit in Sekunden seit Beginn der Messung ist (\(x = 0\)).

Wie hoch ist die mittlere Geschwindigkeit zwischen \(0\) und \(11\) Sekunden?

PS-Übungsaufgabe

Sie werden von der Stock AG beauftragt, für das laufende Jahr eine Analyse des Lagerbestandes durchzuführen. Sie wissen, dass zu Beginn des Jahres (also in Woche \(w = 0\)) \(9812\) Mengeneinheiten auf Lager waren und dass der Lagerbestand in der Vergangenheit mit einer relativen (prozentuellen) wöchentlichen Änderung von \(13.40\)% abgenommen hat. Gehen Sie davon aus, dass diese auch weiterhin gültig ist, und beantworten Sie folgende Fragen.

Wie hoch ist der Lagerbestand nach \(22\) Wochen?

Mit welcher nominellen Wachstumsrate (pro Woche, in Prozent, positiv) nimmt der Lagerbestand ab?

Wie groß ist der durchschnittliche Lagerbestand in den ersten \(22\) Wochen?

Mit welcher momentanen Änderungsrate (positiv) sinkt der Lagerbestand pro Woche zum Zeitpunkt \(w = 22\)?

Wie viele Mengeneinheiten verlassen durchschnittlich das Lager pro Woche (positiv) im Zeitraum von \(w = 22\) bis \(w = 30\) Wochen?