5 Wahrscheinlichkeitsrechnung

Grundbegriffe

a

Ein \(6\)-seitiger, fairer Würfel mit den Augenzahlen \(1, 2, 3, 4, 5, 6\) wird zweimal geworfen.

Wie groß ist die Wahrscheinlichkeit einer Augensumme von \(8\)? (Geben Sie das Ergebnis in Prozent an.)

Es handelt sich hier um Laplace-Wahrscheinlichkeiten, d.h., alle Augenzahlen haben die gleiche Wahrscheinlichkeit. Die gesuchte Wahrscheinlichkeit errechnet sich daher als Quotient günstige Fälle dividiert durch mögliche Fälle.

Wir können die Augensumme beim zweimaligen Würfeln in Matrixform abbilden.

	1	2	3	4	5	6
1	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)
2	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)
3	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)
4	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)
5	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)	\(11\)
6	\(7\)	\(8\)	\(9\)	\(10\)	\(11\)	\(12\)

Es kommen also \(5\) günstige auf \(36\) mögliche Fälle. Die gesuchte Wahrscheinlichkeit beträgt daher \[\begin{aligned} P(\mbox{Augensumme ist 8}) = \frac{5}{36} = 0.138889. \end{aligned}\] Die Wahrscheinlichkeit beträgt also \(13.89\%\).

Ein \(6\)-seitiger, fairer Würfel mit den Augenzahlen \(1, 2, 3, 4, 5, 6\) wird zweimal geworfen.

Wie groß ist die Wahrscheinlichkeit einer Augensumme von \(7\)? (Geben Sie das Ergebnis in Prozent an.)

Es handelt sich hier um Laplace-Wahrscheinlichkeiten, d.h., alle Augenzahlen haben die gleiche Wahrscheinlichkeit. Die gesuchte Wahrscheinlichkeit errechnet sich daher als Quotient günstige Fälle dividiert durch mögliche Fälle.

Wir können die Augensumme beim zweimaligen Würfeln in Matrixform abbilden.

	1	2	3	4	5	6
1	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)
2	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)
3	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)
4	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)
5	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)	\(11\)
6	\(7\)	\(8\)	\(9\)	\(10\)	\(11\)	\(12\)

Es kommen also \(6\) günstige auf \(36\) mögliche Fälle. Die gesuchte Wahrscheinlichkeit beträgt daher \[\begin{aligned} P(\mbox{Augensumme ist 7}) = \frac{6}{36} = 0.166667. \end{aligned}\] Die Wahrscheinlichkeit beträgt also \(16.67\%\).

Ein \(6\)-seitiger, fairer Würfel mit den Augenzahlen \(1, 2, 3, 4, 5, 6\) wird zweimal geworfen.

Wie groß ist die Wahrscheinlichkeit einer Augensumme von \(7\)? (Geben Sie das Ergebnis in Prozent an.)

Es handelt sich hier um Laplace-Wahrscheinlichkeiten, d.h., alle Augenzahlen haben die gleiche Wahrscheinlichkeit. Die gesuchte Wahrscheinlichkeit errechnet sich daher als Quotient günstige Fälle dividiert durch mögliche Fälle.

Wir können die Augensumme beim zweimaligen Würfeln in Matrixform abbilden.

	1	2	3	4	5	6
1	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)
2	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)
3	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)
4	\(5\)	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)
5	\(6\)	\(7\)	\(8\)	\(9\)	\(10\)	\(11\)
6	\(7\)	\(8\)	\(9\)	\(10\)	\(11\)	\(12\)

Es kommen also \(6\) günstige auf \(36\) mögliche Fälle. Die gesuchte Wahrscheinlichkeit beträgt daher \[\begin{aligned} P(\mbox{Augensumme ist 7}) = \frac{6}{36} = 0.166667. \end{aligned}\] Die Wahrscheinlichkeit beträgt also \(16.67\%\).

b

Man betrachte zwei vierseitige Würfel. Der erste Würfel A hat die Ziffern \(1, 7, 10, 10\) aufgedruckt, der zweite Würfel B hat die Ziffern \(1, 4, 5, 7\) aufgedruckt.

Mit welcher Wahrscheinlichkeit gewinnt A, wenn beide Würfel einmal geworfen werden und die höhere Augenzahl gewinnt? (Geben Sie das Ergebnis in Prozent an.)

Am einfachsten wird das Würfeln der beiden Würfel in Matrixform dargestellt. Die Matrix zeigt, ob A mit dieser Augenkombination gewinnt:

	1	4	5	7
1	nein	nein	nein	nein
7	ja	ja	ja	nein
10	ja	ja	ja	ja
10	ja	ja	ja	ja

Es kommen also \(11\) günstige auf \(16\) mögliche Fälle. Die Wahrscheinlichkeit, dass A gewinnt beträgt also \[\begin{aligned} P(\mbox{W\"urfel A gewinnt}) = \frac{11}{16} = 0.6875. \end{aligned}\] Die Wahrscheinlichkeit beträgt also \(68.75\%\).

Man betrachte zwei vierseitige Würfel. Der erste Würfel A hat die Ziffern \(1, 5, 7, 9\) aufgedruckt, der zweite Würfel B hat die Ziffern \(3, 3, 6, 8\) aufgedruckt.

Mit welcher Wahrscheinlichkeit gewinnt A, wenn beide Würfel einmal geworfen werden und die höhere Augenzahl gewinnt? (Geben Sie das Ergebnis in Prozent an.)

Am einfachsten wird das Würfeln der beiden Würfel in Matrixform dargestellt. Die Matrix zeigt, ob A mit dieser Augenkombination gewinnt:

	3	3	6	8
1	nein	nein	nein	nein
5	ja	ja	nein	nein
7	ja	ja	ja	nein
9	ja	ja	ja	ja

Es kommen also \(9\) günstige auf \(16\) mögliche Fälle. Die Wahrscheinlichkeit, dass A gewinnt beträgt also \[\begin{aligned} P(\mbox{W\"urfel A gewinnt}) = \frac{9}{16} = 0.5625. \end{aligned}\] Die Wahrscheinlichkeit beträgt also \(56.25\%\).

Man betrachte zwei vierseitige Würfel. Der erste Würfel A hat die Ziffern \(2, 3, 4, 5\) aufgedruckt, der zweite Würfel B hat die Ziffern \(1, 2, 3, 10\) aufgedruckt.

Mit welcher Wahrscheinlichkeit gewinnt A, wenn beide Würfel einmal geworfen werden und die höhere Augenzahl gewinnt? (Geben Sie das Ergebnis in Prozent an.)

Am einfachsten wird das Würfeln der beiden Würfel in Matrixform dargestellt. Die Matrix zeigt, ob A mit dieser Augenkombination gewinnt:

	1	2	3	10
2	ja	nein	nein	nein
3	ja	ja	nein	nein
4	ja	ja	ja	nein
5	ja	ja	ja	nein

Es kommen also \(9\) günstige auf \(16\) mögliche Fälle. Die Wahrscheinlichkeit, dass A gewinnt beträgt also \[\begin{aligned} P(\mbox{W\"urfel A gewinnt}) = \frac{9}{16} = 0.5625. \end{aligned}\] Die Wahrscheinlichkeit beträgt also \(56.25\%\).

c

Ein fairer, \(5\)-seitiger Würfel mit den Augenzahlen \(1, 2, 4, 8, 9\) wird zweimal geworfen.

Wie groß ist die Wahrscheinlichkeit, dass die Augensumme größer als \(8\) ist? (Geben Sie das Ergebnis in Prozent an.)

Es handelt sich hier um Laplace-Wahrscheinlichkeiten, d.h., alle Augenzahlen haben die gleiche Wahrscheinlichkeit. Die gesuchte Wahrscheinlichkeit errechnet sich daher als Quotient der Anzahl günstiger zu möglicher Fälle. Die Tabelle der möglichen Augensummen ist:

	1	2	4	8	9
1	\(2\)	\(3\)	\(5\)	\(9\)	\(10\)
2	\(3\)	\(4\)	\(6\)	\(10\)	\(11\)
4	\(5\)	\(6\)	\(8\)	\(12\)	\(13\)
8	\(9\)	\(10\)	\(12\)	\(16\)	\(17\)
9	\(10\)	\(11\)	\(13\)	\(17\)	\(18\)

Es kommen also \(16\) günstige auf \(25\) mögliche Fälle. Die gesuchte Wahrscheinlichkeit beträgt daher:

\[\begin{aligned} P(\textrm{Augensumme} > 8) = \frac{16}{25} = 0.64. \end{aligned}\]

Die Wahrscheinlichkeit beträgt also \(64.00\%\).

Ein fairer, \(5\)-seitiger Würfel mit den Augenzahlen \(2, 3, 6, 7, 9\) wird zweimal geworfen.

Wie groß ist die Wahrscheinlichkeit, dass die Augensumme größer als \(7\) ist? (Geben Sie das Ergebnis in Prozent an.)

Es handelt sich hier um Laplace-Wahrscheinlichkeiten, d.h., alle Augenzahlen haben die gleiche Wahrscheinlichkeit. Die gesuchte Wahrscheinlichkeit errechnet sich daher als Quotient der Anzahl günstiger zu möglicher Fälle. Die Tabelle der möglichen Augensummen ist:

	2	3	6	7	9
2	\(4\)	\(5\)	\(8\)	\(9\)	\(11\)
3	\(5\)	\(6\)	\(9\)	\(10\)	\(12\)
6	\(8\)	\(9\)	\(12\)	\(13\)	\(15\)
7	\(9\)	\(10\)	\(13\)	\(14\)	\(16\)
9	\(11\)	\(12\)	\(15\)	\(16\)	\(18\)

Es kommen also \(21\) günstige auf \(25\) mögliche Fälle. Die gesuchte Wahrscheinlichkeit beträgt daher:

\[\begin{aligned} P(\textrm{Augensumme} > 7) = \frac{21}{25} = 0.84. \end{aligned}\]

Die Wahrscheinlichkeit beträgt also \(84.00\%\).

Ein fairer, \(4\)-seitiger Würfel mit den Augenzahlen \(6, 8, 8, 9\) wird zweimal geworfen.

Wie groß ist die Wahrscheinlichkeit, dass die Augensumme größer als \(16\) ist? (Geben Sie das Ergebnis in Prozent an.)

Es handelt sich hier um Laplace-Wahrscheinlichkeiten, d.h., alle Augenzahlen haben die gleiche Wahrscheinlichkeit. Die gesuchte Wahrscheinlichkeit errechnet sich daher als Quotient der Anzahl günstiger zu möglicher Fälle. Die Tabelle der möglichen Augensummen ist:

	6	8	8	9
6	\(12\)	\(14\)	\(14\)	\(15\)
8	\(14\)	\(16\)	\(16\)	\(17\)
8	\(14\)	\(16\)	\(16\)	\(17\)
9	\(15\)	\(17\)	\(17\)	\(18\)

Es kommen also \(5\) günstige auf \(16\) mögliche Fälle. Die gesuchte Wahrscheinlichkeit beträgt daher:

\[\begin{aligned} P(\textrm{Augensumme} > 16) = \frac{5}{16} = 0.3125. \end{aligned}\]

Die Wahrscheinlichkeit beträgt also \(31.25\%\).

d

Eine stetige Zufallsvariable \(X\) hat folgende Dichtefunktion

\[f(x)= \left\{ \begin{array}{cc} \frac{1}{x\ln(20)} & 1 \leq x \leq 20 \\ 0 & \mbox{sonst} \end{array} \right.\]

Berechnen Sie \(P(2.3 < X < 17.1)\). (Geben Sie das Ergebnis in Prozent an.)

Die Verteilungsfunktion im Bereich \(1 \leq x \leq 20\) ist gegeben durch: \[\begin{aligned} F(x) & = & \int_{-\infty}^{x} f(t) \ \text{d} t \\ & = & \int_{1}^{x} \frac{1}{t \ln(20)} \ \text{d} t \\ & = & \frac{1}{\ln(20)} \int_{1}^{x} \frac{1}{t} \ \text{d} t \\ & = & \frac{1}{\ln(20)} \left[ \ln(t) \right]_{1}^{x} \\ & = & \frac{1}{\ln(20)} \left( \ln(x) - \ln(1) \right) \\ & = & \frac{\ln(x)}{\ln(20)}. \end{aligned}\]

Damit ergibt sich: \(P(2.3 < X < 17.1) = F(17.1) - F(2.3) = 0.669676\). Dies entspricht \(66.97\%\).

Eine stetige Zufallsvariable \(X\) hat folgende Dichtefunktion

\[f(x)= \left\{ \begin{array}{cc} \frac{1}{x\ln(6)} & 1 \leq x \leq 6 \\ 0 & \mbox{sonst} \end{array} \right.\]

Berechnen Sie \(P(2.4 \leq X \leq 4.8)\). (Geben Sie das Ergebnis in Prozent an.)

Die Verteilungsfunktion im Bereich \(1 \leq x \leq 6\) ist gegeben durch: \[\begin{aligned} F(x) & = & \int_{-\infty}^{x} f(t) \ \text{d} t \\ & = & \int_{1}^{x} \frac{1}{t \ln(6)} \ \text{d} t \\ & = & \frac{1}{\ln(6)} \int_{1}^{x} \frac{1}{t} \ \text{d} t \\ & = & \frac{1}{\ln(6)} \left[ \ln(t) \right]_{1}^{x} \\ & = & \frac{1}{\ln(6)} \left( \ln(x) - \ln(1) \right) \\ & = & \frac{\ln(x)}{\ln(6)}. \end{aligned}\]

Damit ergibt sich: \(P(2.4 \leq X \leq 4.8) = F(4.8) - F(2.4) = 0.386853\). Dies entspricht \(38.69\%\).

Eine stetige Zufallsvariable \(X\) hat folgende Dichtefunktion

\[f(x)= \left\{ \begin{array}{cc} \frac{1}{x\ln(15)} & 1 \leq x \leq 15 \\ 0 & \mbox{sonst} \end{array} \right.\]

Berechnen Sie \(P(4.3 < X \leq 6)\). (Geben Sie das Ergebnis in Prozent an.)

Die Verteilungsfunktion im Bereich \(1 \leq x \leq 15\) ist gegeben durch: \[\begin{aligned} F(x) & = & \int_{-\infty}^{x} f(t) \ \text{d} t \\ & = & \int_{1}^{x} \frac{1}{t \ln(15)} \ \text{d} t \\ & = & \frac{1}{\ln(15)} \int_{1}^{x} \frac{1}{t} \ \text{d} t \\ & = & \frac{1}{\ln(15)} \left[ \ln(t) \right]_{1}^{x} \\ & = & \frac{1}{\ln(15)} \left( \ln(x) - \ln(1) \right) \\ & = & \frac{\ln(x)}{\ln(15)}. \end{aligned}\]

Damit ergibt sich: \(P(4.3 < X \leq 6) = F(6) - F(4.3) = 0.12302\). Dies entspricht \(12.30\%\).

e

Jonas möchte ein Duschbad nehmen. Die Wartezeit \(W\) (in Stunden) auf den nächsten Anruf seiner Freundin ist exponentialverteilt mit der Wahrscheinlichkeit \[P(W \le t) = \left\{ \begin{array}{ll} 0 & t < 0 \\ 1 - \exp(-2t) & t \geq 0 \\ \end{array} \right.\]

Wie groß ist die Wahrscheinlichkeit, dass Jonas nicht gestört wird, wenn er \(17\) Minuten duscht? (Geben Sie das Ergebnis in Prozent an.)

Eine Duschzeit von \(17\) Minuten entspricht \[\begin{aligned} \frac{17}{60} = 0.283333~\text{Stunden}. \end{aligned}\]

Gesucht ist somit die Warscheinlichkeit \(1 - P(W \le 0.283333)\).

Diese errechnet sich durch \[\begin{aligned} 1 - P(W \le 0.283333) &=& 1 - (1 - \exp(-2 \cdot 0.283333))\\&=& \exp(-2 \cdot 0.283333)\\&=& 0.567414 \end{aligned}\] Die Wahrscheinlichkeit, dass Jonas bei einem \(17\)-minütigen Duschbad von seiner Freundin nicht gestört wird, beträgt somit \(56.74\) %.

Lena möchte ein Duschbad nehmen. Die Wartezeit \(W\) (in Stunden) auf den nächsten Anruf ihrer Freundin ist exponentialverteilt mit der Wahrscheinlichkeit \[P(W \le t) = \left\{ \begin{array}{ll} 0 & t < 0 \\ 1 - \exp(-1.6t) & t \geq 0 \\ \end{array} \right.\]

Wie groß ist die Wahrscheinlichkeit, dass Lena gestört wird, wenn sie \(24\) Minuten duscht? (Geben Sie das Ergebnis in Prozent an.)

Eine Duschzeit von \(24\) Minuten entspricht \[\begin{aligned} \frac{24}{60} = 0.4~\text{Stunden}. \end{aligned}\]

Gesucht ist somit die Warscheinlichkeit \(P(W \le 0.4)\).

Diese errechnet sich durch \[\begin{aligned} P(W \le 0.4) &=& P(W \le 0.4)\\&=& 1 - \exp(-1.6 \cdot 0.4)\\&=& 0.472708 \end{aligned}\] Die Wahrscheinlichkeit, dass Lena bei einem \(24\)-minütigen Duschbad von ihrer Freundin gestört wird, beträgt somit \(47.27\) %.

Lara möchte ein Duschbad nehmen. Die Wartezeit \(W\) (in Stunden) auf den nächsten Anruf ihrer Freundin ist exponentialverteilt mit der Wahrscheinlichkeit \[P(W \le t) = \left\{ \begin{array}{ll} 0 & t < 0 \\ 1 - \exp(-2.1t) & t \geq 0 \\ \end{array} \right.\]

Wie groß ist die Wahrscheinlichkeit, dass Lara gestört wird, wenn sie \(29\) Minuten duscht? (Geben Sie das Ergebnis in Prozent an.)

Eine Duschzeit von \(29\) Minuten entspricht \[\begin{aligned} \frac{29}{60} = 0.483333~\text{Stunden}. \end{aligned}\]

Gesucht ist somit die Warscheinlichkeit \(P(W \le 0.483333)\).

Diese errechnet sich durch \[\begin{aligned} P(W \le 0.483333) &=& P(W \le 0.483333)\\&=& 1 - \exp(-2.1 \cdot 0.483333)\\&=& 0.637598 \end{aligned}\] Die Wahrscheinlichkeit, dass Lara bei einem \(29\)-minütigen Duschbad von ihrer Freundin gestört wird, beträgt somit \(63.76\) %.

f

Ein diskrete Zufallsvariable \(X\) hat folgende Wahrscheinlichkeitsfunktion

\[ f(x)= \left\{ \begin{array}{cc} \frac{280}{761} \cdot \frac{1}{x} & x = 1, 2, \dots, 8 \\ 0 & \mbox{sonst} \end{array} \right. \]

Berechnen Sie die Verteilungsfunktion \(F(x)\).

\(x\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)
\(F(x)\)

Berechnen Sie folgende Wahrscheinlichkeiten:

\(P(X = 4) =\)

\(P(X \geq 7) =\)

\(P(4 \leq X < 7) =\)

Die Verteilungsfunktion ergibt sich als kumulative Summe der Werte aus der Wahrscheinlichkeitsfunktion \(f(x)\), d.h. \(F(x) = f(1) + \dots + f(x)\) für \(x = 1, 2, \dots, 8\).

\(x\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)
\(F(x)\)	\(0.3679\)	\(0.5519\)	\(0.6746\)	\(0.7665\)	\(0.8401\)	\(0.9014\)	\(0.9540\)	\(1.0000\)

Damit können die drei gesuchten Wahrscheinlichkeiten berechnet werden:

\[\begin{eqnarray*} P(X = 4) & = & f(4) = \frac{280}{761} \cdot \frac{1}{4} = 0.092\\ P(X \geq 7) & = & 1 - P(X \leq 6) = 1 - F(6) = 1 - 0.9014 = 0.0986\\ P(4 \leq X < 4) & = & P(X \leq 6) - P(X \leq 3) = F(6) - F(3) \\ & = & 0.9014 - 0.6746 = 0.2269 \end{eqnarray*}\]

Ein diskrete Zufallsvariable \(X\) hat folgende Wahrscheinlichkeitsfunktion

\[ f(x)= \left\{ \begin{array}{cc} \frac{60}{137} \cdot \frac{1}{x} & x = 1, 2, \dots, 5 \\ 0 & \mbox{sonst} \end{array} \right. \]

Berechnen Sie die Verteilungsfunktion \(F(x)\).

\(x\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)
\(F(x)\)

Berechnen Sie folgende Wahrscheinlichkeiten:

\(P(X = 4) =\)

\(P(X > 5) =\)

\(P(4 \leq X < 5) =\)

Die Verteilungsfunktion ergibt sich als kumulative Summe der Werte aus der Wahrscheinlichkeitsfunktion \(f(x)\), d.h. \(F(x) = f(1) + \dots + f(x)\) für \(x = 1, 2, \dots, 5\).

\(x\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)
\(F(x)\)	\(0.4380\)	\(0.6569\)	\(0.8029\)	\(0.9124\)	\(1.0000\)

Damit können die drei gesuchten Wahrscheinlichkeiten berechnet werden:

\[\begin{eqnarray*} P(X = 4) & = & f(4) = \frac{60}{137} \cdot \frac{1}{4} = 0.1095\\ P(X > 5) & = & 1 - P(X \leq 5) = 1 - F(5) = 1 - 1 = 0\\ P(4 \leq X < 4) & = & P(X \leq 4) - P(X \leq 3) = F(4) - F(3) \\ & = & 0.9124 - 0.8029 = 0.1095 \end{eqnarray*}\]

Ein diskrete Zufallsvariable \(X\) hat folgende Wahrscheinlichkeitsfunktion

\[ f(x)= \left\{ \begin{array}{cc} \frac{280}{761} \cdot \frac{1}{x} & x = 1, 2, \dots, 8 \\ 0 & \mbox{sonst} \end{array} \right. \]

Berechnen Sie die Verteilungsfunktion \(F(x)\).

\(x\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)
\(F(x)\)

Berechnen Sie folgende Wahrscheinlichkeiten:

\(P(X = 5) =\)

\(P(X \geq 7) =\)

\(P(5 \leq X < 7) =\)

Die Verteilungsfunktion ergibt sich als kumulative Summe der Werte aus der Wahrscheinlichkeitsfunktion \(f(x)\), d.h. \(F(x) = f(1) + \dots + f(x)\) für \(x = 1, 2, \dots, 8\).

\(x\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)	\(8\)
\(F(x)\)	\(0.3679\)	\(0.5519\)	\(0.6746\)	\(0.7665\)	\(0.8401\)	\(0.9014\)	\(0.9540\)	\(1.0000\)

Damit können die drei gesuchten Wahrscheinlichkeiten berechnet werden:

\[\begin{eqnarray*} P(X = 5) & = & f(5) = \frac{280}{761} \cdot \frac{1}{5} = 0.0736\\ P(X \geq 7) & = & 1 - P(X \leq 6) = 1 - F(6) = 1 - 0.9014 = 0.0986\\ P(5 \leq X < 5) & = & P(X \leq 6) - P(X \leq 4) = F(6) - F(4) \\ & = & 0.9014 - 0.7665 = 0.1349 \end{eqnarray*}\]

Bedingte Wahrscheinlichkeiten

a

Ein Basketballspieler erhält zwei Freiwürfe. Aus langer Beobachtung weiß er, dass er mit \(63\%\) Wahrscheinlichkeit beim ersten Wurf trifft. Die gleiche Trefferquote gilt auch für den zweiten Wurf. Die Wahrscheinlichkeit für zwei Treffer unmittelbar hintereinander liegt bei \(40.32\%\).

Wie groß ist die Wahrscheinlichkeit, dass der Spieler beim zweiten Wurf nicht trifft, wenn er beim ersten Wurf getroffen hat? (Geben Sie das Ergebnis in Prozent an.)

Bezeichne \(A\) das Ereignis Treffer im ersten Wurf und \(B\) das Ereignis Treffer im zweiten Wurf. Dann ist \(P(A) = P(B) = 0.63\) und \(P(A \cap B) = 0.4032\). Damit läßt sich die Vierfeldertafel aufstellen:

	\(~B~\)	\(~\overline{B}~\)
\(~A~\)	\(~0.4032~\)	\(~0.2268~\)	\(~0.63~\)
\(~\overline{A}~\)	\(~0.2268~\)	\(~0.1432~\)	\(~0.37~\)
	\(~0.63~\)	\(~0.37~\)	\(~1~\)

Gefragt ist nach \[\begin{aligned} P(\overline{B} | {A}) = \frac{P({A} \cap \overline{B})}{P({A})} = \frac{0.2268}{0.63} = 0.36 \end{aligned}\] Die Wahrscheinlichkeit, dass der Spieler beim zweiten Wurf nicht trifft, wenn er beim ersten Wurf getroffen hat, beträgt somit \(36.00 \%\).

Ein Basketballspieler erhält zwei Freiwürfe. Aus langer Beobachtung weiß er, dass er mit \(79\%\) Wahrscheinlichkeit beim ersten Wurf trifft. Die gleiche Trefferquote gilt auch für den zweiten Wurf. Die Wahrscheinlichkeit für zwei Treffer unmittelbar hintereinander liegt bei \(65.57\%\).

Wie groß ist die Wahrscheinlichkeit, dass der Spieler beim zweiten Wurf trifft, wenn er beim ersten Wurf getroffen hat? (Geben Sie das Ergebnis in Prozent an.)

Bezeichne \(A\) das Ereignis Treffer im ersten Wurf und \(B\) das Ereignis Treffer im zweiten Wurf. Dann ist \(P(A) = P(B) = 0.79\) und \(P(A \cap B) = 0.6557\). Damit läßt sich die Vierfeldertafel aufstellen:

	\(~B~\)	\(~\overline{B}~\)
\(~A~\)	\(~0.6557~\)	\(~0.1343~\)	\(~0.79~\)
\(~\overline{A}~\)	\(~0.1343~\)	\(~0.0757~\)	\(~0.21~\)
	\(~0.79~\)	\(~0.21~\)	\(~1~\)

Gefragt ist nach \[\begin{aligned} P({B} | {A}) = \frac{P({A} \cap {B})}{P({A})} = \frac{0.6557}{0.79} = 0.83 \end{aligned}\] Die Wahrscheinlichkeit, dass der Spieler beim zweiten Wurf trifft, wenn er beim ersten Wurf getroffen hat, beträgt somit \(83.00 \%\).

Ein Basketballspieler erhält zwei Freiwürfe. Aus langer Beobachtung weiß er, dass er mit \(80\%\) Wahrscheinlichkeit beim ersten Wurf trifft. Die gleiche Trefferquote gilt auch für den zweiten Wurf. Die Wahrscheinlichkeit für zwei Treffer unmittelbar hintereinander liegt bei \(64.8\%\).

Wie groß ist die Wahrscheinlichkeit, dass der Spieler beim zweiten Wurf nicht trifft, wenn er beim ersten Wurf nicht getroffen hat? (Geben Sie das Ergebnis in Prozent an.)

Bezeichne \(A\) das Ereignis Treffer im ersten Wurf und \(B\) das Ereignis Treffer im zweiten Wurf. Dann ist \(P(A) = P(B) = 0.8\) und \(P(A \cap B) = 0.648\). Damit läßt sich die Vierfeldertafel aufstellen:

	\(~B~\)	\(~\overline{B}~\)
\(~A~\)	\(~0.648~\)	\(~0.152~\)	\(~0.8~\)
\(~\overline{A}~\)	\(~0.152~\)	\(~0.048~\)	\(~0.2~\)
	\(~0.8~\)	\(~0.2~\)	\(~1~\)

Gefragt ist nach \[\begin{aligned} P(\overline{B} | \overline{A}) = \frac{P(\overline{A} \cap \overline{B})}{P(\overline{A})} = \frac{0.048}{0.2} = 0.24 \end{aligned}\] Die Wahrscheinlichkeit, dass der Spieler beim zweiten Wurf nicht trifft, wenn er beim ersten Wurf nicht getroffen hat, beträgt somit \(24.00 \%\).

b

Die Europäische Lawinen-Warnskala hat fünf Stufen, wobei ab Stufe drei ausdrücklich vor einem Lawinenabgang gewarnt wird. Die durchschnittliche Wahrscheinlichkeit für einen Lawinenabgang auf Ihrer Lieblingstour beträgt \(4\%\). Wenn eine Lawine abgeht, wurde mit einer Wahrscheinlichkeit von \(68\%\) korrekt auf die Gefahr hingewiesen. Geht keine Lawine ab, wurde mit einer Wahrscheinlichkeit von \(85\%\) auch vor keiner gewarnt.

Es wird vor einer Lawine gewarnt. Mit welcher Wahrscheinlichkeit geht am selben Tag tatsächlich eine Lawine ab? (Geben Sie das Ergebnis in Prozent an.)

Bezeichnen wir \(L\) als das Ereignis Lawinenabgang und \(W\) als das Ereignis Warnung. Somit lässt sich die folgende Vierfeldertafel aufstellen:

	\(~L~\)	\(~\overline{L}~\)
\(~W~\)	\(~0.0272~\)	\(~0.144~\)	\(~0.1712~\)
\(~\overline{W}~\)	\(~0.0128~\)	\(~0.816~\)	\(~0.8288~\)
	\(~0.04~\)	\(~0.96~\)	\(~1~\)

Gesucht ist die bedingte Wahrscheinlichkeit \[\begin{aligned} P(L | W)= \frac{P(L \cap W)}{P(W)} = \frac{0.0272}{0.1712} = 0.158879 \end{aligned}\] Die Wahrscheinlichkeit, dass an einem Tag mit Lawinenwarnung tatsächlich eine Lawine abgeht, beträgt somit \(15.89 \%\).

Die Europäische Lawinen-Warnskala hat fünf Stufen, wobei ab Stufe drei ausdrücklich vor einem Lawinenabgang gewarnt wird. Die durchschnittliche Wahrscheinlichkeit für einen Lawinenabgang auf Ihrer Lieblingstour beträgt \(8\%\). Wenn eine Lawine abgeht, wurde mit einer Wahrscheinlichkeit von \(66\%\) korrekt auf die Gefahr hingewiesen. Geht keine Lawine ab, wurde mit einer Wahrscheinlichkeit von \(94\%\) auch vor keiner gewarnt.

Es wird vor einer Lawine gewarnt. Mit welcher Wahrscheinlichkeit geht am selben Tag dennoch keine Lawine ab? (Geben Sie das Ergebnis in Prozent an.)

Bezeichnen wir \(L\) als das Ereignis Lawinenabgang und \(W\) als das Ereignis Warnung. Somit lässt sich die folgende Vierfeldertafel aufstellen:

	\(~L~\)	\(~\overline{L}~\)
\(~W~\)	\(~0.0528~\)	\(~0.0552~\)	\(~0.108~\)
\(~\overline{W}~\)	\(~0.0272~\)	\(~0.8648~\)	\(~0.892~\)
	\(~0.08~\)	\(~0.92~\)	\(~1~\)

Gesucht ist die bedingte Wahrscheinlichkeit \[\begin{aligned} P(\overline{L} | W)= \frac{P(\overline{L} \cap W)}{P(W)} = \frac{0.0552}{0.108} = 0.511111 \end{aligned}\] Die Wahrscheinlichkeit, dass an einem Tag mit Lawinenwarnung dennoch keine Lawine abgeht, beträgt somit \(51.11 \%\).

Die Europäische Lawinen-Warnskala hat fünf Stufen, wobei ab Stufe drei ausdrücklich vor einem Lawinenabgang gewarnt wird. Die durchschnittliche Wahrscheinlichkeit für einen Lawinenabgang auf Ihrer Lieblingstour beträgt \(7\%\). Wenn eine Lawine abgeht, wurde mit einer Wahrscheinlichkeit von \(62\%\) korrekt auf die Gefahr hingewiesen. Geht keine Lawine ab, wurde mit einer Wahrscheinlichkeit von \(92\%\) auch vor keiner gewarnt.

Mit welcher Wahrscheinlichkeit wurde nicht davor gewarnt, wenn eine Lawine abgeht? (Geben Sie das Ergebnis in Prozent an.)

Bezeichnen wir \(L\) als das Ereignis Lawinenabgang und \(W\) als das Ereignis Warnung. Somit lässt sich die folgende Vierfeldertafel aufstellen:

	\(~L~\)	\(~\overline{L}~\)
\(~W~\)	\(~0.0434~\)	\(~0.0744~\)	\(~0.1178~\)
\(~\overline{W}~\)	\(~0.0266~\)	\(~0.8556~\)	\(~0.8822~\)
	\(~0.07~\)	\(~0.93~\)	\(~1~\)

Gesucht ist die bedingte Wahrscheinlichkeit \[\begin{aligned} P(\overline{W} | L)= \frac{P(\overline{W} \cap L)}{P(L)} = \frac{0.0266}{0.07} = 0.38 \end{aligned}\] Die Wahrscheinlichkeit, dass es keine Lawinenwarnung gab, wenn am gleichen Tag noch eine Lawine abgeht, beträgt somit \(38.00 \%\).

c

Eine Umfrage ergab, dass \(21\%\) aller Studierenden männlichen Geschlechts sind und rauchen. \(41\%\) aller Studierenden rauchen. \(67\%\) aller Nichtraucher unter den Studierenden sind weiblich.

Wie groß ist die Wahrscheinlichkeit, dass ein Nichtraucher männlichen Geschlechts ist? (Geben Sie das Ergebnis in Prozent an.)

Bezeichne \(W\) das Ereignis Studierende weiblichen Geschlechts und \(R\) das Ereignis Rauchen.
Die fehlende Wahrscheinlichkeit \(P(W \cap \overline{R})\) lässt sich berechnen durch \(P(W | \overline{R}) \cdot P(\overline{R}) = {0.67} \cdot {0.59} = 0.3953\).
Somit läßt sich folgende Vierfeldertafel aufstellen:

	\(~R~\)	\(~\overline{R}~\)
\(~W~\)	\(~0.2~\)	\(~0.3953~\)	\(~0.5953~\)
\(~\overline{W}~\)	\(~0.21~\)	\(~0.1947~\)	\(~0.4047~\)
	\(~0.41~\)	\(~0.59~\)	\(~1~\)

Gesucht ist die bedingte Wahrscheinlichkeit \[\begin{aligned} P(\overline{W} | \overline{R})= \frac{P(\overline{W} \cap \overline{R})}{P(\overline{R})}= \frac{0.1947}{0.59} = 0.33 \end{aligned}\] Die Wahrscheinlichkeit, dass ein Nichtraucher männlichen Geschlechts ist, beträgt somit \(33.00 \%\).

Eine Umfrage ergab, dass \(25\%\) aller Studierenden männlichen Geschlechts sind und rauchen. \(41\%\) aller Studierenden rauchen. \(67\%\) aller Nichtraucher unter den Studierenden sind weiblich.

Wie groß ist die Wahrscheinlichkeit, dass eine Studentin raucht? (Geben Sie das Ergebnis in Prozent an.)

Bezeichne \(W\) das Ereignis Studierende weiblichen Geschlechts und \(R\) das Ereignis Rauchen.
Die fehlende Wahrscheinlichkeit \(P(W \cap \overline{R})\) lässt sich berechnen durch \(P(W | \overline{R}) \cdot P(\overline{R}) = {0.67} \cdot {0.59} = 0.3953\).
Somit läßt sich folgende Vierfeldertafel aufstellen:

	\(~R~\)	\(~\overline{R}~\)
\(~W~\)	\(~0.16~\)	\(~0.3953~\)	\(~0.5553~\)
\(~\overline{W}~\)	\(~0.25~\)	\(~0.1947~\)	\(~0.4447~\)
	\(~0.41~\)	\(~0.59~\)	\(~1~\)

Gesucht ist die bedingte Wahrscheinlichkeit \[\begin{aligned} P(R | W) = \frac{P(W \cap R)}{P(W)} = \frac{0.16}{0.5553} = 0.288133 \end{aligned}\] Die Wahrscheinlichkeit, dass eine Studentin raucht, beträgt somit \(28.81 \%\).

Eine Umfrage ergab, dass \(29\%\) aller Studierenden männlichen Geschlechts sind und rauchen. \(41\%\) aller Studierenden rauchen. \(66\%\) aller Nichtraucher unter den Studierenden sind weiblich.

Wie groß ist die Wahrscheinlichkeit, dass eine Studentin nicht raucht? (Geben Sie das Ergebnis in Prozent an.)

Bezeichne \(W\) das Ereignis Studierende weiblichen Geschlechts und \(R\) das Ereignis Rauchen.
Die fehlende Wahrscheinlichkeit \(P(W \cap \overline{R})\) lässt sich berechnen durch \(P(W | \overline{R}) \cdot P(\overline{R}) = {0.66} \cdot {0.59} = 0.3894\).
Somit läßt sich folgende Vierfeldertafel aufstellen:

	\(~R~\)	\(~\overline{R}~\)
\(~W~\)	\(~0.12~\)	\(~0.3894~\)	\(~0.5094~\)
\(~\overline{W}~\)	\(~0.29~\)	\(~0.2006~\)	\(~0.4906~\)
	\(~0.41~\)	\(~0.59~\)	\(~1~\)

Gesucht ist die bedingte Wahrscheinlichkeit \[\begin{aligned} P(\overline{R} | W) = \frac{P(W \cap \overline{R})}{P(W)} = \frac{0.3894}{0.5094} = 0.764429 \end{aligned}\] Die Wahrscheinlichkeit, dass ein Studentin nicht raucht, beträgt somit \(76.44 \%\).

d

Eine Studierende beschließt, sich bei zwei verschiedenen Unternehmen für ein Praktikum zu bewerben. Sie hat ein wenig recherchiert und geht davon aus, dass Unternehmen A ihr mit einer Wahrscheinlichkeit von \(23\%\) einen Praktikumsplatz anbietet. Unabhängig davon wird Unternehmen B ihr mit einer Wahrscheinlichkeit von \(71\%\) einen Praktikumsplatz anbieten.

Wie groß ist die Wahrscheinlichkeit, dass die Studierende genau einen Praktikumsplatz erhält? (Geben Sie das Ergebnis in Prozent an.)

Sei das Ereignis \(A\) Jobangebot von Unternehmen A und \(B\) Jobangebot von Unternehmen B. Die zwei Ereignisse sind voneinander unabhängig, wenn gilt: \[\begin{aligned} P(A) = P(A|B) \Longleftrightarrow P(A \cap B) = P(A) \cdot P(B) \end{aligned}\] Gefragt ist nach \[\begin{aligned} P(\textrm{genau einen Praktikumsplatz}) & = & 1 - P(A) \cdot P(B) - P(\overline{A}) \cdot P(\overline{B}) \\ & = & 1 - P(A) \cdot P(B) - (1 - P(A)) \cdot (1 - P(B)) \\ & = & 1 - 0.23 \cdot 0.71 - (1 - 0.23) \cdot (1 - 0.71) \\ & = & 0.6134 \end{aligned}\] Damit beträgt die Wahrscheinlichkeit, dass sie genau einen Praktikumsplatz erhält, \(61.34\%\).

Eine Studierende beschließt, sich bei zwei verschiedenen Unternehmen für ein Praktikum zu bewerben. Sie hat ein wenig recherchiert und geht davon aus, dass Unternehmen A ihr mit einer Wahrscheinlichkeit von \(90\%\) einen Praktikumsplatz anbietet. Unabhängig davon wird Unternehmen B ihr mit einer Wahrscheinlichkeit von \(79\%\) einen Praktikumsplatz anbieten.

Wie groß ist die Wahrscheinlichkeit, dass die Studierende höchstens einen Praktikumsplatz erhält? (Geben Sie das Ergebnis in Prozent an.)

Sei das Ereignis \(A\) Jobangebot von Unternehmen A und \(B\) Jobangebot von Unternehmen B. Die zwei Ereignisse sind voneinander unabhängig, wenn gilt: \[\begin{aligned} P(A) = P(A|B) \Longleftrightarrow P(A \cap B) = P(A) \cdot P(B) \end{aligned}\] Gefragt ist nach \[\begin{aligned} P(\textrm{h\"ochstens einen Praktikumsplatz}) & = & 1 - P(A) \cdot P(B) \\ & = & 1 - 0.9 \cdot 0.79 \\ & = & 0.289 \end{aligned}\] Damit beträgt die Wahrscheinlichkeit, dass sie höchstens einen Praktikumsplatz erhält, \(28.90\%\).

Eine Studierende beschließt, sich bei zwei verschiedenen Unternehmen für ein Praktikum zu bewerben. Sie hat ein wenig recherchiert und geht davon aus, dass Unternehmen A ihr mit einer Wahrscheinlichkeit von \(21\%\) einen Praktikumsplatz anbietet. Unabhängig davon wird Unternehmen B ihr mit einer Wahrscheinlichkeit von \(61\%\) einen Praktikumsplatz anbieten.

Wie groß ist die Wahrscheinlichkeit, dass die Studierende genau einen Praktikumsplatz erhält? (Geben Sie das Ergebnis in Prozent an.)

Sei das Ereignis \(A\) Jobangebot von Unternehmen A und \(B\) Jobangebot von Unternehmen B. Die zwei Ereignisse sind voneinander unabhängig, wenn gilt: \[\begin{aligned} P(A) = P(A|B) \Longleftrightarrow P(A \cap B) = P(A) \cdot P(B) \end{aligned}\] Gefragt ist nach \[\begin{aligned} P(\textrm{genau einen Praktikumsplatz}) & = & 1 - P(A) \cdot P(B) - P(\overline{A}) \cdot P(\overline{B}) \\ & = & 1 - P(A) \cdot P(B) - (1 - P(A)) \cdot (1 - P(B)) \\ & = & 1 - 0.21 \cdot 0.61 - (1 - 0.21) \cdot (1 - 0.61) \\ & = & 0.5638 \end{aligned}\] Damit beträgt die Wahrscheinlichkeit, dass sie genau einen Praktikumsplatz erhält, \(56.38\%\).

Erwartungswert und Varianz

a

Die Zufallsvariable \(X\) hat eine stückweise konstante Dichtefunktion \(f\).

Diese ist nachfolgend gegeben durch ihren Graphen.

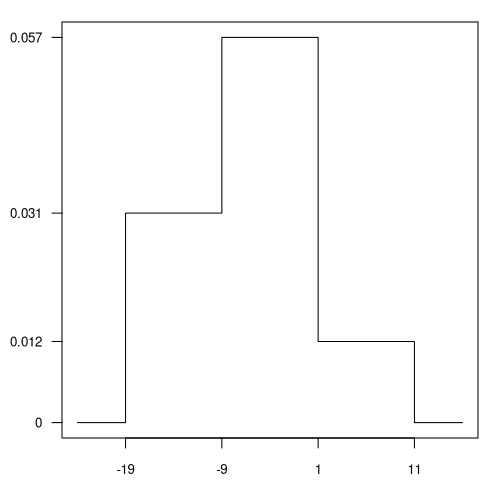
Berechnen Sie die Wahrscheinlichkeit \(P(X > -7)\). (Geben Sie das Ergebnis in Prozent an.)

Die Wahrscheinlichkeit \(P(X > -7)\) entspricht der in der folgenden Grafik eingezeichneten Fläche unter der Dichtefunktion \(f\).

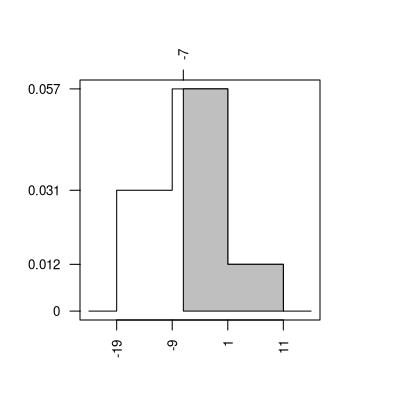
Somit ergibt sich \(P(X > -7) = 0.576 \approx 57.60\%\).

Die Zufallsvariable \(X\) hat eine stückweise konstante Dichtefunktion \(f\).

Diese ist nachfolgend gegeben durch ihren Graphen.

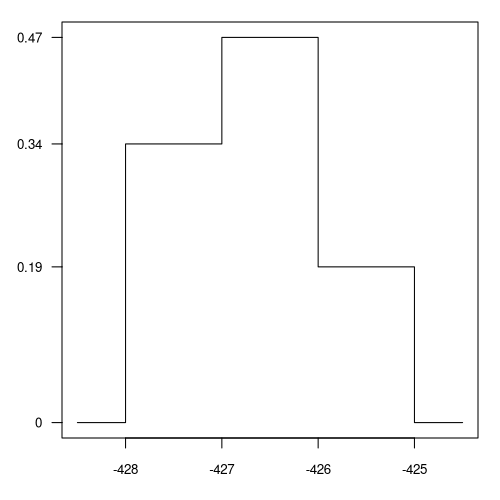
Berechnen Sie die Wahrscheinlichkeit \(P(-427.5 < X < -426.7)\). (Geben Sie das Ergebnis in Prozent an.)

Die Wahrscheinlichkeit \(P(-427.5 < X < -426.7)\) entspricht der in der folgenden Grafik eingezeichneten Fläche unter der Dichtefunktion \(f\).

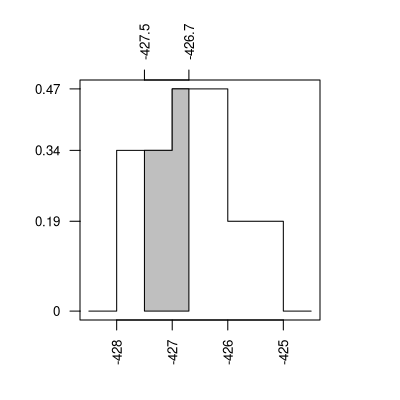
Somit ergibt sich \(P(-427.5 < X < -426.7) = 0.311 \approx 31.10\%\).

Die Zufallsvariable \(X\) hat eine stückweise konstante Dichtefunktion \(f\).

Diese ist nachfolgend gegeben durch ihren Graphen.

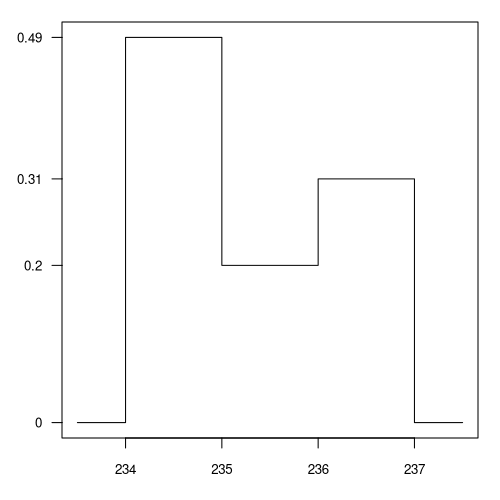
Berechnen Sie die Wahrscheinlichkeit \(P(X > 235.8)\). (Geben Sie das Ergebnis in Prozent an.)

Die Wahrscheinlichkeit \(P(X > 235.8)\) entspricht der in der folgenden Grafik eingezeichneten Fläche unter der Dichtefunktion \(f\).

Somit ergibt sich \(P(X > 235.8) = 0.35 \approx 35.00\%\).

b

Die Fahrzeit in Minuten zur Uni sei exponentialverteilt mit durchschnittlicher Fahrzeit \(\mu = 15\) Minuten. Die Verteilungsfunktion \(F(x)\) ist gegeben durch \[F(x) = \left\{ \begin{array}{ll} 0 & x < 0 \\ 1 - \exp \left(-\frac{1}{\mu}x \right) & x \geq 0 \\ \end{array} \right.\]

Berechnen Sie die Wahrscheinlichkeit (in Prozent) für eine Fahrzeit kleiner oder gleich \(15\) Minuten.

\[\begin{aligned} P(\mbox{Fahrzeit kleiner gleich 15 Min.}) &=& P(X \leq 15) \\ &=& F(15) \\ &=& 1 - \exp \left ( - \frac{1}{15} 15 \right ) \\ &=& 0.632121 \end{aligned}\]

Die Wahrscheinlichkeit beträgt somit \(63.21\%\).

Die Fahrzeit in Minuten zur Uni sei exponentialverteilt mit durchschnittlicher Fahrzeit \(\mu = 23\) Minuten. Die Verteilungsfunktion \(F(x)\) ist gegeben durch \[F(x) = \left\{ \begin{array}{ll} 0 & x < 0 \\ 1 - \exp \left(-\frac{1}{\mu}x \right) & x \geq 0 \\ \end{array} \right.\]

Berechnen Sie die Wahrscheinlichkeit (in Prozent) für eine Fahrzeit zwischen \(7\) und \(21\) Minuten.

\[\begin{aligned} P(\mbox{Fahrzeit zw. 7 u. 21 Min.}) &=& P(7 \leq X \leq 21) \\ &=& P(X \leq 21) - P(X \leq 7) \\ &=& F(21) - F(7) \\ &=& \left [ 1 - \exp \left ( - \frac{1}{23} 21 \right ) \right ] - \left [ 1 - \mbox{exp} \left ( - \frac{1}{23} 7 \right ) \right ] \\ &=& 0.336303 \end{aligned}\]

Die Wahrscheinlichkeit beträgt somit \(33.63\%\).

Die Fahrzeit in Minuten zur Uni sei exponentialverteilt mit durchschnittlicher Fahrzeit \(\mu = 15\) Minuten. Die Verteilungsfunktion \(F(x)\) ist gegeben durch \[F(x) = \left\{ \begin{array}{ll} 0 & x < 0 \\ 1 - \exp \left(-\frac{1}{\mu}x \right) & x \geq 0 \\ \end{array} \right.\]

Berechnen Sie die Wahrscheinlichkeit (in Prozent) für eine Fahrzeit zwischen \(15\) und \(31\) Minuten.

\[\begin{aligned} P(\mbox{Fahrzeit zw. 15 u. 31 Min.}) &=& P(15 \leq X \leq 31) \\ &=& P(X \leq 31) - P(X \leq 15) \\ &=& F(31) - F(15) \\ &=& \left [ 1 - \exp \left ( - \frac{1}{15} 31 \right ) \right ] - \left [ 1 - \mbox{exp} \left ( - \frac{1}{15} 15 \right ) \right ] \\ &=& 0.241272 \end{aligned}\]

Die Wahrscheinlichkeit beträgt somit \(24.13\%\).

c

Gegeben ist folgende stückweise konstante Dichtefunktion der Zufallsvariablen \(X\): \[\begin{aligned} f(x) = \left\{\begin{array}{lcl} 0.22 & & 6 \leq x < 8\\0.13 & & 8 \leq x < 10\\0.04 & \mbox{f\"ur} & 10 \leq x < 13 \\ 0.03 && 13 \leq x \leq 19 \\ 0 && \mathrm{sonst.} \end{array}\right. \end{aligned}\] Berechnen Sie den Erwartungswert \(E(X)\).

Der Erwartungswert einer stückweise konstanten Dichtefunktion ist das gewichtete Mittel der jeweiligen Intervallmitten mit den Wahrscheinlichkeiten im Intervall: \[\begin{aligned} E(X) &=& 0.22 \cdot (8 - 6) \cdot \frac{6 + 8}{2} + \ldots + 0.03 \cdot (19 - 13) \cdot \frac{13 + 19}{2} \\ &=& 0.44 \cdot 7 + 0.26 \cdot 9 + 0.12 \cdot 11.5 + 0.18 \cdot 16 \\ &=& 9.68 \end{aligned}\]

Gegeben ist folgende stückweise konstante Dichtefunktion der Zufallsvariablen \(X\): \[\begin{aligned} f(x) = \left\{\begin{array}{lcl} 0.2 & & 8 \leq x < 11\\0.05 & & 11 \leq x < 15\\0.03 & \mbox{f\"ur} & 15 \leq x < 17 \\ 0.14 && 17 \leq x \leq 18 \\ 0 && \mathrm{sonst.} \end{array}\right. \end{aligned}\] Berechnen Sie den Erwartungswert \(E(X)\).

Der Erwartungswert einer stückweise konstanten Dichtefunktion ist das gewichtete Mittel der jeweiligen Intervallmitten mit den Wahrscheinlichkeiten im Intervall: \[\begin{aligned} E(X) &=& 0.2 \cdot (11 - 8) \cdot \frac{8 + 11}{2} + \ldots + 0.14 \cdot (18 - 17) \cdot \frac{17 + 18}{2} \\ &=& 0.6 \cdot 9.5 + 0.2 \cdot 13 + 0.06 \cdot 16 + 0.14 \cdot 17.5 \\ &=& 11.71 \end{aligned}\]

Gegeben ist folgende stückweise konstante Dichtefunktion der Zufallsvariablen \(X\): \[\begin{aligned} f(x) = \left\{\begin{array}{lcl} 0.21 & & 3 \leq x < 6\\0.01 & \mbox{f\"ur} & 6 \leq x < 7 \\ 0.09 && 7 \leq x \leq 11 \\ 0 && \mathrm{sonst.} \end{array}\right. \end{aligned}\] Berechnen Sie den Erwartungswert \(E(X)\).

Der Erwartungswert einer stückweise konstanten Dichtefunktion ist das gewichtete Mittel der jeweiligen Intervallmitten mit den Wahrscheinlichkeiten im Intervall: \[\begin{aligned} E(X) &=& 0.21 \cdot (6 - 3) \cdot \frac{3 + 6}{2} + \ldots + 0.09 \cdot (11 - 7) \cdot \frac{7 + 11}{2} \\ &=& 0.63 \cdot 4.5 + 0.01 \cdot 6.5 + 0.36 \cdot 9 \\ &=& 6.14 \end{aligned}\]

d

Ein Teilnehmer einer Spielshow im Fernsehen hat die Wahl zwischen zwei Möglichkeiten: Einstreichen eines sicheren Gewinns von \(207\) Euro oder Teilnahme an einem Glücksspiel. Der Gewinn des Glücksspiels wird durch die Zufallsvariable \(G\) beschrieben. Diese hat folgende Wahrscheinlichkeitsfunktion:

\(g\)	\(30\)	\(160\)	\(210\)	\(220\)	\(400\)
\(P(G = g)\)	\(0.32\)	\(0.16\)	\(0.09\)	\(0.31\)	\(0.12\)

Nach der Erwartungsnutzentheorie entscheidet sich der Teilnehmer so zwischen den beiden Möglichkeiten, dass der erwartete Nutzen maximiert wird. Berechnen Sie den erwarteten Nutzen, den der Teilnehmer nach seiner Entscheidung erzielt, wenn die Nutzenfunktion \(U(g) = \sqrt g\) vorliegt.

Die Nutzenfunktion \(U(G)\) ist eine nichtlineare Transformation der diskreten Zufallsvariable \(G\) mit möglichen Werten \(g_1, \ldots , g_k\). Der erwartete Nutzen des Glücksspiels ist daher gegeben durch \[\begin{aligned} E(U(G)) & = & U(g_1) \cdot P(G = g_1) + \ldots + U(g_k) \cdot P(G = g_k) \\ & = & \sqrt{30} \cdot P(G = 30) + \sqrt{160} \cdot P(G = 160) + \sqrt{210} \cdot P(G = 210)\\ && + \sqrt{220} \cdot P(G = 220) + \sqrt{400} \cdot P(G = 400)\\ & = & 5.4772 \cdot 0.32 + 12.6491 \cdot 0.16 + 14.4914 \cdot 0.09 + 14.8324 \cdot 0.31 + 20.0000 \cdot 0.12\\ & = & 12.0788. \end{aligned}\] Der erwartete Nutzen des Glücksspiels beträgt somit \(12.08\).

Der (erwartete) Nutzen des sicheren Gewinns beträgt \(\sqrt{ 207 } = 14.39\).

Da der erwartete Nutzen des Glücksspiels mit \(12.08\) kleiner ist als der Nutzen des sicheren Gewinns, entscheidet sich der Teilnehmer für den sicheren Gewinn und erzielt damit einen erwarteten Nutzen von \(14.39\).

Ein Teilnehmer einer Spielshow im Fernsehen hat die Wahl zwischen zwei Möglichkeiten: Einstreichen eines sicheren Gewinns von \(280\) Euro oder Teilnahme an einem Glücksspiel. Der Gewinn des Glücksspiels wird durch die Zufallsvariable \(G\) beschrieben. Diese hat folgende Wahrscheinlichkeitsfunktion:

\(g\)	\(20\)	\(210\)	\(300\)	\(350\)	\(370\)
\(P(G = g)\)	\(0.30\)	\(0.20\)	\(0.05\)	\(0.30\)	\(0.15\)

Nach der Erwartungsnutzentheorie entscheidet sich der Teilnehmer so zwischen den beiden Möglichkeiten, dass der erwartete Nutzen maximiert wird. Berechnen Sie den erwarteten Nutzen, den der Teilnehmer nach seiner Entscheidung erzielt, wenn die Nutzenfunktion \(U(g) = \ln(g)\) vorliegt.

Die Nutzenfunktion \(U(G)\) ist eine nichtlineare Transformation der diskreten Zufallsvariable \(G\) mit möglichen Werten \(g_1, \ldots , g_k\). Der erwartete Nutzen des Glücksspiels ist daher gegeben durch \[\begin{aligned} E(U(G)) & = & U(g_1) \cdot P(G = g_1) + \ldots + U(g_k) \cdot P(G = g_k) \\ & = & \ln(20) \cdot P(G = 20) + \ln(210) \cdot P(G = 210) + \ln(300) \cdot P(G = 300)\\ && + \ln(350) \cdot P(G = 350) + \ln(370) \cdot P(G = 370)\\ & = & 2.9957 \cdot 0.30 + 5.3471 \cdot 0.20 + 5.7038 \cdot 0.05 + 5.8579 \cdot 0.30 + 5.9135 \cdot 0.15\\ & = & 4.8977. \end{aligned}\] Der erwartete Nutzen des Glücksspiels beträgt somit \(4.90\).

Der (erwartete) Nutzen des sicheren Gewinns beträgt \(\ln( 280 ) = 5.63\).

Da der erwartete Nutzen des Glücksspiels mit \(4.90\) kleiner ist als der Nutzen des sicheren Gewinns, entscheidet sich der Teilnehmer für den sicheren Gewinn und erzielt damit einen erwarteten Nutzen von \(5.63\).

Ein Teilnehmer einer Spielshow im Fernsehen hat die Wahl zwischen zwei Möglichkeiten: Einstreichen eines sicheren Gewinns von \(120\) Euro oder Teilnahme an einem Glücksspiel. Der Gewinn des Glücksspiels wird durch die Zufallsvariable \(G\) beschrieben. Diese hat folgende Wahrscheinlichkeitsfunktion:

\(g\)	\(10\)	\(60\)	\(100\)	\(210\)	\(390\)
\(P(G = g)\)	\(0.06\)	\(0.12\)	\(0.34\)	\(0.41\)	\(0.07\)

Nach der Erwartungsnutzentheorie entscheidet sich der Teilnehmer so zwischen den beiden Möglichkeiten, dass der erwartete Nutzen maximiert wird. Berechnen Sie den erwarteten Nutzen, den der Teilnehmer nach seiner Entscheidung erzielt, wenn die Nutzenfunktion \(U(g) = \ln(g)\) vorliegt.

Die Nutzenfunktion \(U(G)\) ist eine nichtlineare Transformation der diskreten Zufallsvariable \(G\) mit möglichen Werten \(g_1, \ldots , g_k\). Der erwartete Nutzen des Glücksspiels ist daher gegeben durch \[\begin{aligned} E(U(G)) & = & U(g_1) \cdot P(G = g_1) + \ldots + U(g_k) \cdot P(G = g_k) \\ & = & \ln(10) \cdot P(G = 10) + \ln(60) \cdot P(G = 60) + \ln(100) \cdot P(G = 100)\\ && + \ln(210) \cdot P(G = 210) + \ln(390) \cdot P(G = 390)\\ & = & 2.3026 \cdot 0.06 + 4.0943 \cdot 0.12 + 4.6052 \cdot 0.34 + 5.3471 \cdot 0.41 + 5.9661 \cdot 0.07\\ & = & 4.8052. \end{aligned}\] Der erwartete Nutzen des Glücksspiels beträgt somit \(4.81\).

Der (erwartete) Nutzen des sicheren Gewinns beträgt \(\ln( 120 ) = 4.79\).

Da der erwartete Nutzen des Glücksspiels mit \(4.81\) größer ist als der Nutzen des sicheren Gewinns, entscheidet sich der Teilnehmer für das Glücksspiel und erzielt damit einen erwarteten Nutzen von \(4.81\).

e

Ein Maschinenbauunternehmen stellt Großanlagen eines bestimmten Typs her. Die Wahrscheinlichkeiten dafür, dass im nächsten Geschäftsjahr bestimmte Anzahlen von Anlagen abgesetzt werden können, haben folgende Werte:

Anlagenzahl	\(0\)	\(1\)	\(2\)	\(3\)
Wahrscheinlichkeit	\(0.21\)	\(0.23\)	\(0.39\)	\(0.17\)

Die Kosten des Unternehmens belaufen sich auf Fixkosten von \(116\) GE und variable Kosten von \(37\) GE je gebauter Anlage. Der Erlös pro abgesetzter Anlage beträgt \(182\) GE.

Berechnen Sie die Standardabweichung des Gewinns (bzw. Verlusts) für das kommende Geschäftsjahr.

Der Gewinn (bzw. Verlust) \(G\) ergibt sich aus dem Deckungsbeitrag, der Anzahl verkaufter Anlagen \(A\) und den Fixkosten: \(G = (182 - 37) \cdot A - 116\).

Für die Ermittlung der Standardabweichung des Gewinns benötigt man also Erwartungswert und Varianz für die Anzahl Anlagen: \[\begin{aligned} E(A) & = & 0 \cdot 0.21 + 1 \cdot 0.23 + 2 \cdot 0.39 + 3 \cdot 0.17\\ & = & 1.52 \\ V(A) & = & \left(0^2 \cdot 0.21 + 1^2 \cdot 0.23 + 2^2 \cdot 0.39 + 3^2 \cdot 0.17\right) - 1.52^2 \\ & = & 1.0096 \\ V(G) & = & V((182 - 37) \cdot A - 116) \\ & = & (182 - 37)^2 \cdot V(A) \\ & = & 21226.84 \\ \sigma(G) & = & \sqrt{V(G)} = \sqrt{21226.84} \\ & \approx & 145.69 \ \end{aligned}\] Die Standardabweichung des Gewinns (bzw. Verlusts) beträgt also \(145.69\).

Ein Maschinenbauunternehmen stellt Großanlagen eines bestimmten Typs her. Die Wahrscheinlichkeiten dafür, dass im nächsten Geschäftsjahr bestimmte Anzahlen von Anlagen abgesetzt werden können, haben folgende Werte:

Anlagenzahl	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)
Wahrscheinlichkeit	\(0.27\)	\(0.23\)	\(0.03\)	\(0.17\)	\(0.3\)

Die Kosten des Unternehmens belaufen sich auf Fixkosten von \(101\) GE und variable Kosten von \(46\) GE je gebauter Anlage. Der Erlös pro abgesetzter Anlage beträgt \(96\) GE.

Berechnen Sie die Varianz des Gewinns (bzw. Verlusts) für das kommende Geschäftsjahr.

Der Gewinn (bzw. Verlust) \(G\) ergibt sich aus dem Deckungsbeitrag, der Anzahl verkaufter Anlagen \(A\) und den Fixkosten: \(G = (96 - 46) \cdot A - 101\).

Für die Ermittlung der Varianz des Gewinns benötigt man also Erwartungswert und Varianz für die Anzahl Anlagen: \[\begin{aligned} E(A) & = & 0 \cdot 0.27 + 1 \cdot 0.23 + 2 \cdot 0.03 + 3 \cdot 0.17 + 4 \cdot 0.3\\ & = & 2 \\ V(A) & = & \left(0^2 \cdot 0.27 + 1^2 \cdot 0.23 + 2^2 \cdot 0.03 + 3^2 \cdot 0.17 + 4^2 \cdot 0.3\right) - 2^2 \\ & = & 2.68 \\ V(G) & = & V((96 - 46) \cdot A - 101) \\ & = & (96 - 46)^2 \cdot V(A) \\ & = & 6700 % \\ % \sigma(G) & = & \sqrt{V(G)} = \sqrt{6700} \\ % & \approx & 6700.00 \ \end{aligned}\] Die Varianz des Gewinns (bzw. Verlusts) beträgt also \(6700.00\).

Ein Maschinenbauunternehmen stellt Großanlagen eines bestimmten Typs her. Die Wahrscheinlichkeiten dafür, dass im nächsten Geschäftsjahr bestimmte Anzahlen von Anlagen abgesetzt werden können, haben folgende Werte:

Anlagenzahl	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)
Wahrscheinlichkeit	\(0.05\)	\(0.34\)	\(0.19\)	\(0.08\)	\(0.34\)

Die Kosten des Unternehmens belaufen sich auf Fixkosten von \(88\) GE und variable Kosten von \(46\) GE je gebauter Anlage. Der Erlös pro abgesetzter Anlage beträgt \(184\) GE.

Berechnen Sie die Varianz des Gewinns (bzw. Verlusts) für das kommende Geschäftsjahr.

Der Gewinn (bzw. Verlust) \(G\) ergibt sich aus dem Deckungsbeitrag, der Anzahl verkaufter Anlagen \(A\) und den Fixkosten: \(G = (184 - 46) \cdot A - 88\).

Für die Ermittlung der Varianz des Gewinns benötigt man also Erwartungswert und Varianz für die Anzahl Anlagen: \[\begin{aligned} E(A) & = & 0 \cdot 0.05 + 1 \cdot 0.34 + 2 \cdot 0.19 + 3 \cdot 0.08 + 4 \cdot 0.34\\ & = & 2.32 \\ V(A) & = & \left(0^2 \cdot 0.05 + 1^2 \cdot 0.34 + 2^2 \cdot 0.19 + 3^2 \cdot 0.08 + 4^2 \cdot 0.34\right) - 2.32^2 \\ & = & 1.8776 \\ V(G) & = & V((184 - 46) \cdot A - 88) \\ & = & (184 - 46)^2 \cdot V(A) \\ & = & 35757.0144 % \\ % \sigma(G) & = & \sqrt{V(G)} = \sqrt{35757.0144} \\ % & \approx & 35757.01 \ \end{aligned}\] Die Varianz des Gewinns (bzw. Verlusts) beträgt also \(35757.01\).

f

Ein Teilnehmer einer Spielshow im Fernsehen hat die Wahl zwischen zwei Möglichkeiten: Einstreichen eines sicheren Gewinns von \(75\) Euro oder Teilnahme an einem Glücksspiel. Der Gewinn des Glücksspiels wird durch die Zufallsvariable \(G\) beschrieben. Diese hat folgende Wahrscheinlichkeitsfunktion:

\(g\)	\(50\)	\(80\)	\(180\)	\(190\)	\(380\)
\(P(G = g)\)	\(0.08\)	\(0.20\)	\(0.33\)	\(0.33\)	\(0.06\)

Nehmen Sie an, der Teilnehmer hat eine von dem Erwartungswert \(\mu\) und der Standardabweichung \(\sigma\) des Gewinns abhängige Präferenzfunktion \(h(\mu, \sigma)\):
\[h(\mu, \sigma) = \left\{ \begin{array}{ll} \mu + \sigma & \mbox{risikofreudiger Teilnehmer,} \\ \mu & \mbox{risikoneutraler Teilnehmer,} \\ \mu - \sigma & \mbox{risikoaverser Teilnehmer.} \end{array} \right.\]

Nach der Präferenztheorie entscheidet sich der Teilnehmer so zwischen den beiden Möglichkeiten, dass der Wert der Präferenzfunktion maximiert wird. Berechnen Sie den Wert der Präferenzfunktion, den ein risikoaverser Teilnehmer nach seiner Entscheidung erzielt.

Bei dem Glücksspiel berechnet sich der erwartete Gewinn durch: \[\begin{aligned} E(G) &=& 50 \cdot P(G = 50) + 80 \cdot P(G = 80) + 180 \cdot P(G = 180) + 190 \cdot P(G = 190) + 380 \cdot P(G = 380) \\ &=& 50 \cdot 0.08 + 80 \cdot 0.20 + 180 \cdot 0.33 + 190 \cdot 0.33 + 380 \cdot 0.06 \\ &=& 164.90. \end{aligned}\] Die Standardabweichung des Glücksspiels ergibt sich durch: \[\begin{aligned} E(G^2) &=& 50^2 \cdot P(G = 50) + 80^2 \cdot P(G = 80) + 180^2 \cdot P(G = 180) + 190^2 \cdot P(G = 190) + 380^2 \cdot P(G = 380) \\ &=& 2500 \cdot 0.08 + 6400 \cdot 0.20 + 32400 \cdot 0.33 + 36100 \cdot 0.33 + 144400 \cdot 0.06 \\ &=& 32749 \\ V(G) &=& E(G^2) - (E(G))^2 = 32749 - 164.9^2 = 5556.99 \\ \sigma(G) &=& \sqrt{5556.99} = 74.5452. \end{aligned}\] Damit erhalten wir für das Glücksspiel einen Wert der Präferenzfunktion des risikoaversen Teilnehmers von \[h(164.90, 74.5452) \approx 90.35.\]

Der erwartete Gewinn der sicheren Auszahlung entspricht genau dem dabei erhaltenen Betrag, also \(75.00\). Die Varianz eines sicheren Gewinns ist \(0\). Somit erhalten wir für den sicheren Gewinn einen Wert der Präferenzfunktion des risikoaversen Teilnehmers von \[h(75, 0) = 75.00.\] Da für einen risikoaversen Teilnehmer der Wert der Präferenzfunktion des Glücksspiels mit \(90.35\) größer ist als der Wert der Präferenzfunktion eines sicheren Gewinns, entscheidet sich der Teilnehmer für das Glücksspiel und erzielt damit einen Wert der Präferenzfunktion von \(90.35\).

Ein Teilnehmer einer Spielshow im Fernsehen hat die Wahl zwischen zwei Möglichkeiten: Einstreichen eines sicheren Gewinns von \(383\) Euro oder Teilnahme an einem Glücksspiel. Der Gewinn des Glücksspiels wird durch die Zufallsvariable \(G\) beschrieben. Diese hat folgende Wahrscheinlichkeitsfunktion:

\(g\)	\(90\)	\(200\)	\(270\)	\(290\)	\(340\)
\(P(G = g)\)	\(0.15\)	\(0.17\)	\(0.26\)	\(0.36\)	\(0.06\)

Nehmen Sie an, der Teilnehmer hat eine von dem Erwartungswert \(\mu\) und der Standardabweichung \(\sigma\) des Gewinns abhängige Präferenzfunktion \(h(\mu, \sigma)\):
\[h(\mu, \sigma) = \left\{ \begin{array}{ll} \mu + \sigma & \mbox{risikofreudiger Teilnehmer,} \\ \mu & \mbox{risikoneutraler Teilnehmer,} \\ \mu - \sigma & \mbox{risikoaverser Teilnehmer.} \end{array} \right.\]

Nach der Präferenztheorie entscheidet sich der Teilnehmer so zwischen den beiden Möglichkeiten, dass der Wert der Präferenzfunktion maximiert wird. Berechnen Sie den Wert der Präferenzfunktion, den ein risikofreudiger Teilnehmer nach seiner Entscheidung erzielt.

Bei dem Glücksspiel berechnet sich der erwartete Gewinn durch: \[\begin{aligned} E(G) &=& 90 \cdot P(G = 90) + 200 \cdot P(G = 200) + 270 \cdot P(G = 270) + 290 \cdot P(G = 290) + 340 \cdot P(G = 340) \\ &=& 90 \cdot 0.15 + 200 \cdot 0.17 + 270 \cdot 0.26 + 290 \cdot 0.36 + 340 \cdot 0.06 \\ &=& 242.50. \end{aligned}\] Die Standardabweichung des Glücksspiels ergibt sich durch: \[\begin{aligned} E(G^2) &=& 90^2 \cdot P(G = 90) + 200^2 \cdot P(G = 200) + 270^2 \cdot P(G = 270) + 290^2 \cdot P(G = 290) + 340^2 \cdot P(G = 340) \\ &=& 8100 \cdot 0.15 + 40000 \cdot 0.17 + 72900 \cdot 0.26 + 84100 \cdot 0.36 + 115600 \cdot 0.06 \\ &=& 64181 \\ V(G) &=& E(G^2) - (E(G))^2 = 64181 - 242.5^2 = 5374.75 \\ \sigma(G) &=& \sqrt{5374.75} = 73.3127. \end{aligned}\] Damit erhalten wir für das Glücksspiel einen Wert der Präferenzfunktion des risikofreudigen Teilnehmers von \[h(242.50, 73.3127) \approx 315.81.\]

Der erwartete Gewinn der sicheren Auszahlung entspricht genau dem dabei erhaltenen Betrag, also \(383.00\). Die Varianz eines sicheren Gewinns ist \(0\). Somit erhalten wir für den sicheren Gewinn einen Wert der Präferenzfunktion des risikofreudigen Teilnehmers von \[h(383, 0) = 383.00.\] Da für einen risikofreudigen Teilnehmer der Wert der Präferenzfunktion des Glücksspiels mit \(315.81\) kleiner ist als der Wert der Präferenzfunktion eines sicheren Gewinns, entscheidet sich der Teilnehmer für den sicheren Gewinn und erzielt damit einen Wert der Präferenzfunktion von \(383.00\).

Ein Teilnehmer einer Spielshow im Fernsehen hat die Wahl zwischen zwei Möglichkeiten: Einstreichen eines sicheren Gewinns von \(261\) Euro oder Teilnahme an einem Glücksspiel. Der Gewinn des Glücksspiels wird durch die Zufallsvariable \(G\) beschrieben. Diese hat folgende Wahrscheinlichkeitsfunktion:

\(g\)	\(100\)	\(180\)	\(240\)	\(280\)	\(290\)
\(P(G = g)\)	\(0.20\)	\(0.09\)	\(0.21\)	\(0.23\)	\(0.27\)

Nehmen Sie an, der Teilnehmer hat eine von dem Erwartungswert \(\mu\) und der Standardabweichung \(\sigma\) des Gewinns abhängige Präferenzfunktion \(h(\mu, \sigma)\):
\[h(\mu, \sigma) = \left\{ \begin{array}{ll} \mu + \sigma & \mbox{risikofreudiger Teilnehmer,} \\ \mu & \mbox{risikoneutraler Teilnehmer,} \\ \mu - \sigma & \mbox{risikoaverser Teilnehmer.} \end{array} \right.\]

Nach der Präferenztheorie entscheidet sich der Teilnehmer so zwischen den beiden Möglichkeiten, dass der Wert der Präferenzfunktion maximiert wird. Berechnen Sie den Wert der Präferenzfunktion, den ein risikofreudiger Teilnehmer nach seiner Entscheidung erzielt.

Bei dem Glücksspiel berechnet sich der erwartete Gewinn durch: \[\begin{aligned} E(G) &=& 100 \cdot P(G = 100) + 180 \cdot P(G = 180) + 240 \cdot P(G = 240) + 280 \cdot P(G = 280) + 290 \cdot P(G = 290) \\ &=& 100 \cdot 0.20 + 180 \cdot 0.09 + 240 \cdot 0.21 + 280 \cdot 0.23 + 290 \cdot 0.27 \\ &=& 229.30. \end{aligned}\] Die Standardabweichung des Glücksspiels ergibt sich durch: \[\begin{aligned} E(G^2) &=& 100^2 \cdot P(G = 100) + 180^2 \cdot P(G = 180) + 240^2 \cdot P(G = 240) + 280^2 \cdot P(G = 280) + 290^2 \cdot P(G = 290) \\ &=& 10000 \cdot 0.20 + 32400 \cdot 0.09 + 57600 \cdot 0.21 + 78400 \cdot 0.23 + 84100 \cdot 0.27 \\ &=& 57751 \\ V(G) &=& E(G^2) - (E(G))^2 = 57751 - 229.3^2 = 5172.51 \\ \sigma(G) &=& \sqrt{5172.51} = 71.9202. \end{aligned}\] Damit erhalten wir für das Glücksspiel einen Wert der Präferenzfunktion des risikofreudigen Teilnehmers von \[h(229.30, 71.9202) \approx 301.22.\]

Der erwartete Gewinn der sicheren Auszahlung entspricht genau dem dabei erhaltenen Betrag, also \(261.00\). Die Varianz eines sicheren Gewinns ist \(0\). Somit erhalten wir für den sicheren Gewinn einen Wert der Präferenzfunktion des risikofreudigen Teilnehmers von \[h(261, 0) = 261.00.\] Da für einen risikofreudigen Teilnehmer der Wert der Präferenzfunktion des Glücksspiels mit \(301.22\) größer ist als der Wert der Präferenzfunktion eines sicheren Gewinns, entscheidet sich der Teilnehmer für das Glücksspiel und erzielt damit einen Wert der Präferenzfunktion von \(301.22\).

Normalverteilung

a

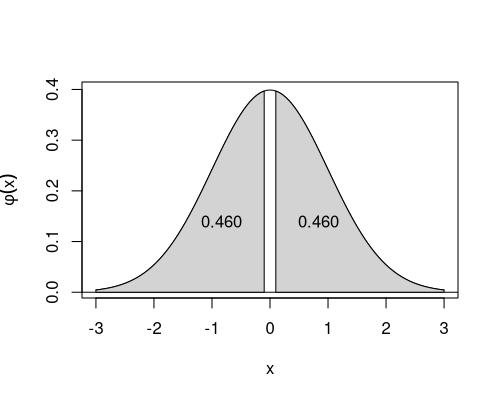
Die Zufallsgröße \(Z\) ist standardnormalverteilt. Berechnen Sie \(P(Z^2 > 0.01)\). (Geben Sie das Ergebnis auf drei Nachkommastellen genau an.)

Umformen und aus der Normalverteilungstabelle ablesen: \[\begin{aligned} P(Z^2 > 0.01) & = & P(|Z| > 0.10) \\ & = & P(Z > 0.10) + P(Z < -0.10) \\ & = & P(Z < -0.10) + P(Z < -0.10) \\ & = & 2 \cdot 0.460 \\ & = & 0.920 \end{aligned}\]

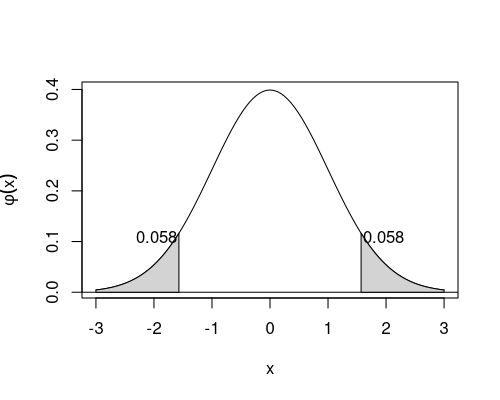
Die Zufallsgröße \(Z\) ist standardnormalverteilt. Berechnen Sie \(P(|Z| > 1.57)\). (Geben Sie das Ergebnis auf drei Nachkommastellen genau an.)

Umformen und aus der Normalverteilungstabelle ablesen: \[\begin{aligned} P(|Z| > 1.57) & = & P(Z > 1.57) + P(Z < -1.57) \\ & = & P(Z < -1.57) + P(Z < -1.57) \\ & = & 2 \cdot 0.058 \\ & = & 0.116 \end{aligned}\]

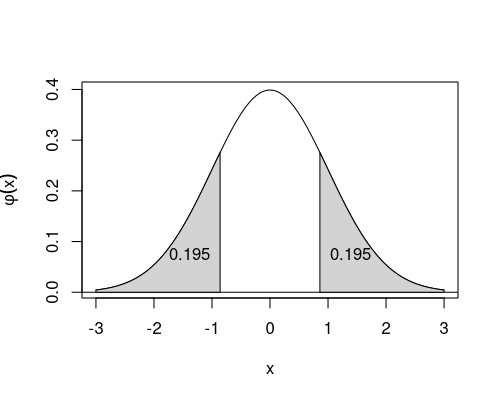
Die Zufallsgröße \(Z\) ist standardnormalverteilt. Berechnen Sie \(P(|Z| > 0.86)\). (Geben Sie das Ergebnis auf drei Nachkommastellen genau an.)

Umformen und aus der Normalverteilungstabelle ablesen: \[\begin{aligned} P(|Z| > 0.86) & = & P(Z > 0.86) + P(Z < -0.86) \\ & = & P(Z < -0.86) + P(Z < -0.86) \\ & = & 2 \cdot 0.195 \\ & = & 0.390 \end{aligned}\]

b

Die Rendite eines Wertpapiers \(X\) folgt einer Normalverteilung mit Mittelwert \(\mu = 0.19\) und Standardabweichung \(\sigma = 0.37\). Wie groß ist die Wahrscheinlichkeit, dass die Rendite nicht größer als \(0.68\) wird? (Geben Sie das Ergebnis in Prozent an.)

Wenn \(X\) normalverteilt mit Mittelwert \(\mu = 0.19\) und Standardabweichung \(\sigma = 0.37\) ist, dann ist

\[\begin{aligned} Z = \frac{X - 0.19}{0.37} \end{aligned}\]

die zugehörige standardisierte Zufallsgröße, d.h. \(Z\) ist standardnormalverteilt.

Die Wahrscheinlichkeit \(P(X \leq 0.68 )\) berechnen wir, indem wir auf beiden Seiten der Ungleichung standardisieren und dann die Wahrscheinlichkeit für die standardisierte normalverteilte Größe ermitteln.

Die exakte Berechnung der Wahrscheinlichkeit ergibt folgendes Ergebnis:

\[\begin{aligned} P(X \leq 0.68) = P \left( \frac{X - 0.19}{0.37} \leq \frac{0.68 - 0.19}{0.37}\right) = P \left(Z \leq 1.324324 \right) = 0.907302. \end{aligned}\]

Wird hingegen die Normalverteilungstabelle zur Lösung der Aufgabe verwendet, dann erhält man:

\[\begin{aligned} P \left(Z \leq 1.32 \right) = 0.907. \end{aligned}\]

Die Wahrscheinlichkeit, dass die Rendite nicht größer als \(0.68\) wird, beträgt somit \(90.73\)% (exakte Berechnung) bzw. \(90.70\)% (Berechnung anhand der Normalverteilungstabelle).

Die Rendite eines Wertpapiers \(X\) ist normalverteilt mit Mittelwert \(\mu = 0.06\) und Varianz \(\sigma^{2} = 0.12\). Wie groß ist die Wahrscheinlichkeit, dass die Rendite nicht größer als \(0.34\) wird? (Geben Sie das Ergebnis in Prozent an.)

Wenn \(X\) normalverteilt mit Mittelwert \(\mu = 0.06\) und Varianz \(\sigma^{2} = 0.12\) ist, dann ist

\[\begin{aligned} Z = \frac{X - 0.06}{\sqrt{ 0.12 }} \end{aligned}\]

die zugehörige standardisierte Zufallsgröße, d.h. \(Z\) ist standardnormalverteilt.

Die Wahrscheinlichkeit \(P(X \leq 0.34 )\) berechnen wir, indem wir auf beiden Seiten der Ungleichung standardisieren und dann die Wahrscheinlichkeit für die standardisierte normalverteilte Größe ermitteln.

Die exakte Berechnung der Wahrscheinlichkeit ergibt folgendes Ergebnis:

\[\begin{aligned} P(X \leq 0.34) = P \left( \frac{X - 0.06}{\sqrt{ 0.12 }} \leq \frac{0.34 - 0.06}{\sqrt{ 0.12 }}\right) = P \left(Z \leq 0.80829 \right) = 0.790538. \end{aligned}\]

Wird hingegen die Normalverteilungstabelle zur Lösung der Aufgabe verwendet, dann erhält man:

\[\begin{aligned} P \left(Z \leq 0.81 \right) = 0.791. \end{aligned}\]

Die Wahrscheinlichkeit, dass die Rendite nicht größer als \(0.34\) wird, beträgt somit \(79.05\)% (exakte Berechnung) bzw. \(79.10\)% (Berechnung anhand der Normalverteilungstabelle).

Die Rendite eines Wertpapiers \(X\) sei normalverteilt mit Mittelwert \(\mu = 0.14\) und Varianz \(\sigma^{2} = 0.34\). Wie groß ist die Wahrscheinlichkeit, dass die Rendite größer als \(0.11\) wird? (Geben Sie das Ergebnis in Prozent an.)

Wenn \(X\) normalverteilt mit Mittelwert \(\mu = 0.14\) und Varianz \(\sigma^{2} = 0.34\) ist, dann ist

\[\begin{aligned} Z = \frac{X - 0.14}{\sqrt{ 0.34 }} \end{aligned}\]

die zugehörige standardisierte Zufallsgröße, d.h. \(Z\) ist standardnormalverteilt.

Die Wahrscheinlichkeit \(P(X > 0.11 ) = 1 - P(X \leq 0.11 )\) berechnen wir, indem wir auf beiden Seiten der Ungleichung standardisieren und dann die Wahrscheinlichkeit für die standardisierte normalverteilte Größe ermitteln.

Die exakte Berechnung der Wahrscheinlichkeit ergibt folgendes Ergebnis:

\[\begin{aligned} P(X > 0.11) = 1- P \left( \frac{X - 0.14}{\sqrt{ 0.34 }} \leq \frac{0.11 - 0.14}{\sqrt{ 0.34 }}\right) = 1- P \left(Z \leq -0.05145 \right) = 0.520516. \end{aligned}\]

Wird hingegen die Normalverteilungstabelle zur Lösung der Aufgabe verwendet, dann erhält man:

\[\begin{aligned} 1- P \left(Z \leq -0.05 \right) = 0.52. \end{aligned}\]

Die Wahrscheinlichkeit, dass die Rendite größer als \(0.11\) wird, beträgt somit \(52.05\)% (exakte Berechnung) bzw. \(52.00\)% (Berechnung anhand der Normalverteilungstabelle).

c

Der Benzinverbrauch eines PKW-Modells (in Liter pro \(100\) km) sei normalverteilt mit Mittelwert \(\mu = 12.47\) und Varianz \(\sigma^{2} = 26.32\). Welcher Verbrauch wird von \(78\) Prozent der PKW überschritten?

(Geben Sie das Ergebnis auf zwei Nachkommastellen genau an.)

Wenn der Benzinverbrauch \(X\) normalverteilt mit Mittelwert \(\mu = 12.47\) und Varianz \(\sigma^{2} = 26.32\) ist, dann ist \[Z = \frac{X - 12.47}{\sqrt{ 26.32 }}\] die zugehörige standardisierte Zufallsgröße, d.h. \(Z\) ist standardnormalverteilt.

\[0.78 = P(X > x) = P\left(\frac{X- 12.47}{\sqrt{ 26.32 }} > \frac{x - 12.47}{\sqrt{ 26.32 }}\right) = P\left(Z > \frac{x - 12.47}{\sqrt{ 26.32 }}\right)\] Das ist gleichbedeutend mit
\[P\left( Z \leq \frac{x - 12.47}{\sqrt{ 26.32 }} \right) = 0.22\] Die Größe auf der rechten Seite der Ungleichung muss also das \(0.22\)-Quantil \(N_{0.22}\) von der standardnormalverteilten Größe \(Z\) sein.
Die exakte Berechnung des Quantils ergibt folgendes Ergebnis: \[\begin{aligned} \frac{x - 12.47}{\sqrt{ 26.32 }} & = & -0.772193 \\ x & = & 12.47 -0.772193 \cdot \sqrt{ 26.32 } \\ & = & 8.508416 \approx 8.51 \end{aligned}\] Wird hingegen die Tabelle Quantile der Standardnormalverteilung zur Lösung der Aufgabe verwendet, dann erhält man: \[\begin{aligned} \frac{x - 12.47}{\sqrt{ 26.32 }} & = & -0.7722 \\ x & = & 12.47 -0.7722 \cdot \sqrt{ 26.32 } \\ & = & 8.5084 \approx 8.51 \end{aligned}\] Das \(0.22\)-Quantil von \(X\) beträgt somit \(8.51\) (exakte Berechnung) bzw. \(8.51\) (Berechnung anhand der Tabelle Quantile der Standardnormalverteilung).

Der Benzinverbrauch eines PKW-Modells (in Liter pro \(100\) km) ist normalverteilt mit Mittelwert \(\mu = 10.51\) und Standardabweichung \(\sigma = 3.86\). Welcher Verbrauch wird von \(55\) Prozent der PKW nicht überschritten?

(Geben Sie das Ergebnis auf zwei Nachkommastellen genau an.)

Wenn der Benzinverbrauch \(X\) normalverteilt mit Mittelwert \(\mu = 10.51\) und Standardabweichung \(\sigma = 3.86\) ist, dann ist \[Z = \frac{X - 10.51}{3.86}\] die zugehörige standardisierte Zufallsgröße, d.h. \(Z\) ist standardnormalverteilt.

\[0.55 = P(X \leq x) = P\left(\frac{X- 10.51}{3.86} \leq \frac{x - 10.51}{3.86}\right) = P\left(Z \leq \frac{x - 10.51}{3.86}\right)\] \[P \left( Z \leq \frac{x - 10.51}{3.86}\right) = 0.55\] Die Größe auf der rechten Seite der Ungleichung muss also das \(0.55\)-Quantil \(N_{0.55}\) von der standardnormalverteilten Größe \(Z\) sein.
Die exakte Berechnung des Quantils ergibt folgendes Ergebnis: \[\begin{aligned} \frac{x - 10.51}{3.86} & = & 0.125661 \\ x & = & 10.51 + 0.125661 \cdot 3.86 \\ & = & 10.995053 \approx 11.00 \end{aligned}\] Wird hingegen die Tabelle Quantile der Standardnormalverteilung zur Lösung der Aufgabe verwendet, dann erhält man: \[\begin{aligned} \frac{x - 10.51}{3.86} & = & 0.1257 \\ x & = & 10.51 + 0.1257 \cdot 3.86 \\ & = & 10.9952 \approx 11.00 \end{aligned}\] Das \(0.55\)-Quantil von \(X\) beträgt somit \(11.00\) (exakte Berechnung) bzw. \(11.00\) (Berechnung anhand der Tabelle Quantile der Standardnormalverteilung).

Der Benzinverbrauch eines PKW-Modells (in Liter pro \(100\) km) ist normalverteilt mit Mittelwert \(\mu = 5.13\) und Varianz \(\sigma^{2} = 0.62\). Welcher Verbrauch wird von \(82\) Prozent der PKW überschritten?

(Geben Sie das Ergebnis auf zwei Nachkommastellen genau an.)

Wenn der Benzinverbrauch \(X\) normalverteilt mit Mittelwert \(\mu = 5.13\) und Varianz \(\sigma^{2} = 0.62\) ist, dann ist \[Z = \frac{X - 5.13}{\sqrt{ 0.62 }}\] die zugehörige standardisierte Zufallsgröße, d.h. \(Z\) ist standardnormalverteilt.

\[0.82 = P(X > x) = P\left(\frac{X- 5.13}{\sqrt{ 0.62 }} > \frac{x - 5.13}{\sqrt{ 0.62 }}\right) = P\left(Z > \frac{x - 5.13}{\sqrt{ 0.62 }}\right)\] Das ist gleichbedeutend mit
\[P\left( Z \leq \frac{x - 5.13}{\sqrt{ 0.62 }} \right) = 0.18\] Die Größe auf der rechten Seite der Ungleichung muss also das \(0.18\)-Quantil \(N_{0.18}\) von der standardnormalverteilten Größe \(Z\) sein.
Die exakte Berechnung des Quantils ergibt folgendes Ergebnis: \[\begin{aligned} \frac{x - 5.13}{\sqrt{ 0.62 }} & = & -0.915365 \\ x & = & 5.13 -0.915365 \cdot \sqrt{ 0.62 } \\ & = & 4.409241 \approx 4.41 \end{aligned}\] Wird hingegen die Tabelle Quantile der Standardnormalverteilung zur Lösung der Aufgabe verwendet, dann erhält man: \[\begin{aligned} \frac{x - 5.13}{\sqrt{ 0.62 }} & = & -0.9154 \\ x & = & 5.13 -0.9154 \cdot \sqrt{ 0.62 } \\ & = & 4.4092 \approx 4.41 \end{aligned}\] Das \(0.18\)-Quantil von \(X\) beträgt somit \(4.41\) (exakte Berechnung) bzw. \(4.41\) (Berechnung anhand der Tabelle Quantile der Standardnormalverteilung).

d

Die Zufallsgröße \(Z\) ist standardnormalverteilt. Berechnen Sie \({P(9 Z+ 8 > 5)}\).

(Geben Sie das Ergebnis auf drei Nachkommastellen genau an.)

Umformen und aus der Normalverteilungstabelle ablesen: \[\begin{aligned} P(9 Z + 8 > 5) & = & P \left( Z > \frac{5 - 8}{9} \right) \\ & = & P \left( Z > -0.333333 \right) \\ & = & 1 - P \left( Z \le -0.33 \right) \\ & = & 0.629 \end{aligned}\]

Die Zufallsgröße \(Z\) ist standardnormalverteilt. Berechnen Sie \({P(20 Z+ 11 > 6)}\).

(Geben Sie das Ergebnis auf drei Nachkommastellen genau an.)

Umformen und aus der Normalverteilungstabelle ablesen: \[\begin{aligned} P(20 Z + 11 > 6) & = & P \left( Z > \frac{6 - 11}{20} \right) \\ & = & P \left( Z > -0.25 \right) \\ & = & 1 - P \left( Z \le -0.25 \right) \\ & = & 0.599 \end{aligned}\]

Die Zufallsgröße \(Z\) ist standardnormalverteilt. Berechnen Sie \({P(16 Z+ 3 \le 6)}\).

(Geben Sie das Ergebnis auf drei Nachkommastellen genau an.)

Umformen und aus der Normalverteilungstabelle ablesen: \[\begin{aligned} P(16 Z + 3 \le 6) & = & P \left( Z \le \frac{6 - 3}{16} \right) \\ & = & P \left( Z \le 0.1875 \right) \\ & = & P \left( Z \le 0.19 \right) \\ & = & 0.575 \end{aligned}\]

e

Die jährliche Nachfrage nach einem Produkt ist eine normalverteilte zufällige Größe mit Erwartungswert \(280\) und Standardabweichung \(49\).

Wie viele Mengeneinheiten müssten produziert werden, damit die Wahrscheinlichkeit dafür, dass die Nachfrage die produzierte Menge unterschreitet, höchstens \(1\) Prozent beträgt?

Es sei \(X\) die jährliche Nachfrage und \(x\) die produzierte Menge.
Wir suchen \(x\) so, dass \[\begin{aligned} 0.01 = P(X < x) & = & P\left(\frac{X - 280}{49} < \frac{x - 280}{49}\right) = P\left(Z < \frac{x - 280}{49}\right) \end{aligned}\] Die Größe auf der rechten Seite der Ungleichung muss also das \(0.01\)-Quantil \(N_{0.01}\) von der standardnormalverteilten Zufallsgröße \(Z\) sein.
Die exakte Berechnung des Quantils ergibt folgendes Ergebnis: \[\begin{aligned} \frac{x - 280}{49} & = & N_{0.01} = -2.326348\\ \frac{x - 280}{49} & = & -2.326348\\ x & = & 280 -2.326348 \cdot 49\\ x & = & 166.008954 \approx 166.01 \end{aligned}\] Wird hingegen die Tabelle Quantile der Standardnormalverteilung zur Lösung der Aufgabe verwendet, dann erhält man: \[\begin{aligned} \frac{x - 280}{49} & = & N_{0.01} = -2.3263\\ \frac{x - 280}{49} & = & -2.3263\\ x & = & 280 -2.3263 \cdot 49\\ x & = & 166.0113 \approx 166.01 \end{aligned}\] Es müssen mindestens \(166.01\) Mengeneinheiten (exakte Berechnung) bzw. \(166.01\) Mengeneinheiten (Berechnung anhand der Tabelle Quantile der Standardnormalverteilung) produziert werden.

Die jährliche Nachfrage nach einem Produkt ist eine normalverteilte zufällige Größe mit Erwartungswert \(170\) und Varianz \(2401\).

Wie viele Mengeneinheiten müssten produziert werden, damit die Wahrscheinlichkeit dafür, dass die Nachfrage die produzierte Menge unterschreitet, höchstens \(7\) Prozent beträgt?

Es sei \(X\) die jährliche Nachfrage und \(x\) die produzierte Menge.
Wir suchen \(x\) so, dass \[\begin{aligned} 0.07 = P(X < x) & = & P\left(\frac{X - 170}{\sqrt{ 2401 }} < \frac{x - 170}{\sqrt{ 2401 }}\right) = P\left(Z < \frac{x - 170}{\sqrt{ 2401 }}\right) \end{aligned}\] Die Größe auf der rechten Seite der Ungleichung muss also das \(0.07\)-Quantil \(N_{0.07}\) von der standardnormalverteilten Zufallsgröße \(Z\) sein.
Die exakte Berechnung des Quantils ergibt folgendes Ergebnis: \[\begin{aligned} \frac{x - 170}{\sqrt{ 2401 }} & = & N_{0.07} = -1.475791\\ \frac{x - 170}{\sqrt{ 2401 }} & = & -1.475791\\ x & = & 170 -1.475791 \cdot \sqrt{ 2401 }\\ x & = & 97.68624 \approx 97.69 \end{aligned}\] Wird hingegen die Tabelle Quantile der Standardnormalverteilung zur Lösung der Aufgabe verwendet, dann erhält man: \[\begin{aligned} \frac{x - 170}{\sqrt{ 2401 }} & = & N_{0.07} = -1.4758\\ \frac{x - 170}{\sqrt{ 2401 }} & = & -1.4758\\ x & = & 170 -1.4758 \cdot \sqrt{ 2401 }\\ x & = & 97.6858 \approx 97.69 \end{aligned}\] Es müssen mindestens \(97.69\) Mengeneinheiten (exakte Berechnung) bzw. \(97.69\) Mengeneinheiten (Berechnung anhand der Tabelle Quantile der Standardnormalverteilung) produziert werden.

Die jährliche Nachfrage nach einem Produkt ist eine normalverteilte zufällige Größe mit Erwartungswert \(260\) und Varianz \(1024\).

Wie viele Mengeneinheiten müssten produziert werden, damit die Wahrscheinlichkeit dafür, dass die Nachfrage die produzierte Menge übersteigt, höchstens \(6\) Prozent beträgt?

Es sei \(X\) die jährliche Nachfrage und \(x\) die produzierte Menge.
Wir suchen \(x\) so, dass \[\begin{aligned} 0.06 = P(X > x) & = & 1- P\left(\frac{X - 260}{\sqrt{ 1024 }} < \frac{x - 260}{\sqrt{ 1024 }}\right) = 1- P\left(Z < \frac{x - 260}{\sqrt{ 1024 }}\right) \\ 1 - 0.06& = & P\left(Z \leq \frac{x - 260}{32}\right) = 0.94 \end{aligned}\] Die Größe auf der rechten Seite der Ungleichung muss also das \(0.94\)-Quantil \(N_{0.94}\) von der standardnormalverteilten Zufallsgröße \(Z\) sein.
Die exakte Berechnung des Quantils ergibt folgendes Ergebnis: \[\begin{aligned} \frac{x - 260}{\sqrt{ 1024 }} & = & N_{0.94} = 1.554774\\ \frac{x - 260}{\sqrt{ 1024 }} & = & 1.554774\\ x & = & 260 + 1.554774 \cdot \sqrt{ 1024 }\\ x & = & 309.752755 \approx 309.75 \end{aligned}\] Wird hingegen die Tabelle Quantile der Standardnormalverteilung zur Lösung der Aufgabe verwendet, dann erhält man: \[\begin{aligned} \frac{x - 260}{\sqrt{ 1024 }} & = & N_{0.94} = 1.5548\\ \frac{x - 260}{\sqrt{ 1024 }} & = & 1.5548\\ x & = & 260 + 1.5548 \cdot \sqrt{ 1024 }\\ x & = & 309.7536 \approx 309.75 \end{aligned}\] Es müssen mindestens \(309.75\) Mengeneinheiten (exakte Berechnung) bzw. \(309.75\) Mengeneinheiten (Berechnung anhand der Tabelle Quantile der Standardnormalverteilung) produziert werden.

f

Der Intelligenzquotient sei normalverteilt mit \(\mu = 100\) und \(\sigma = 15\). Ein Kind gilt als überdurchschnittlich intelligent, wenn es bei einem Test einen IQ von über \(118\) erzielt. Eine Schulklasse mit \(13\) Kindern wird getestet. Wie wahrscheinlich ist es, dass in dieser Klasse mehr als zwei überdurchschnittlich intelligente Kinder zu finden sind?

Zunächst wird die Wahrscheinlichkeit dafür berechnet, dass ein Kind einen \(IQ > 118\) aufweist.
\[\begin{aligned} P( IQ > 118) &=& 1 - P (IQ \leq 118)\\ &=& 1 - \Phi\left(\frac{118 - 100}{15}\right) \\ &=& 1 - \Phi(1.2) \\ &=& 0.115. \end{aligned}\]

Die Anzahl \(X\) der überdurchschnittlich Intelligenten in der Klasse ist binomialverteilt mit \(n = 13\) und \(p = 0.115\) (Unabhängigkeit vorausgesetzt).
\[\begin{aligned} P(X > 2) &=& 1 - P(X \leq 2) = 1 - \left[ P(X = 0) + P(X = 1) + P(X = 2)\right]\\ &=& 1 - \left[ \left(\begin{array}{c} 13 \\ 0\end{array}\right) \cdot 0.115^0 \cdot 0.885^{13} + \left(\begin{array}{c} 13 \\ 1\end{array}\right) \cdot 0.115^1 \cdot 0.885^{12} + \left(\begin{array}{c} 13 \ 2\end{array}\right) \cdot 0.115^2 \cdot 0.885^{11}\right]\\ &=& 1 - [ 0.204297 + 0.345112 + 0.269071] = 0.18152.\\ \end{aligned}\] Die Wahrscheinlichkeit, dass in dieser Klasse mehr als zwei überdurchschnittlich intelligente Kinder zu finden sind, beträgt \(18.15\%\).

Der Intelligenzquotient sei normalverteilt mit \(\mu = 100\) und \(\sigma = 15\). Ein Kind gilt als überdurchschnittlich intelligent, wenn es bei einem Test einen IQ von über \(127\) erzielt. Eine Schulklasse mit \(25\) Kindern wird getestet. Wie wahrscheinlich ist es, dass in dieser Klasse mehr als ein überdurchschnittlich intelligentes Kind zu finden ist?

Zunächst wird die Wahrscheinlichkeit dafür berechnet, dass ein Kind einen \(IQ > 127\) aufweist.
\[\begin{aligned} P( IQ > 127) &=& 1 - P (IQ \leq 127)\\ &=& 1 - \Phi\left(\frac{127 - 100}{15}\right) \\ &=& 1 - \Phi(1.8) \\ &=& 0.036. \end{aligned}\]

Die Anzahl \(X\) der überdurchschnittlich Intelligenten in der Klasse ist binomialverteilt mit \(n = 25\) und \(p = 0.036\) (Unabhängigkeit vorausgesetzt).
\[\begin{aligned} P(X > 1) &=& 1 - P(X \leq 1) = 1 - \left[ P(X = 0) + P(X = 1) \right]\\ &=& 1 - \left[ \left(\begin{array}{c} 25 \\ 0\end{array}\right) \cdot 0.036^0 \cdot 0.964^{25} + \left(\begin{array}{c} 25 \\ 1\end{array}\right) \cdot 0.036^1 \cdot 0.964^{24} \right]\\ &=& 1 - [ 0.399876 + 0.373329 ] = 0.226795.\\ \end{aligned}\] Die Wahrscheinlichkeit, dass in dieser Klasse mehr als ein überdurchschnittlich intelligentes Kind zu finden ist, beträgt \(22.68\%\).

Der Intelligenzquotient sei normalverteilt mit \(\mu = 100\) und \(\sigma = 15\). Ein Kind gilt als überdurchschnittlich intelligent, wenn es bei einem Test einen IQ von über \(115\) erzielt. Eine Schulklasse mit \(12\) Kindern wird getestet. Wie wahrscheinlich ist es, dass in dieser Klasse mehr als ein überdurchschnittlich intelligentes Kind zu finden ist?

Zunächst wird die Wahrscheinlichkeit dafür berechnet, dass ein Kind einen \(IQ > 115\) aufweist.
\[\begin{aligned} P( IQ > 115) &=& 1 - P (IQ \leq 115)\\ &=& 1 - \Phi\left(\frac{115 - 100}{15}\right) \\ &=& 1 - \Phi(1) \\ &=& 0.159. \end{aligned}\]

Die Anzahl \(X\) der überdurchschnittlich Intelligenten in der Klasse ist binomialverteilt mit \(n = 12\) und \(p = 0.159\) (Unabhängigkeit vorausgesetzt).
\[\begin{aligned} P(X > 1) &=& 1 - P(X \leq 1) = 1 - \left[ P(X = 0) + P(X = 1) \right]\\ &=& 1 - \left[ \left(\begin{array}{c} 12 \\ 0\end{array}\right) \cdot 0.159^0 \cdot 0.841^{12} + \left(\begin{array}{c} 12 \\ 1\end{array}\right) \cdot 0.159^1 \cdot 0.841^{11} \right]\\ &=& 1 - [ 0.125185 + 0.28401 ] = 0.590805.\\ \end{aligned}\] Die Wahrscheinlichkeit, dass in dieser Klasse mehr als ein überdurchschnittlich intelligentes Kind zu finden ist, beträgt \(59.08\%\).

Binomialverteilung

a

Die Wahrscheinlichkeit eines schweren Unfalls betrage bei einem technischen Verfahren \({1:2800}\) im Laufe eines Jahres. Wie groß ist die Wahrscheinlichkeit dafür, dass beim Betrieb von \(40\) Anlagen im Laufe von \(15\) Jahren der Unfall genau keinmal auftritt? (Geben Sie das Ergebnis in Prozent an.)

Das Ereignis \(A\) = Auftreten eines schweren Unfalls hat die Wahrscheinlichkeit \[\begin{aligned} P(A) = \frac{1}{2800} = 0.00035714. \end{aligned}\] Das Gegenereignis \(\overline{A}\) = kein Auftreten eines schweren Unfalls hat somit die Wahrscheinlichkeit \[\begin{aligned} P(\overline{A}) = 1 - P(A) = 1 - \frac{1}{2800} = 0.99964286. \end{aligned}\]

Die Zufallsvariable \(X\) = Anzahl schwerer Unfälle ist dann binomialverteilt mit Wahrscheinlichkeit \(P(A) = 1/2800\) und \(n = 40 \cdot 15 = 600\) Versuchen, d.h., \(X \sim B(600, 1/2800)\).

In diesem Fall ist die Wahrscheinlichkeit gesucht, dass genau kein Unfall auftritt. Dies ist die Wahrscheinlichkeit \(P(X = 0)\) .
Es gilt: \[\begin{aligned} P(X = 0) = {600 \choose 0} \cdot 0.000357^{0} \cdot 0.999643^{600} = 0.807087 \end{aligned}\]

Die Wahrscheinlichkeit, dass der Unfall im Laufe von \(15\) Jahren genau keinmal auftritt liegt bei \(80.71\)%.

Die Wahrscheinlichkeit eines schweren Unfalls betrage bei einem technischen Verfahren \({1:3000}\) im Laufe eines Jahres. Wie groß ist die Wahrscheinlichkeit dafür, dass beim Betrieb von \(37\) Anlagen im Laufe von \(8\) Jahren der Unfall genau keinmal auftritt? (Geben Sie das Ergebnis in Prozent an.)

Das Ereignis \(A\) = Auftreten eines schweren Unfalls hat die Wahrscheinlichkeit \[\begin{aligned} P(A) = \frac{1}{3000} = 0.00033333. \end{aligned}\] Das Gegenereignis \(\overline{A}\) = kein Auftreten eines schweren Unfalls hat somit die Wahrscheinlichkeit \[\begin{aligned} P(\overline{A}) = 1 - P(A) = 1 - \frac{1}{3000} = 0.99966667. \end{aligned}\]

Die Zufallsvariable \(X\) = Anzahl schwerer Unfälle ist dann binomialverteilt mit Wahrscheinlichkeit \(P(A) = 1/3000\) und \(n = 37 \cdot 8 = 296\) Versuchen, d.h., \(X \sim B(296, 1/3000)\).

In diesem Fall ist die Wahrscheinlichkeit gesucht, dass genau kein Unfall auftritt. Dies ist die Wahrscheinlichkeit \(P(X = 0)\) .
Es gilt: \[\begin{aligned} P(X = 0) = {296 \choose 0} \cdot 0.000333^{0} \cdot 0.999667^{296} = 0.90603 \end{aligned}\]

Die Wahrscheinlichkeit, dass der Unfall im Laufe von \(8\) Jahren genau keinmal auftritt liegt bei \(90.60\)%.

Die Wahrscheinlichkeit eines schweren Unfalls betrage bei einem technischen Verfahren \({1:3000}\) im Laufe eines Jahres. Wie groß ist die Wahrscheinlichkeit dafür, dass beim Betrieb von \(32\) Anlagen im Laufe von \(7\) Jahren der Unfall genau keinmal auftritt? (Geben Sie das Ergebnis in Prozent an.)

Das Ereignis \(A\) = Auftreten eines schweren Unfalls hat die Wahrscheinlichkeit \[\begin{aligned} P(A) = \frac{1}{3000} = 0.00033333. \end{aligned}\] Das Gegenereignis \(\overline{A}\) = kein Auftreten eines schweren Unfalls hat somit die Wahrscheinlichkeit \[\begin{aligned} P(\overline{A}) = 1 - P(A) = 1 - \frac{1}{3000} = 0.99966667. \end{aligned}\]

Die Zufallsvariable \(X\) = Anzahl schwerer Unfälle ist dann binomialverteilt mit Wahrscheinlichkeit \(P(A) = 1/3000\) und \(n = 32 \cdot 7 = 224\) Versuchen, d.h., \(X \sim B(224, 1/3000)\).

In diesem Fall ist die Wahrscheinlichkeit gesucht, dass genau kein Unfall auftritt. Dies ist die Wahrscheinlichkeit \(P(X = 0)\) .
Es gilt: \[\begin{aligned} P(X = 0) = {224 \choose 0} \cdot 0.000333^{0} \cdot 0.999667^{224} = 0.928041 \end{aligned}\]

Die Wahrscheinlichkeit, dass der Unfall im Laufe von \(7\) Jahren genau keinmal auftritt liegt bei \(92.80\)%.

b

Eine Serienproduktion von Glühbirnen hat einen Ausschussanteil von \(8\%\). Aus der laufenden Produktion wird eine Stichprobe vom Umfang \(31\) entnommen.

Mit welcher Wahrscheinlichkeit enthält diese Stichprobe \(2\) oder mehr defekte Glühbirnen? (Geben Sie das Ergebnis in Prozent an.)

Das Ereignis \(A =\) gefertigte Glühbirne ist defekt hat die Wahrscheinlichkeit \[\begin{aligned} P(A) = 0.08. \end{aligned}\] Das Gegenereignis \(\overline{A} =\) gefertigte Glühbirne funktioniert hat somit die Wahrscheinlichkeit \[\begin{aligned} P(\overline{A}) = 1 - P(A) = 1 - 0.08 = 0.92. \end{aligned}\]

Die Zufallsvariable \(X =\) Anzahl defekter Glübirnen ist dann binomialverteilt mit Wahrscheinlichkeit \(P(A) = 0.08\) und \(n = 31\) Versuchen, d.h., \(X \sim B(31, 0.08)\).

In diesem Fall ist die Wahrscheinlichkeit gesucht, dass \(2\) oder mehr Glübirnen defekt sind. Dies ist die Wahrscheinlichkeit \(P(X \geq 2)\) \[\begin{aligned} P(X \geq 2) &=& 1 - P(X \leq 1) = 1 - \sum_{k = 0}^{1} P(X = k) \\ &=& 1 - \left({31 \choose 0} 0.08^0 (1 - 0.08)^{31 - 0} + \ldots + {31 \choose 1} 0.08^{{1}} (1 - 0.08)^{31 - 1}\right) \\ &=& 1 - 0.27868509 \\ &\approx& 0.7213. \end{aligned}\] Die Wahrscheinlichkeit, dass eine Stichprobe von \(31\) Glühbirnen \(2\) oder mehr Stück Ausschuss enthält, beträgt \(72.13\%\).

Eine Serienproduktion von Glühbirnen hat einen Ausschussanteil von \(9\%\). Aus der laufenden Produktion wird eine Stichprobe vom Umfang \(29\) entnommen.

Mit welcher Wahrscheinlichkeit enthält diese Stichprobe \(2\) oder mehr defekte Glühbirnen? (Geben Sie das Ergebnis in Prozent an.)

Das Ereignis \(A =\) gefertigte Glühbirne ist defekt hat die Wahrscheinlichkeit \[\begin{aligned} P(A) = 0.09. \end{aligned}\] Das Gegenereignis \(\overline{A} =\) gefertigte Glühbirne funktioniert hat somit die Wahrscheinlichkeit \[\begin{aligned} P(\overline{A}) = 1 - P(A) = 1 - 0.09 = 0.91. \end{aligned}\]

Die Zufallsvariable \(X =\) Anzahl defekter Glübirnen ist dann binomialverteilt mit Wahrscheinlichkeit \(P(A) = 0.09\) und \(n = 29\) Versuchen, d.h., \(X \sim B(29, 0.09)\).

In diesem Fall ist die Wahrscheinlichkeit gesucht, dass \(2\) oder mehr Glübirnen defekt sind. Dies ist die Wahrscheinlichkeit \(P(X \geq 2)\) \[\begin{aligned} P(X \geq 2) &=& 1 - P(X \leq 1) = 1 - \sum_{k = 0}^{1} P(X = k) \\ &=& 1 - \left({29 \choose 0} 0.09^0 (1 - 0.09)^{29 - 0} + \ldots + {29 \choose 1} 0.09^{{1}} (1 - 0.09)^{29 - 1}\right) \\ &=& 1 - 0.25101614 \\ &\approx& 0.749. \end{aligned}\] Die Wahrscheinlichkeit, dass eine Stichprobe von \(29\) Glühbirnen \(2\) oder mehr Stück Ausschuss enthält, beträgt \(74.90\%\).

Eine Serienproduktion von Glühbirnen hat einen Ausschussanteil von \(4\%\). Aus der laufenden Produktion wird eine Stichprobe vom Umfang \(57\) entnommen.

Mit welcher Wahrscheinlichkeit enthält diese Stichprobe \(3\) oder mehr defekte Glühbirnen? (Geben Sie das Ergebnis in Prozent an.)

Das Ereignis \(A =\) gefertigte Glühbirne ist defekt hat die Wahrscheinlichkeit \[\begin{aligned} P(A) = 0.04. \end{aligned}\] Das Gegenereignis \(\overline{A} =\) gefertigte Glühbirne funktioniert hat somit die Wahrscheinlichkeit \[\begin{aligned} P(\overline{A}) = 1 - P(A) = 1 - 0.04 = 0.96. \end{aligned}\]

Die Zufallsvariable \(X =\) Anzahl defekter Glübirnen ist dann binomialverteilt mit Wahrscheinlichkeit \(P(A) = 0.04\) und \(n = 57\) Versuchen, d.h., \(X \sim B(57, 0.04)\).

In diesem Fall ist die Wahrscheinlichkeit gesucht, dass \(3\) oder mehr Glübirnen defekt sind. Dies ist die Wahrscheinlichkeit \(P(X \geq 3)\) \[\begin{aligned} P(X \geq 3) &=& 1 - P(X \leq 2) = 1 - \sum_{k = 0}^{2} P(X = k) \\ &=& 1 - \left({57 \choose 0} 0.04^0 (1 - 0.04)^{57 - 0} + \ldots + {57 \choose 2} 0.04^{{2}} (1 - 0.04)^{57 - 2}\right) \\ &=& 1 - 0.59984779 \\ &\approx& 0.4002. \end{aligned}\] Die Wahrscheinlichkeit, dass eine Stichprobe von \(57\) Glühbirnen \(3\) oder mehr Stück Ausschuss enthält, beträgt \(40.02\%\).

c

Der Vorstand eines Vereins hat \(7\) Mitglieder und muss kurzfristig über einen Antrag abstimmen. Nach ausführlicher Debatte stand fest, dass ein Vorstandsmitglied sicher für den Antrag und zwei Vorstandsmitglieder sicher gegen den Antrag stimmen werden. Alle übrigen Vorstandsmitglieder sind vollkommen indifferent und unentschlossen und entscheiden sich zufällig dafür oder dagegen (\(p = 0.5\)). Es wird angenommen, dass geheim abgestimmt wird und damit Unabhängigkeit gewährleistet ist.

Mit welcher Wahrscheinlichkeit wird der Antrag mit Mehrheit angenommen? (Geben Sie das Ergebnis in Prozent an.)

Die Zufallsvariable \(X =\) Anzahl Stimmen von unentschlossenen Vorstandsmitgliedern ist dann binomialverteilt mit Wahrscheinlichkeit \(P(A) = 0.5\) und \(n = 4\) Versuchen, d.h., \(X \sim B(4, 0.5)\).

Da \(1\) der Vorstandsmitglieder sicher dafür und \(2\) sicher dagegen sind, wird für eine Mehrheit für den Antrag die Stimme von \(3\) unentschlossenen Vorstandsmitgliedern gebraucht. Dies ist die Wahrscheinlichkeit \(P(X \geq 3)\) \[\begin{aligned} P(X \geq 3) &=& 1 - P(X \leq 2) = 1 - \sum_{k = 0}^{2} P(X = k) \\ &=& 1 - \left( {4 \choose 0} 0.5^0 (1 - 0.5)^{4 - 0} + \ldots + {4 \choose 2} 0.5^{{2}} (1 - 0.5)^{4 - 2}\right) \\ &=& 1 - 0.6875 \\ &\approx& 0.3125. \end{aligned}\] Die Wahrscheinlichkeit, dass der Antrag angenommen wird, beträgt \(31.25\%\).

Der Vorstand eines Vereins hat \(5\) Mitglieder und muss kurzfristig über einen Antrag abstimmen. Nach ausführlicher Debatte stand fest, dass ein Vorstandsmitglied sicher für den Antrag und ein Vorstandsmitglied sicher gegen den Antrag stimmen werden. Alle übrigen Vorstandsmitglieder sind vollkommen indifferent und unentschlossen und entscheiden sich zufällig dafür oder dagegen (\(p = 0.5\)). Es wird angenommen, dass geheim abgestimmt wird und damit Unabhängigkeit gewährleistet ist.

Mit welcher Wahrscheinlichkeit wird der Antrag mit Mehrheit angenommen? (Geben Sie das Ergebnis in Prozent an.)

Die Zufallsvariable \(X =\) Anzahl Stimmen von unentschlossenen Vorstandsmitgliedern ist dann binomialverteilt mit Wahrscheinlichkeit \(P(A) = 0.5\) und \(n = 3\) Versuchen, d.h., \(X \sim B(3, 0.5)\).

Da \(1\) der Vorstandsmitglieder sicher dafür und \(1\) sicher dagegen sind, wird für eine Mehrheit für den Antrag die Stimme von \(2\) unentschlossenen Vorstandsmitgliedern gebraucht. Dies ist die Wahrscheinlichkeit \(P(X \geq 2)\) \[\begin{aligned} P(X \geq 2) &=& 1 - P(X \leq 1) = 1 - \sum_{k = 0}^{1} P(X = k) \\ &=& 1 - \left( {3 \choose 0} 0.5^0 (1 - 0.5)^{3 - 0} + {3 \choose 1} 0.5^{{1}} (1 - 0.5)^{3 - 1}\right) \\ &=& 1 - 0.5 \\ &\approx& 0.5. \end{aligned}\] Die Wahrscheinlichkeit, dass der Antrag angenommen wird, beträgt \(50.00\%\).

Der Vorstand eines Vereins hat \(7\) Mitglieder und muss kurzfristig über einen Antrag abstimmen. Nach ausführlicher Debatte stand fest, dass ein Vorstandsmitglied sicher für den Antrag und zwei Vorstandsmitglieder sicher gegen den Antrag stimmen werden. Alle übrigen Vorstandsmitglieder sind vollkommen indifferent und unentschlossen und entscheiden sich zufällig dafür oder dagegen (\(p = 0.5\)). Es wird angenommen, dass geheim abgestimmt wird und damit Unabhängigkeit gewährleistet ist.

Mit welcher Wahrscheinlichkeit wird der Antrag mit Mehrheit angenommen? (Geben Sie das Ergebnis in Prozent an.)

Die Zufallsvariable \(X =\) Anzahl Stimmen von unentschlossenen Vorstandsmitgliedern ist dann binomialverteilt mit Wahrscheinlichkeit \(P(A) = 0.5\) und \(n = 4\) Versuchen, d.h., \(X \sim B(4, 0.5)\).

Da \(1\) der Vorstandsmitglieder sicher dafür und \(2\) sicher dagegen sind, wird für eine Mehrheit für den Antrag die Stimme von \(3\) unentschlossenen Vorstandsmitgliedern gebraucht. Dies ist die Wahrscheinlichkeit \(P(X \geq 3)\) \[\begin{aligned} P(X \geq 3) &=& 1 - P(X \leq 2) = 1 - \sum_{k = 0}^{2} P(X = k) \\ &=& 1 - \left( {4 \choose 0} 0.5^0 (1 - 0.5)^{4 - 0} + \ldots + {4 \choose 2} 0.5^{{2}} (1 - 0.5)^{4 - 2}\right) \\ &=& 1 - 0.6875 \\ &\approx& 0.3125. \end{aligned}\] Die Wahrscheinlichkeit, dass der Antrag angenommen wird, beträgt \(31.25\%\).