Das Hauptanliegen der Differentialrechnung ist es, präzise Aussagen über das Änderungsverhalten einer Funktion zu machen. Aber schon seit der Zeit der Entdeckung der Differentialrechnung im 17. Jahrhundert wurde dieses Problem im Zusammenhang mit der Frage gesehen: Wie kann man aus dem bekannten Änderungsverhalten einer Funktion diese selbst rekonstruieren?
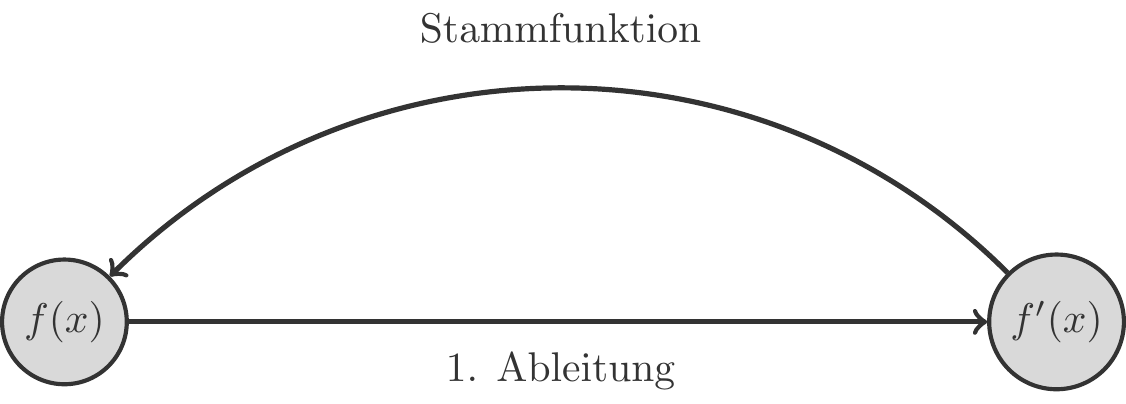
Diese Fragestellung führt uns auf eine erste Deutung des Integralbegriffs: wenn wir die erste Ableitung \(f'(x)\) einer Funktion \(f(x)\) kennen, wie können wir daraus \(f(x)\) bestimmen? Es geht also zunächst darum, den Prozess des Differenzierens umzukehren. Man nennt daher auch \(f(x)\) das Antidifferential oder besser die Stammfunktion von \(f'(x)\). Schematisch können wir uns die Situation so veranschaulichen:
Abbildung 4.1: Formales Differenzieren und Integrieren.
Nun ist, wie wir gesehen haben, der Prozess des Differenzierens ein sehr einfacher, es ist bloß eine handvoll Regeln, die wir in fast mechanischer Weise anwenden können. Daher erwarten wir, dass die Umkehrung dieses Prozesses, das Aufsuchen der Stammfunktion, genauso einfach ist. Aber leider ist das etwas komplizierter. Wie auch immer, wir werden in diesem Kapitel Methoden kennenlernen, die uns mit etwas Routine und Geschick in vielen Fällen (wenn auch lange nicht in allen) die Stammfunktion einer gegebenen Funktion liefern.
In diesem Kapitel werden wir dem Begriff des Integrals aber noch eine zweite Deutung geben, nämlich als Lösung eines Quadraturproblems. Darunter verstehen wir die Berechnung der Fläche zwischen dem Graphen einer Funktion \(f(x)\) und der \(x\)-Achse. Man spricht auch vom bestimmten Integral. Damit stellt sich ganz natürlich die Frage: wie hängen diese beiden Deutungen des Integralbegriffs, das Antidifferential und die Lösung eines Quadraturproblems, zusammen?
Dieser Zusammenhang wird durch den Fundamentalsatz der Analysis hergestellt, einem Kronjuwel der Mathematik, das wir Isaac Newton und Gottfried Leibniz verdanken.
4.1.2 Stammfunktionen
Definition 4.1 Es sei \(F(x)\) eine differenzierbare Funktion und es sei \(f(x)=F'(x)\) ihre Ableitung. Dann nennt man \(F(x)\) eine Stammfunktion von \(f(x)\).
Beispiel 4.2
Offenbar ist \(F(x)=x^2\) eine Stammfunktion von \(f(x)=2x\). Aber auch \(G(x)=x^2+3\) ist eine Stammfunktion von \(f(x)=2x\).
Stammfunktionen sind offensichtlich nicht eindeutig bestimmt. Zu jeder Funktion \(f(x)\), die eine Stammfunktion \(F(x)\) besitzt, gibt es unendlich viele weitere Stammfunktionen. Aber diese Stammfunktionen unterscheiden sich nicht sehr stark.
Satz 4.3 Sind \(F(x)\) und \(G(x)\) zwei Stammfunktionen ein- und derselben Funktion \(f(x)\), dann unterscheiden sich \(F\) und \(G\) nur um eine additive Konstante, dh. \(F(x)=G(x)+C\).
Begründung: Aus \(F'(x)=G'(x)\) folgt, dass \(F'(x)-G'(x)=0\). Nun steht auf der linken Seite dieser Gleichung die Ableitung der Differenz \(F(x)-G(x)\), auf der rechten Seite Null, also die Ableitung einer Konstanten. Daher muss \(F(x)-G(x)\) konstant sein. □
4.1.3 Bestimmte Integrale
Stammfunktionen stehen in enger Beziehung zu bestimmten Integralen. Wir erklären den Begriff des bestimmten Integrals anhand eines Beispiels aus der Finanzmathematik.
Beispiel 4.4 (Kontinuierliche Zahlungsströme)
Es sei \(K(t)\) die Höhe eines Kapitals, das sich im Zeitintervall \([0,T]\) verändert. Wir bezeichnen die Ableitung, also die Änderungsrate des Kapitals \(K(t)\) mit \(k(t)=K'(t)\). Die Kapitalhöhe ist also eine Stammfunktion der Änderungsrate des Kapitals.
In Abschnitt 3.3.3 haben wir das grundlegende Konzept der lokalen Linearisierung von Funktionen behandelt. Dieses erweist sich nun erneut als sehr hilfreich. Angenommen \([t_1,t_2]\) wäre ein Intervall. Dann gilt näherungsweise die Beziehung \[
\begin{gathered}
K(t_2)\approx K(t_1)+k(t_1)(t_2-t_1).
\end{gathered}
\] Diese Gleichung kann so gelesen werden: Auf einem sehr kleinen Zeitintervall \([t_1,t_2]\) kann man die Änderungsrate als annähernd konstant gleich \(k(t_1)\) ansehen. Wenn eine solche konstante Änderungsrate \(k(t_1)\) das Zeitintervall \([t_1,t_2]\) lang wirkt, dann ändert sich das Kapital um \(k(t_1)(t_2-t_1)\).
Wie kann man nun umgekehrt aus der gegebenen Änderungsrate \(k(t)\) den Kapitalverlauf \(K(t)\) rekonstruieren? Diesen Vorgang nennt man Integrieren.
Um den Vorgang des Integrierens besser zu verstehen, stellen wir uns vor, dass das Zeitintervall \([0,T]\) aufgeteilt ist in Teilintervalle \[
\begin{gathered}
0=t_0<t_1<t_2<\ldots<t_{n-1}<t_n=T.
\end{gathered}
\] Dann ist es klar, dass \[
\begin{aligned}
K(T)-K(0)=\;&[K(t_1)-K(t_0)]+[K(t_2)-K(t_1)] +\cdots+ \\
&[K(t_n)-K(t_{n-1})].
\end{aligned}
\] Für jedes der einzelnen kleinen Teilintervalle \([t_{i-1},t_i]\) nehmen wir an, dass die Änderungsrate beginnend mit dem linken Endpunkt annähernd konstant gleich \(k(t_{i-1})\) ist. Dann erhalten wir nach unserer Näherungsformel \[
\begin{gathered}
K(t_i)\approx K(t_{i-1})+k(t_{i-1})(t_i-t_{i-1}),
\end{gathered}
\] und daher \[
\begin{gathered}
\begin{array}{rcl}
K(T)-K(0) & \approx & k(t_0)(t_1-t_0)+k(t_1)(t_2-t_1) \\
& & +\cdots+ k(t_{n-1})(t_n-t_{n-1})\\[2pt]
& = & \displaystyle \sum_{i=1}^n k(t_{i-1})(t_i-t_{i-1}).
\end{array}
\end{gathered}
\tag{4.1}\] Das ist natürlich nur eine Näherungsformel. Die Bedeutung von (4.1) ist in Abbildung 4.2 graphisch dargestellt. Wir sehen daran, dass (4.1) dem Inhalt der grauen Rechteckstreifen entspricht und mit wachsendem \(n\) offenbar immer genauer wird. Um also aus (4.1) eine exakte Gleichung zu machen, müssen wir die Länge der Teilintervalle gegen Null konvergieren lassen, was gleichzeitig heißt, dass die Anzahl der Teilintervalle gegen unendlich strebt.
Abbildung 4.2: Illustration des Grenzübergangs in (4.1).
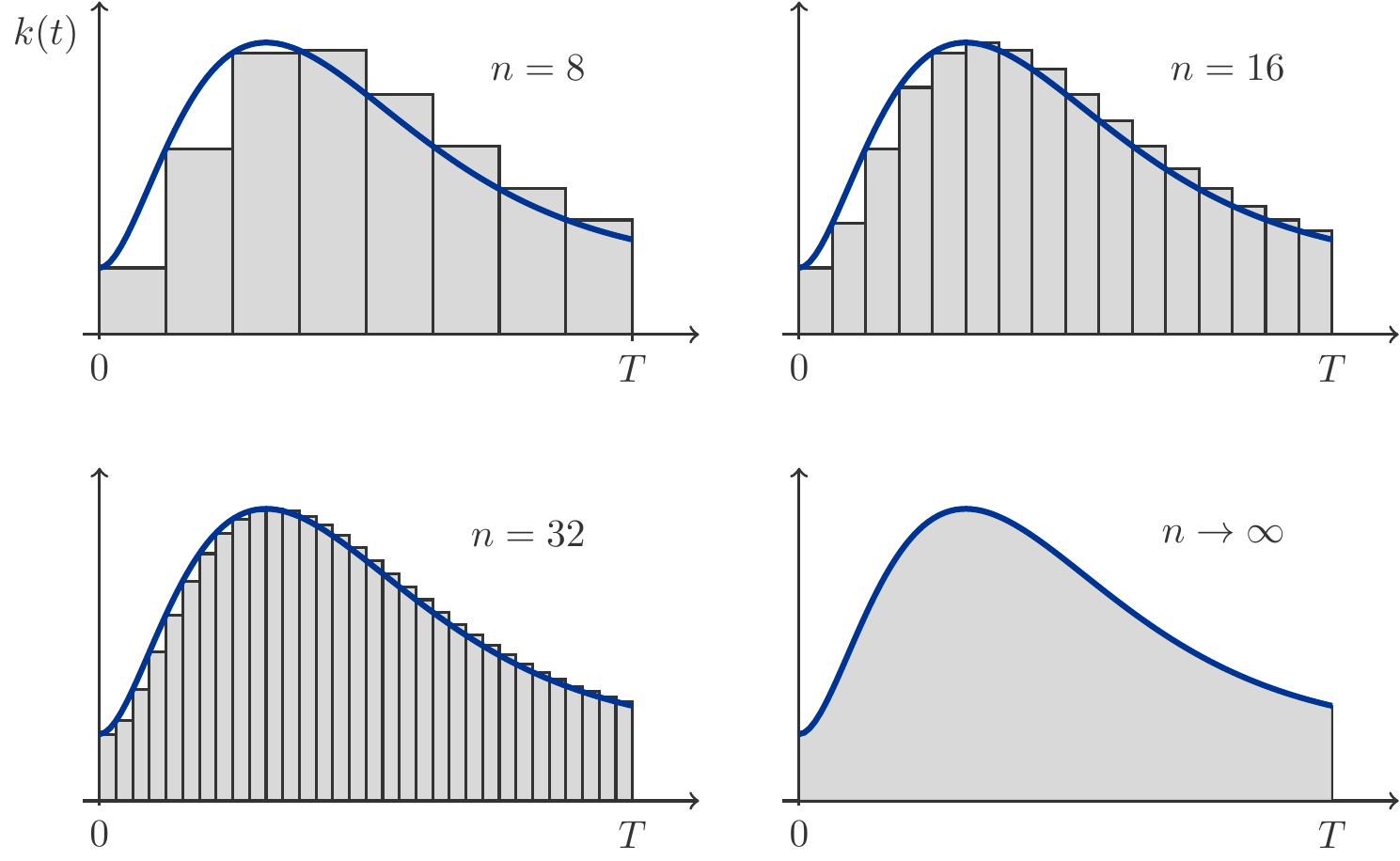
Unter gewissen Voraussetzungen ist es tatsächlich so, dass die Summe auf der rechten Seite zu einem Grenzwert konvergiert. Dieser Grenzwert wird mit dem Symbol \[
\begin{gathered}
\int_0^T k(t)\,\mathrm{d}t
\end{gathered}
\] bezeichnet (das ist eine Stilisierung der Summenschreibweise) und heißt Integral. Dieser Grenzwert entspricht dem Flächeninhalt unterhalb des Graphen der Funktion \(k(t)\) und löst damit ein Quadraturproblem.
Wir erhalten mit dieser Schreibweise die Formel \[
\begin{gathered}
K(T)=K(0)+\int_0^T k(t)\,\,\mathrm{d}t.
\end{gathered}
\tag{4.2}\] Diese Gleichung wird so gelesen: Das Endkapital \(K(T)\) entsteht aus dem Anfangskapital durch Integrieren der Änderungsrate \(k(t)\), dh. durch Aufsummieren der Änderungsrate \(k(t)\), gewichtet mit den Längen \(\mathrm{d}t\) der Teilintervalle, auf denen die Änderungsrate \(k(t)\) wirksam ist.
Wie aber hängen Stammfunktion und Integral zusammen?
Satz 4.5 (Fundamentalsatz der Analysis) Es sei \(f(x)\) eine Funktion, die eine Stammfunktion \(F(x)\) besitzt und es seien \(a,b\in\mathbb R\). Dann gilt \[
\begin{gathered}
\int_a^b f(x)\,\,\mathrm{d}x := F(b)-F(a) = F(x)\Big|_a^b,
\end{gathered}
\tag{4.3}\] und man nennt (4.3) das bestimmte Integral von \(f\) zwischen den Grenzen \(a\) und \(b\).
Eine Konsequenz von (4.1) ist die Additivität des Integrals:
Satz 4.6 (Additivität) Es sei \(a<b<c\), dann gilt: \[
\begin{gathered}
\int_a^cf(x)\,\mathrm{d}x=\int_a^bf(x)\,\mathrm{d}x+\int_b^cf(x)\,\mathrm{d}x.
\end{gathered}
\]
Es spielt keine Rolle, welche spezielle Stammfunktion von \(f(x)\) man für die Definition oder Berechnung eines Integrals verwendet. Da sich verschiedene Stammfunktionen nur durch additive Konstante unterscheiden können, hat die Differenz \(F(b)-F(a)\) für alle Stammfunktionen \(F(x)\) einer Funktion \(f(x)\) den gleichen Wert.
Auch ist es wichtig, sich darüber im klaren zu sei, dass es völlig gleichgültig ist, mit welchem Buchstaben man die Integrationsvariable bezeichnet. Daher sind die folgenden Terme alle gleichwertig: \[
\begin{gathered}
\int_a^b f(x)\,\,\mathrm{d}x=\int_a^b f(y)\,\,\mathrm{d}y=\int_a^b
f(t)\,\,\mathrm{d}t=
\int_a^b f(u)\,\,\mathrm{d}u\,.
\end{gathered}
\] Offensichtlich gilt auch \[
\begin{gathered}
\int_a^b f(x)\,\,\mathrm{d}x =-\int_b^a f(x)\,\,\mathrm{d}x,
\end{gathered}
\] das heißt: Wenn man die Integrationsgrenzen vertauscht, dann ändert sich das Vorzeichen des Integrals.
Angelehnt an das Symbol für das bestimmte Integral verwendet man die Schreibweise \[
\begin{gathered}
\int f(x)\,\,\mathrm{d}x:=F(x)+C
\end{gathered}
\] für die Bezeichnung einer beliebigen Stammfunktion \(F\) von \(f\) und nennt den Ausdruck ein unbestimmtes Integral. Die Zahl \(C\) heißt Integrationskonstante.
4.2 Berechnungsmethoden
Vorweg stellen wir fest, dass es nur für wenige Funktionen mit meist einfachen Funktionstermen möglich ist, Stammfunktionen als geschlossene Terme darzustellen. Wenn dies nicht möglich ist, müssen Stammfunktionen durch Integrale dargestellt werden, die wiederum nur durch Summen näherungsweise berechnet werden können.
Aber manchmal ist es möglich, Stammfunktionen wirklich als Formelterme zu berechnen. Und mit solchen Fällen und Methoden hierzu beschäftigen wir uns in diesem Abschnitt.
Bevor wir in Details gehen formulieren wir eine ganz allgemeine Regel, die eine unmittelbare Folgerung von Definition 4.1 ist:
Jede Ableitungsformel ist zugleich auch eine Formel für eine Stammfunktion. Wir müssen diese Formel nur von rechts nach links lesen.
4.2.1 Grundregeln für das Integrieren
Wir beginnen mit der Ableitungsformel für allgemeine Potenzen (Satz 3.34):
Satz 4.7 (Potenzen) Wenn \(\alpha\not=-1\), dann \[
\begin{gathered}
(x^{\alpha+1})'=(\alpha+1)x^\alpha \quad\implies\quad
\int x^\alpha\,\mathrm{d}x =\frac{x^{\alpha+1}}{\alpha+1}+C.
\end{gathered}
\tag{4.4}\]
Mit dieser Formel können wir für alle beliebigen Potenzen eine Stammfunktion bestimmen, sofern nur der Exponent \(\alpha\ne 1\) ist1. Insbesondere gilt diese Formel auch für \(\alpha=0\): \[
\begin{gathered}
\int x^0\,\mathrm{d}x = \int 1\,\mathrm{d}x = x + C.
\end{gathered}
\tag{4.5}\]
Musteraufgabe 4.8
Man bestimme eine Stammfunktion von \(f(x)=x^5\).
Man berechne \(\displaystyle\int_{-2}^3 x^5 \,\,\mathrm{d}x\).
Lösung: Eine Stammfunktion erhält man durch \[
\begin{gathered}
F(x)=\int x^5\,\,\mathrm{d}x= \frac{x^6}{6}+C.
\end{gathered}
\] Das bestimmte Integral beträgt wegen des Fundamentalsatzes (Satz 4.5): \[
\begin{gathered}
\int_{-2}^3 x^5 \,\,\mathrm{d}x=F(3)-F(-2)=\frac{x^6}{6}\Big|_{-2}^3=
\frac{3^6}{6}-\frac{(-2)^6}{6}=\frac{665}{6}\,.
\end{gathered}
\] □
Musteraufgabe 4.9
Man bestimme eine Stammfunktion von \(g(u)=\frac{1}{\sqrt{u}}\).
Man berechne \(\displaystyle\int_1^{10} \frac{1}{\sqrt{u}}\,\mathrm{d}u\).
Lösung: Wir wenden (4.4) an mit \(\alpha=-1/2\): \[
\begin{gathered}
\int \frac{1}{\sqrt{u}}\,\mathrm{d}u=\int u^{-1/2}\,\mathrm{d}u=
\frac{u^{1/2}}{1/2}=2\sqrt{u}+C.
\end{gathered}
\] Das bestimmte Integral beträgt \[
\begin{gathered}
\int_1^{10} \frac{1}{\sqrt{u}}\,\mathrm{d}u=2\sqrt{u}\Big|_1^{10}=
2\sqrt{10}-2\sqrt{1}=4.325\,.
\end{gathered}
\] □
Die folgende Regel zeigt uns, dass das Aufsuchen der Stammfunktion genauso wie das Differenzieren eine lineare Operation ist.
Satz 4.10 (Summensatz)\[
\begin{gathered}
\int (af(x)+bg(x))\,\mathrm{d}x=a\int f(x)\,\mathrm{d}x+b\int g(x)\,\mathrm{d}x.
\end{gathered}
\] Diese Regel hat zwei Botschaften für uns:
Wir dürfen einen konstanten Faktor vor das Integral ziehen.
Das Integral einer Summe von Funktionen ist die Summe der Integrale.
Musteraufgabe 4.11
Man bestimme eine Stammfunktion von \(\displaystyle
f(x)=3x^2-5+\frac{1}{x^3}\).
Man berechne \(\displaystyle \int_3^7 f(x)\,\,\mathrm{d}x\).
Lösung: Wir wenden den Summensatz (Satz 4.10) an: \[
\begin{aligned}
F(x)&=\int (3x^2-5+\frac{1}{x^{3}})\,\,\mathrm{d}x
=3\int x^2\,\mathrm{d}x-5\int 1\,\mathrm{d}x+\int
x^{-3}\,\mathrm{d}x\\
&=3\frac{x^3}{3}-5x+\frac{x^{-2}}{-2}+C=x^3-5x-\frac{1}{2x^2}+C.
\end{aligned}
\] Das bestimmte Integral hat den Wert: \[
\begin{gathered}
\int_3^7
f(x)\,\mathrm{d}x=\left[x^3-5x-\frac{1}{2x^2}\right]\Bigg|_3^7=296.045\,.
\end{gathered}
\]
Wir erinnern uns: jede Ableitungsformel ist zugleich auch eine Formel für eine Stammfunktion. Damit können wir sofort Stammfunktionen für die Eulersche Exponentialfunktion und den natürlichen Logarithmus angeben.
Satz 4.12 (Exponentialfunktion und Logarithmus) Für Exponentialfunktion und Logarithmus gilt: \[
\begin{gathered}
(e^x)'=e^x \quad\implies\quad \int e^x\,\mathrm{d}x=e^x+C,
\end{gathered}
\] und \[
\begin{gathered}
(\ln(x))'=\frac{1}{x}\quad\implies\quad
\int \frac{1}{x}\,\mathrm{d}x=\ln(x)+C,\quad x>0.
\end{gathered}
\]
Mit diesen Regeln allein kann man aber noch wenig anfangen. Man benötigt zusätzlich jene Integrationsregeln, die sich aus der Produktregel und der Kettenregel für das Differenzieren ergeben.
4.2.2 Partielle Integration
Es sei \(f(x)\) ein Funktionsterm, zu dem man nicht ohne weiteres eine Stammfunktion finden kann. Wir nehmen nun an, dass dieser Funktionsterm das Produkt von zwei Faktoren ist \[
\begin{gathered}
f(x)=g(x)h(x),
\end{gathered}
\] die folgenden Eigenschaften haben:
Zum Faktor \(g(x)\) lässt sich eine Stammfunktion \(G(x)\) direkt angeben.
Der Faktor \(h(x)\) besitzt die Ableitung \(h'(x)\).
Wenn wir auf \(G(x)h(x)\) die Produktregel anwenden: \[
\begin{gathered}
(G(x)h(x))'=g(x)h(x)+G(x)h'(x),
\end{gathered}
\] und zu Stammfunktionen übergehen, dann erhalten wir eine weitere wichtige Regel:
Wir haben damit das ursprüngliche Problem verlagert: Anstatt \(f(x)=g(x)h(x)\) zu integrieren, müssen wir nun die Funktion \(G(x)h'(x)\) integrieren. Wenn wir die Faktoren geschickt gewählt haben, dann ist es möglich, dass das neue Problem einfacher ist als das alte.
Musteraufgabe 4.14
Man bestimme eine Stammfunktion von \(f(x)=x\ln x\).
Man berechne das Integral \(\displaystyle\int_{1}^2 x\ln x\,\mathrm{d}x\).
Lösung: Die Funktion \(f(x)\) ist ein Produkt der Faktoren \(x\) und \(\ln(x)\). Da wir nur von \(x\) auf direktem Weg eine Stammfunktion angeben können (nämlich \(x^2/2\)), wählen wir in (4.6) \(g(x)=x\) und \(h(x)=\ln x\). Mit dieser Wahl: \[
\begin{aligned}
%% {alignat*}{2}
g(x)&=x &\qquad G(x)&=\frac{x^2}{2}\\[4pt]
h(x)&=\ln x & h'(x)&=\frac{1}{x},\end{aligned}
\] finden wir: \[
\begin{aligned}
\int x\ln x\,\mathrm{d}x&=\frac{x^2}{2}\ln x-\int \frac{x^2}{2}
\cdot\frac{1}{x}\,\mathrm{d}x\\[4pt]
&=\frac{x^2}{2}\ln x-\int \frac{x}{2}\,\mathrm{d}x\\
&=\frac{x^2}{2}\ln x-\frac{x^2}{4}+C.
\end{aligned}
\] Das bestimmte Integral beträgt \[
\begin{gathered}
\int_1^2
x\ln x\,\mathrm{d}x=\frac{x^2}{2}\ln x-\frac{x^2}{4}\Bigg|_1^2=2\ln
2-\frac{3}{4}= 0.6363\,.
\end{gathered}
\] □
Musteraufgabe 4.15
Man bestimme eine Stammfunktion von \(f(x)=xe^x\).
Man berechne das Integral \(\displaystyle \int_{-1}^1
xe^x\,\mathrm{d}x\).
Lösung: In diesem Fall kann man bei beiden Faktoren direkt eine Stammfunktion angeben. Es ist dann meist zweckmäßig, jenen Faktor die Rolle von \(h(x)\) übernehmen zu lassen, der sich beim Differenzieren stärker vereinfacht. Im vorliegenden Fall wählen wir daher \(h(x)=x\) und \(g(x)=e^x\). Mit dieser Wahl: \[
\begin{aligned}
g(x)&=e^x &\qquad G(x)&=e^x\\[4pt]
h(x)&=x & h'(x)&=1,\end{aligned}
\] finden wir: \[
\begin{aligned}
\int xe^x\,\mathrm{d}x&=xe^x-\int e^x\,\mathrm{d}x\\
&=xe^x-e^x+C=e^x(x-1)+C.
\end{aligned}
\] Das bestimmte Integral beträgt \[
\begin{gathered}
\int_{-1}^1 xe^x\,\mathrm{d}x = e^x(x-1)\Big|_{-1}^1=2e^{-1}
=0.7358\,.\\
\end{gathered}
\] □
Musteraufgabe 4.16
Man bestimme eine Stammfunktion von \(f(x)=\ln x\).
Man berechne das Integral \(\displaystyle \int_{1}^2
\ln x\,\mathrm{d}x\).
Lösung: Hier ist auf den ersten Blick nicht direkt ersichtlich, dass man dieses Problem mittels partieller Integration lösen kann. Doch auf den zweiten Blick erkennen wir, dass wir ja schreiben können \(\ln x=1\cdot \ln x\) ! Unser Ansatz \[
\begin{aligned}
g(x)&=1 &\qquad G(x)&=x\\[2pt]
h(x)&=\ln x & h'(x)&=\frac{1}{x},
\end{aligned}
\] liefert: \[
\begin{aligned}
\int \ln x\,\mathrm{d}x&=x\ln x-\int x\cdot\frac{1}{x}\,\mathrm{d}x
=x\ln x-\int 1\,\mathrm{d}x\\
&=x\ln x -x+C.
\end{aligned}
\] Mit den angegebenen Integrationsgrenzen: \[
\begin{gathered}
\int_1^2\ln x\,\mathrm{d}x=x\ln x-x\bigg|_1^2=2\ln 2-1=0.3863\,.
\end{gathered}
\] □
4.2.3 Die Substitutionsregel
Unsere Erfahrungen aus Kapitel 3 zeigten uns, dass die Kettenregel die wichtigste Ableitungsregel ist. Da aber jede Ableitungsformel eine Formel für eine Stammfunktion ist, erwarten wir, dass es auch für die Kettenregel so eine Entsprechung geben muss.
Es sei \(H\) eine Stammfunktion von \(h\) und \(g\) sei eine weitere differenzierbare Funktion. Dann sagt die Kettenregel, dass \[
\begin{gathered}
H(g(x))'=h(g(x))g'(x).
\end{gathered}
\] Wenn man diese Gleichung als Aussage über Stammfunktionen umschreibt, dann lautet sie \[
\begin{gathered}
\int h(g(x))g'(x)\,\mathrm{d}x= H(g(x))+C.
\end{gathered}
\tag{4.7}\] Angenommen, wir suchen \(\int h(x)\,\mathrm{d}x\), und eine Stammfunktion \(H(x)\) ist nicht so ohne weiteres (z.B. mittels partieller Integration) zu finden.
Dann können wir eine Substitution versuchen!
Wir setzen \(x=g(t)\), und es wird wegen der Kettenregel: \[
\begin{gathered}
\int h(x)\,\mathrm{d}x=\int h(g(t))g'(t)\,\mathrm{d}t.
\end{gathered}
\tag{4.8}\] Bei geschickter Wahl der Funktion \(g(t)\) kann das Integral auf der rechten Seite von (4.8) erheblich einfacher sein, als das Integral auf der linken Seite.
Wir probieren das am besten einmal aus mit einem klassischen Lehrbuchbeispiel.
Musteraufgabe 4.17
Man bestimme eine Stammfunktion von \(f(x)=2xe^{x^2}\).
Man berechne \(\displaystyle\int_0^3 f(x)\,\mathrm{d}x\).
Lösung: Wir setzen \(x^2 =t\) und erhalten so die Substitution\[
\begin{gathered}
x=\sqrt{t}=g(t),\qquad g'(t)=\frac{1}{2\sqrt{t}}.
\end{gathered}
\] Das setzen wir nun ein: \[
\begin{aligned}
\int 2xe^{x^2}\,\mathrm{d}x&=\int 2\sqrt{t}\cdot e^t\cdot
\frac{1}{2\sqrt{t}} \,\mathrm{d}t.
\end{aligned}
\] Der Term \(2\sqrt{t}\) kürzt sich aber, sodass wir sofort eine Stammfunktion angeben können: \[
\begin{gathered}
\int 2xe^{x^2}\,\mathrm{d}x=\int 2\sqrt{t}\cdot e^t\cdot
\frac{1}{2\sqrt{t}} \,\mathrm{d}t =\int e^t\,\mathrm{d}t = e^t+C
\end{gathered}
\] Aber \(t\) war eine nur vorübergehend gebrauchte Abkürzung für \(x^2\). Als letzten Schritt resubstituieren wir \(t=x^2\) und haben schließlich ohne Mühe gefunden: \[
\begin{gathered}
\int 2xe^{x^2}\,\mathrm{d}x=e^{x^2}+C.
\end{gathered}
\] Zum Abschluss setzen wir noch die Integrationsgrenzen sein: \[
\begin{gathered}
\int_0^3 f(x)\,\mathrm{d}x=e^{x^2}\Big|_0^3=e^9-1
=8102.08\,.
\end{gathered}
\] □
Musteraufgabe 4.18
Man bestimme eine Stammfunktion von \(f(x)=\dfrac{x}{1+x^2}\).
Man berechne \(\displaystyle\int_{-2}^3 f(x)\,\mathrm{d}x\).
Lösung: Wir setzen \(1+x^2 =t\) und erhalten so die Substitution\[
\begin{gathered}
x=\sqrt{t-1}=g(t),\qquad g'(t)=\frac{1}{2\sqrt{t-1}}.
\end{gathered}
\] Diese Substitution ergibt: \[
\begin{aligned}
\int \frac{x}{1+x^2}\,\mathrm{d}x&=\int \frac{\sqrt{t-1}}{t} \cdot
\frac{1}{2\sqrt{t-1}}\,\mathrm{d}t=\frac{1}{2}\int
\frac{1}{t}\,\mathrm{d}t =\frac{1}{2}\ln t+C.
\end{aligned}
\] Resubstitution \(t=1+x^2\) liefert endlich: \[
\begin{gathered}
\int \frac{x}{1+x^2}\,\mathrm{d}x=\frac{1}{2}\ln(1+x^2)+C.
\end{gathered}
\] Das bestimmte Integral hat den Wert: \[
\begin{gathered}
\int_{-2}^3f(x)\,\mathrm{d}x=\frac{1}{2}\ln(1+x^2)\Big|_{-2}^3
=\frac{1}{2}\ln 10 -\frac{1}{2}\ln 5=0.3466\,.
\end{gathered}
\] □
Die eben beschriebene Methode ist immer dann besonders einfach anwendbar, wenn die innere Funktion eine lineare Funktion ist, d.h. wenn wir suchen: \[
\begin{gathered}
\int h(ax+b)\,\mathrm{d}x.
\end{gathered}
\] Wir wählen die Substitution \(ax+b=t\), das ergibt: \[
\begin{gathered}
ax+b=t\implies x=\frac{t}{a}-\frac{b}{a}=g(t)\quad\text{mit}
\quad g'(t)=\frac{1}{a}.
\end{gathered}
\] Wenn \(H\) eine Stammfunktion von \(h\) ist, dann liefert die Kettenregel (4.8): \[
\begin{gathered}
\int h(ax+b)\,\mathrm{d}x=\int
h(t)\cdot\frac{1}{a}\,\mathrm{d}t=\frac{1}{a}\cdot H(t)+C.
\end{gathered}
\] Dieses Ergebnis ist so häufig anwendbar, dass wir es besonders hervorheben:
Lösung: Der einzige Unterschied zu Musteraufgabe 4.21 ist die äußere Funktion \(h\). Nun haben wir \(h(t)=\dfrac{1}{t^3}\) mit \(H(t)=
-\dfrac{1}{2t^2}\). Daher: \[
\begin{aligned}
\int \frac{1}{(2x+1)^3}\,\mathrm{d}x & = \frac{1}{2}H(2x+1)+C =-\frac{1}{4}\,\frac{1}{(2x+1)^2}+C,\\[2ex]
\int_1^2 \frac{1}{(2x+1)^3}\,\mathrm{d}x & = -\frac{1}{4}\,\frac{1}{(2x+1)^2}\Bigg|_1^2 \\
& =-\frac{1}{4}\left(\frac{1}{25}-\frac{1}{9}\right)=\frac{4}{225}=0.0178\,.
\end{aligned}
\] □
Lösung: Wir setzen \(3+\sqrt{x+8}=t\). Dies liefert: \[
\begin{gathered}
x=(t-3)^2-8 = g(t),\quad g'(t)=2(t-3).
\end{gathered}
\] Und weiter: \[
\begin{aligned}
\int\frac{1}{3+\sqrt{x+8}}\,\mathrm{d}x & =\int\frac{1}{t}\cdot 2(t-3)\,\mathrm{d}t
= 2\int 1\,\mathrm{d}t-6\int\frac{1}{t}\,\mathrm{d}t \\[4pt]
& = 2t-6\ln t+C \\
& = 2(3+\sqrt{x+8})-6\ln(3+\sqrt{x+8})+C.
\end{aligned}
\] Schließlich setzen wir noch die Integrationsgrenzen ein: \[
\begin{gathered}
\int_0^1\frac{1}{3+\sqrt{x+8}}\,\mathrm{d}x=2(3+\sqrt{x+8})-6\ln(3+\sqrt{x+8})
\bigg|_0^1=0.1691\,.
\end{gathered}
\] □
4.3 Anwendungen von Integralen
Integrale spielen in vielen Bereichen der angewandten Mathematik eine zentrale Rolle. Im Folgenden geben wir einen kurzen Überblick über einige wichtige Anwendungen.
4.3.1 Flächeninhalte
Die populärste Anwendung von Integralen betrifft die Messung von Flächeninhalten. Dieses Quadraturproblem stand bereits ganz am Anfang unserer Überlegungen in diesem Kapitel.
Es sei \(f(x)\) eine Funktion und es bezeichne \(A(x)\) den Flächeninhalt unter dem Funktionsgraphen entlang des Intervalls \([0,x]\). Dann ist \[
\begin{gathered}
A(x+h)-A(x)\approx f(x)h,
\end{gathered}
\] und daraus folgt für \(h\to 0\), dass \(A'(x)=f(x)\). Der Flächeninhalt \(A(x)\) ist also eine Stammfunktion von \(f(x)\). Daher muss die Gleichung \[
\begin{gathered}
A(b)-A(a)=\int_a^b f(x)\,\mathrm{d}x
\end{gathered}
\] richtig sei, siehe Abbildung 4.3.
Abbildung 4.3: Integral als Flächeninhalte.
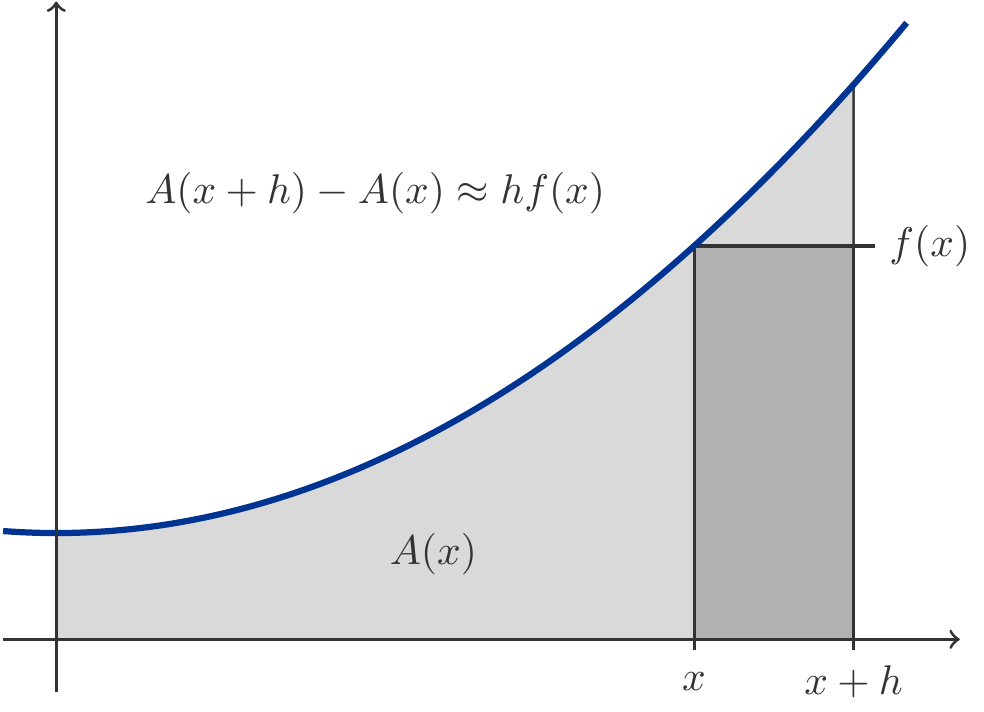
Wir fassen zusammen: Der (orientierte) Flächeninhalt unter einem Funktionsgraphen ist identisch mit dem bestimmten Integral der Funktion.
Abbildung 4.4: Orientierter Flächeninhalt.
Musteraufgabe 4.25 Man berechne den Flächeninhalt unter der Funktion \(f(x)=e^{-2x}\) zwischen den Grenzen \(x=0\) und \(x=10\).
Unter dem Durchschnittswert\(\bar{f}\) einer Funktion \(f\) auf einem Intervall \([a,b]\) versteht man die Höhe eines Rechtecks über dem Intervall, das den gleichen Flächeninhalt einschließt wie der Funktionsgraph. Das bedeutet \[
\begin{gathered}
\bar{f}(b-a)=\int_a^b f(x)\,\mathrm{d}x\quad\implies\quad
\bar{f}=\frac{1}{b-a} \int_a^b f(x)\,\mathrm{d}x
\end{gathered}
\tag{4.10}\] Die Beziehung (4.10) wird auch Mittelwertsatz der Integralrechnung genannt.
Abbildung 4.5: Durchschnittswert einer Funktion.
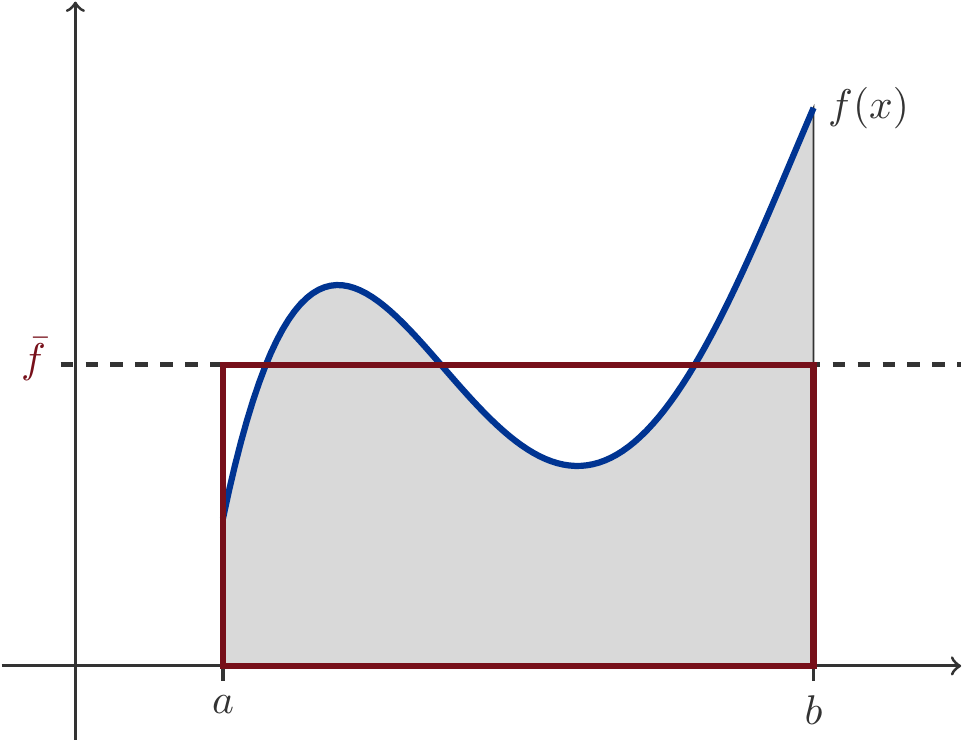
Musteraufgabe 4.26
Berechne den Durchschnittswert von \(f(x)=x\) auf dem Intervall \([0,5]\).
Berechne den Durchschnittswert von \(f(x)=e^{-x}\) auf dem Intervall \([0,5]\).
In vielen Anwendungen, z.B. der Lagerhaltungstheorie oder der Theorie der Warteschlangen, spielen stückweise lineare Funktionen und deren Durchschnittswerte eine Rolle.
Ein Beispiel ist die Funktion \(f(x)\) gegeben durch: \[
\begin{gathered}
f(x)=\left\{\begin{array}{cl}
2 & 0\le x < 3\\
4 & 3\le x < 6\\
3 & 6\le x < 7\\
5 & 7\le x < 9
\end{array}\right.
\end{gathered}
\] Wir können uns vorstellen, dass \(x\) die Zeit und \(f(x)\) die Anzahl von wartenden Kunden zur Zeit \(x\) bezeichnet. Was ist dann die durchschnittliche Länge der Warteschlange?
Der Graph der Funktion \(f(x)\) ist in Abbildung 4.6 dargestellt.
Diese Funktion besitzt Unstetigkeitsstellen in \(x=3\), \(x=6\) und \(x=7\). Ihr Durchschnittswert \(\bar{f}\) ist \[
\begin{gathered}
\bar{f}=\frac{1}{9}\int_0^9f(x)\,\mathrm{d}x.
\end{gathered}
\]
Abbildung 4.6: Die stückweise lineare Funktion von Beispiel 4.27.
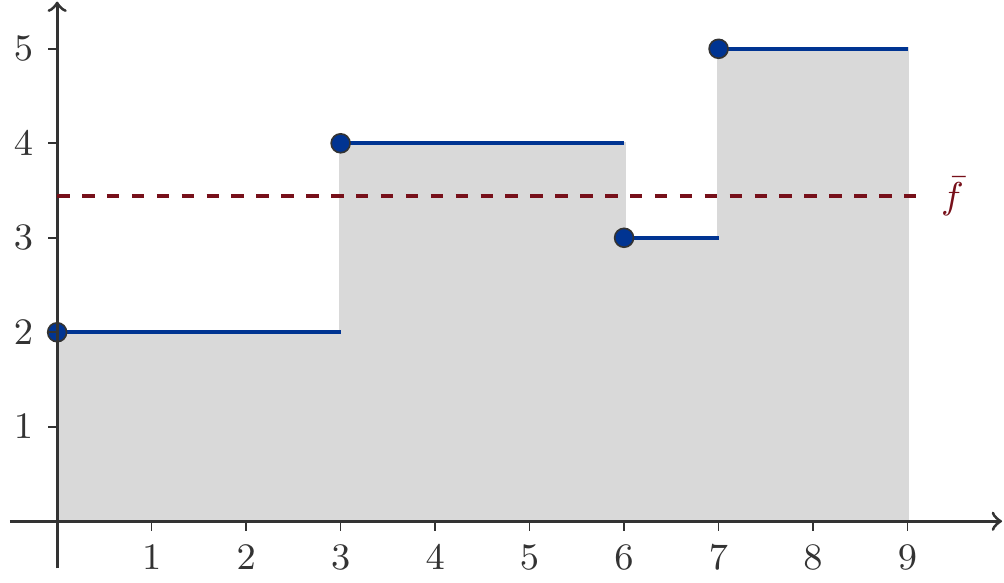
Aber wir berechnen wir dieses Integral? Dazu verwenden wir die Additivitätseigenschaft aus Satz 4.6: \[
\begin{aligned}
\bar{f}&=\frac{1}{9}\left[\int_0^32\,\mathrm{d}x+
\int_3^64\,\mathrm{d}x+\int_6^73\,\mathrm{d}x+\int_7^95\,\mathrm{d}x\right]=\\[5pt]
&=\frac{1}{9}\left[2x\big|_0^3+4x\big|_3^6+3x\big|_6^7+5x\big|_7^9\right]\\
&=\frac{1}{9}\left[2\cdot 3+4\cdot(6-3)+3\cdot(7-6)+5\cdot(9-7)\right]
=\frac{31}{9}\simeq 3.44\,.
\end{aligned}
\] Würde \(f(x)\) die Länge einer Warteschlange über das Zeitintervall \([0,9]\) beschreiben, dann hätte diese Warteschlange die mittlere Länge von 3.44 Kunden.
4.3.3 Lagerhaltung
In Kapitel 3 haben wir uns bereits etwas mit Lagerhaltung beschäftigt und dabei in recht informeller Weise die klassische Lagerhaltungsformel für das einfachste Modell, Economic Order Quantity, hergeleitet.
Wir erinnern uns, dass es in diesem einfachen Modell im Wesentlichen drei Anknüpfungspunkte für Kosten gibt: (a) die Anzahl der Bestellvorgänge pro Zeiteinheit, (b) die Anschaffungskosten der gelagerten Ware und (c) der mittlere Lagerbestand. Im EOQ-Modell ist letzterer exakt die Hälfte der optimalen Bestellmenge \(x^\ast\) (siehe Abbildung 3.16).
Wir wollen nun klären, warum wir argumentieren dürfen, dass die Kosten der physischen Lagerung proportional dem mittleren Lagerbestand sind.
Die Lagerung eines Gutes kostet \(h\) GE pro Zeiteinheit und Mengeneinheit. Die Lagerhöhe ist veränderlich und durch die Funktion \(I(t)\) gegeben. Wie kann man die Kosten für die Lagerung berechnen?
Wir bezeichnen die Kosten, die für die Lagerung im Zeitintervall \([0,t]\) anfallen, mit \(C(t)\). Der Lagerbestand ändert sich typischerweise in der Zeit, aber für sehr kleine Zeitintervalle \([t,t+\epsilon]\), können wir unterstellen, dass die gelagerte Menge \(I(t)\) annähernd gleich bleibt. Dann gilt \[
\begin{gathered}
C(t+\epsilon)-C(t)\approx hI(t)\epsilon\quad\text{oder}\quad
\frac{C(t+\epsilon)-C(t)}{\epsilon}\approx hI(t)\;.
\end{gathered}
\] Für \(\epsilon\to 0\) ist daher \[
\begin{gathered}
C'(t)=hI(t),
\end{gathered}
\] die Lagerkosten sind also eine Stammfunktion der Funktion \(hI(t)\), und deshalb: \[
\begin{gathered}
C(T)=h\int_0^T I(t)\,\mathrm{d}t.
\end{gathered}
\] Bedenkt man, dass wegen des Mittelwertsatzes (4.10) \[
\begin{gathered}
\bar{I}=\frac{1}{T}\int_0^T I(t)\,\mathrm{d}t
\end{gathered}
\] den durchschnittlichen Lagerbestand ausdrückt, dann lautet die Formel für die Lagerkosten \[
\begin{gathered}
C(T)=hT\bar{I},\quad\text{für alle }T\ge 0.
\end{gathered}
\] Man kann also die Lagerkosten immer so berechnen, dass man ein konstantes Lager in der Höhe des durchschnittlichen Lagerbestandes unterstellt.
Musteraufgabe 4.28 Im Zeitintervall \((0,10)\) ist eine Lagerbestandsfunktion \(I(t)\) gegeben durch: \[
\begin{gathered}
I(t)=\left\{\begin{array}{ll}
-t+4 & 0\le t<3\\
-t+8 & 3\le t < 5\\
-t+12 & 5\le t< 10
\end{array}\right.
\end{gathered}
\] Wie hoch ist der durchschnittliche Lagerbestand \(\bar{I}\)?
Lösung: Die Funktion ist recht ähnlich jener, die uns schon in Abbildung 3.15 begegnet ist. Ihr Graph ist in Abbildung 4.7 zu sehen.
Abbildung 4.7: Die Lagerbestandsfunktion \(I(t)\) aus Musteraufgabe 4.28.
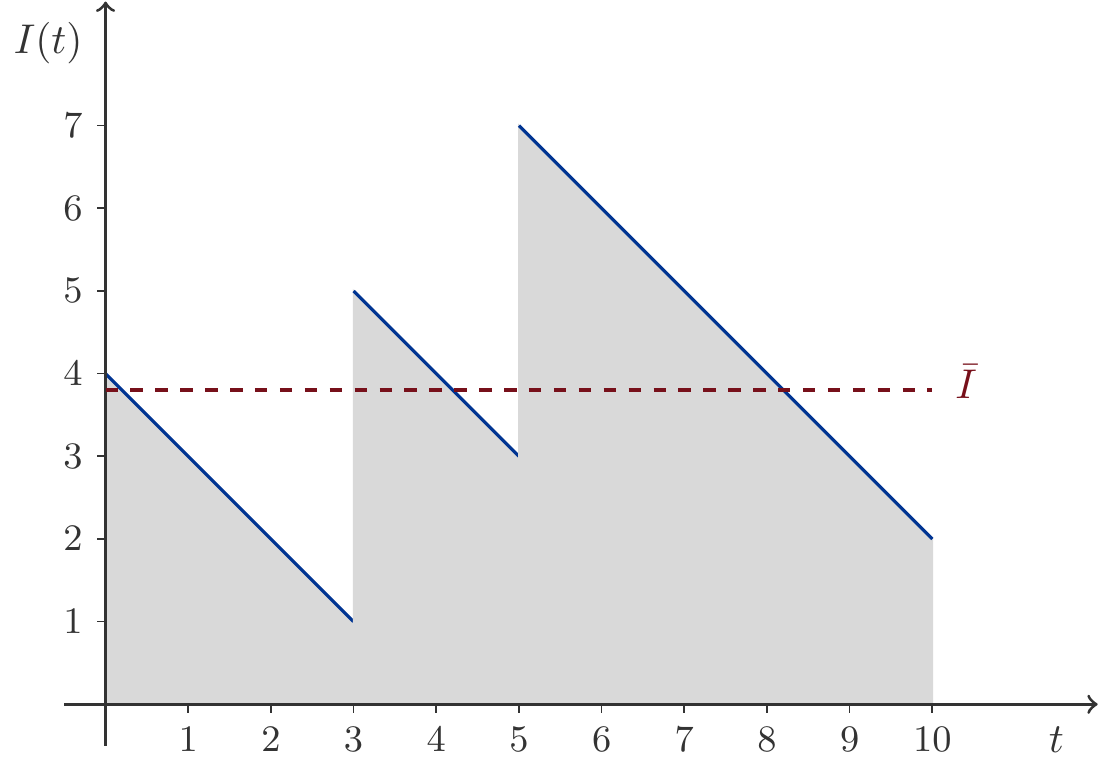
Für den mittleren Lagerbestand errechnen wir: \[
\begin{aligned}
\bar{I}&=\frac{1}{10}\left[\int_0^3(-t+4)\,\mathrm{d}t+\int_3^5(-t+8)\,\mathrm{d}t
+ \int_5^{10}(-t+12)\,\mathrm{d}t\right]\\[5pt]
&=\frac{1}{10}\left[
\left(-\frac{t^2}{2}+4t\right)\bigg|_0^3
+\left(-\frac{t^2}{2}+8t\right)\bigg|_3^5
+\left(-\frac{t^2}{2}+12t\right)\bigg|_5^{10}
\right]\\[5pt]
&=\frac{38}{10}=3.8\,.
\end{aligned}
\]
Musteraufgabe 4.29
Wie hoch ist der durchschnittliche Lagerbestand, wenn die Lagerhöhe bei \(L(0)=1000\) beginnt, gleichmäßig (linear) abnimmt und bei \(L(10)=500\) endet?
Wie hoch ist der durchschnittliche Lagerbestand, wenn die Lagerhöhe bei \(L(0)=1000\) beginnt, mit einer konstanten relativen Rate abnimmt und bei \(L(10)=500\) endet?
Lösung: (1) Lineare Abnahme bedeutet \(L(t) = a-bt\) mit \[
\begin{gathered}
L(0)=1000,\quad L(10)=500\implies
L(t)=1000-50t.
\end{gathered}
\] Der durchschnittliche Bestand ist daher: \[
\begin{gathered}
\bar{L}=\frac{1}{10}\int_0^{10}(1000-50t)\,dt=750.
\end{gathered}
\]
(2) Abnahme mit konstanter relativer Rate bedeutet \(L(t)=L(0)e^{-at}\) mit \[
\begin{gathered}
L(0)=1000, \quad L(10)=500\implies L(t)
=1000e^{-0.0693 t}.
\end{gathered}
\] Der durchschnittliche Bestand beträgt nun: \[
\begin{gathered}
\bar{L}=\frac{1}{10}\int_0^{10}1000e^{-0.0693t}\,dt=721.35\,.
\end{gathered}
\] □
4.3.4 Kontinuierliche Zahlungsströme
Die Interpretation von bestimmten Integralen in Zusammenhang mit kontinuierlichen Zahlungsströmen haben wir schon besprochen.
Musteraufgabe 4.30 Ein Kapital in der Höhe von 1000 GE wird mit der Rate \(a(t)=3-0.1
t\) erhöht. Wie hoch ist das Kapital nach 10 Perioden?
Lösung: Aus der Problemstellung folgt, dass die Änderungsrate des Kapitals \(K'(t)=a(t)=3-0.1t\). Daher gilt wegen (4.2): \[
\begin{aligned}
K(10)&=K(0)+\int_0^{10} a(t)\,\mathrm{d}t=1000+\int_0^{10} (3-0.1t)\,\mathrm{d}t\\
&=1000+(3t-0.05t^2)\Big|_0^{10}=1000+30-5=1025.
\end{aligned}
\] □
In der Regel unterliegen kontinuierliche Zahlungsströme auch einer Verzinsung wie finanzmathematische Renten.
Endwert und Barwert von Zahlungsströmen
Es sei \(K(0)\) ein Kapital, das mit dem nominellen Zinssatz \(c\) kontinuierlich verzinst wird und dem neues Kapital mit der Rate \(a(t)\) zufließt. Die Bezeichnung \(a(t)\) für den Kapitalzufluß ist nicht zufällig gewählt. In Kapitel 2 haben wir mit \(a\) die Zahlungen einer Rente bezeichnet, die dort allerdings als konstant vorausgesetzt wurden. Nun werden wir allgemeiner zulassen, dass die Zahlungen explizit von der Zeit abhängen.
Wir wollen berechnen, auf welchen Endwert das Kapital nach der Zeit \(T\) angewachsen ist.
Die Änderungsrate des Kapitals durch die Verzinsung allein würde \(K'(t)=cK(t)\) betragen, denn der nominelle Zinssatz ist ja die relative Änderungsrate des Kapitals, also \(K'(t)/K(t)=c\). Wenn wir beide Quellen der Vermögensänderung berücksichtigen, ergibt sich als totale Änderungsrate des Kapitals: \[
\begin{gathered}
K'(t)=cK(t)+a(t).
\end{gathered}
\tag{4.11}\] Das ist eine Differentialgleichung. Solche Gleichungen sind im allgemeinen außerordentlich schwer zu lösen. Hier haben wir aber zum Glück eine vergleichsweise einfache Situation vor uns.
Um die unbekannte Funktion \(K(t)\) zu finden, multiplizieren wir beide Seiten von (4.11) mit dem Faktor \(e^{-ct}\). Kurz, wir zinsen ab, gehen zu Barwerten über. Nach Umstellen entdecken wir etwas Interessantes: \[
\begin{gathered}
\underbrace{e^{-ct}K'(t)-ce^{-ct}K(t)}_{(e^{-ct}K(t))'}=e^{-ct}a(t).
\end{gathered}
\] Die linke Seite ergibt sich durch Anwenden der Produktregel auf den Barwert des Kapitals \(e^{-ct}K(t)\): \[
\begin{gathered}
\Big( e^{-ct}K(t)\Big)'=e^{-ct}a(t).
\end{gathered}
\] Die rechte Seite ist der Barwert der Zahlung zur Zeit \(t\). Also ist \(e^{-ct}K(t)\) eine Stammfunktion von \(e^{-ct}a(t)\) und wir können sagen: \[
\begin{gathered}
e^{-cT}K(T)=K(0)+\int_0^T e^{-ct} a(t)\,\mathrm{d}t.
\end{gathered}
\tag{4.12}\] Dies ist tatsächlich eine Formel für den Barwert einer kontinuierlichen Rente mit Anfangskapital \(K(0)\).
Abgesehen vom Anfangswert \(K(0)\) ist (4.12) strukturgleich mit der Barwertformel (2.11) aus Kapitel 2: der Barwert des Zahlungsstroms ist die Summe der abgezinsten Zahlungen, wobei hier Summe eben Integral bedeutet2.
Wenn wir (4.12) aufzinsen, d.h. beide Seiten dieser Gleichung mit dem Aufzinsungsfaktor \(e^{cT}\) multiplizieren, dann erhalten wir eine Endwertformel: \[
\begin{gathered}
K(T)=e^{cT}K(0)+\int_0^T e^{c(T-t)}a(t)\,\mathrm{d}t.
\end{gathered}
\tag{4.13}\] Diese Formel ist, abgesehen vom Anfangskapital, analog zu (2.13): der Endwert eines kontinuierlichen Zahlungsstroms ergibt sich aus dem Endwert des Anfangskapitals plus der (kontinuierlichen) Summe der über die Restlaufzeit \(T-t\) aufgezinsten Zahlungen \(e^{c(T-t)}a(t)\).
Musteraufgabe 4.31 Wie hoch ist der Endwert eines Zahlungsstroms mit der konstanten Rate \(a(t)=2000\) und dem Zinssatz \(c=0.05\) nach 10 Jahren?
Lösung: Da hier kein Anfangskapital angegeben ist, dürfen wir \(K(0)=0\) annehmen. Nun wenden wir (4.13) an: \[
\begin{gathered}
K(10)=\int_0^{10}e^{0.05(10-t)}2000\,\mathrm{d}t
=2000e^{0.5}\int_0^{10}e^{-0.05t}\,\mathrm{d}t
=25948.85\,.
\end{gathered}
\] Das letzte Integral ist aber sehr einfach mit Hilfe von Satz 4.19 zu berechnen: \[
\begin{gathered}
\int_0^Te^{-ct}\,\mathrm{d}t=-\frac{1}{c}\,e^{-ct}\bigg|_0^T=\frac{1-e^{-cT}}{c}\,.
\end{gathered}
\tag{4.14}\] In unserem Beispiel: \[
\begin{gathered}
\int_0^{10}e^{-0.05t}\,\mathrm{d}t=\frac{1-e^{-0.05\cdot 10}}{0.05}=7.86938681,
\end{gathered}
\] und somit: \[
\begin{gathered}
K(10)=2000\cdot e^{0.5}\cdot 7.86938681=25948.85085\simeq 25949.
\end{gathered}
\] □
Musteraufgabe 4.32 Welcher konstante Zahlungsstrom \(a\) muss einem Sparguthaben zugeführt werden, damit es nach 8 Jahren die Höhe von 10000 GE erreicht (nomineller Zinssatz 4 Prozent)?
Lösung: Wir wenden die Endwertformel (4.13) mit \(K(0)=0\) an. Dann muss der Zahlungsstrom \(a\) den Endwert \[
\begin{gathered}
10000=\int_0^8 e^{0.04(8-t)}a\,\mathrm{d}t = a\cdot
e^{0.32}\int_0^8e^{-0.04t}\,\mathrm{d}t
\end{gathered}
\] produzieren. Wir berechnen das Integral mittels (4.14): \[
\begin{gathered}
\int_0^8e^{-0.04t}\,\mathrm{d}t=\frac{1-e^{-0.04\cdot
8}}{0.04}=6.84627407\,.
\end{gathered}
\] Also ist \[
\begin{gathered}
a=\frac{10000}{e^{0.32}\cdot 6.84627407}=1060.648507\simeq 1061\,.
\end{gathered}
\] □
Musteraufgabe 4.33 Wie hoch muss eine konstante Tilgungsrate sein, damit eine Schuld von 50000 GE nach 10 Jahren getilgt ist (nomineller Zinssatz 5 Prozent)?
Lösung: Die konstante Tilgungsrate \(a\) muss den Endwert \[
\begin{gathered}
0=50000e^{0.05\cdot10}+\int_0^{10} e^{0.05(10-t)}(-a)\,\mathrm{d}t
\end{gathered}
\] ergeben. Indem wir durch den Aufzinsungsfaktor \(e^{0.05\cdot10}\) dividieren, also zu Barwerten übergehen, erhalten wir die einfachere Gleichung: \[
\begin{gathered}
0=50000-a\int_0^{10} e^{-0.05t}\,\mathrm{d}t.
\end{gathered}
\] Das Integral haben wir bereits in der Lösung von Musteraufgabe 4.31 berechnet: \[
\begin{gathered}
a=\frac{50000}{7.86938681}=6353.735205\simeq 6354.
\end{gathered}
\] □
Musteraufgabe 4.34 Wie hoch muss eine gleichmäßig gegen Null fallende Tilgungsrate anfänglich sein sein, damit eine Schuld von 50000 GE nach 10 Jahren getilgt ist (nomineller Zinssatz 5 Prozent)?
Lösung: Wenn die Tilgungsrate \(a(t)\) mit Anfangswert \(a_0\) gleichmäßig, d.h. linear, in 10 Jahren gegen Null fällt, dann muss \(a(t)\) die Gleichung erfüllen: \[
\begin{gathered}
a(t)=a_0\left(1-\frac{t}{10}\right).
\end{gathered}
\] Diese Tilgungsrate muss den Endwert \[
\begin{gathered}
0=50000e^{0.05\cdot10}-\int_0^{10}
e^{0.05(10-t)}a_0\left(1-\frac{t}{10}\right)\,\mathrm{d}t
\end{gathered}
\] produzieren. Indem wir wieder durch den Aufzinsungsfaktor dividieren, also zu Barwerten übergehen, erhalten wir: \[
\begin{gathered}
0=50000-a_0\int_0^{10} e^{-0.05t}\left(1-\frac{t}{10}\right)\,\mathrm{d}t,
\end{gathered}
\] das liefert den anfänglichen Wert der Tilgungsrate: \[
\begin{gathered}
a_0=\frac{50000}{\int_0^{10}
e^{-0.05t}\left(1-\frac{t}{10}\right)\,\mathrm{d}t }\,.
\end{gathered}
\] Das Integral auf der rechten Seite erfordert nun etwas mehr Arbeit. Wir zerlegen es in zwei Teile: \[
\begin{aligned}
I&=\int_0^{10} e^{-0.05t}\left(1-\frac{t}{10}\right)\,\mathrm{d}t\\[5pt]
&=\int_0^{10}e^{-0.05t}\,\mathrm{d}t-\frac{1}{10}\int_0^{10}
t\cdot e^{-0.05t}\,\mathrm{d}t.
\end{aligned}
\] Das erste Integral haben wir in den letzten Aufgaben mehrfach berechnet, sein Wert ist konkret \(7.86938681\), allgemein aber (4.14). Das zweite Integral müssen wir mittels partieller Integration berechnen (Satz 4.13): \[
\begin{gathered}
\int_0^T t\cdot
e^{-ct}\,\mathrm{d}t=\frac{-(1+ct)e^{-ct}}{c^2}\bigg|_0^T=\frac{1-(1+cT)e^{-cT}}{c^2}\,.
\end{gathered}
\] Daraus errechnen wir für die gegenständliche Aufgabe: \[
\begin{gathered}
\int_0^{10}t\cdot e^{-0.05t}\,\mathrm{d}t=\frac{1-(1+0.05\cdot
10)e^{-0.05\cdot 10}}{0.05^2}=36.0816042\,.
\end{gathered}
\] Also ist \[
\begin{gathered}
I=7.86938681-\frac{36.0816042}{10}= 4.26122639\,.
\end{gathered}
\] Das ergibt schließlich den anfänglichen Wert \(a_0\) der Tilgungsrate: \[
\begin{gathered}
a_0=\frac{50000}{\int_0^{10} e^{-0.05t}(1-t/10)\,dt} =
\frac{50000}{4.26122639}=
11733.71124.
\end{gathered}
\] □
4.4 Weitere Übungsaufgaben
Bestimmen Sie für \[
\begin{gathered}
f(x)=3x^3-20x^2+5x-10
\end{gathered}
\] eine Stammfunktion \(F(x)\) so, dass \(F(0)=38\). Welchen Wert hat \(F(6)\)?
Lösung:\(F(6)=-400\).
Ein Unternehmen produziert mit Grenzkosten \[
\begin{gathered}
C'(x)=3x^2-6x+14,\quad x=\text{ Output}.
\end{gathered}
\] Bei einem Output von 10 Einheiten betragen die Gesamtkosten 2840 GE. Wie hoch sind die Gesamtkosten bei einem Output von 20 Mengeneinheiten?
Lösung:\(C(20)=9080\)
Berechnen Sie \(I=\int_1^2 f(x)\,\mathrm{d}x\) mit \(\displaystyle
f(x)=-3x^2+5+\frac{4}{x^2}\).
Welchen Durchschnittswert hat die Funktion \(f(x)=x^2-2x+5\) im Intervall \((-1,1)\)?
Lösung:\(\bar{f}=16/3\).
Welchen Durchschnittswert hat die Funktion \(f(x)=e^{-x/4}\) im Intervall \((1,10)\)?
Lösung:\(\bar{f}=0.3097\).
Welchen Durchschnittswert hat die Funktion \(f(x)=\ln x\) im Intervall \((1,100)\)?
Lösung:\(\bar{f}=3.6517\).
Wie hoch ist der durchschnittliche Lagerbestand, wenn die Lagerhöhe bei \(L(0)=4046\) beginnt, gleichmäßig (linear) abnimmt und bei \(L(16)=2354\) endet?
Lösung:\(\bar{I}=3200\).
Wie hoch ist der durchschnittliche Lagerbestand, wenn die Lagerhöhe bei \(L(0)=6556\) beginnt, mit einer konstanten relativen Rate abnimmt und bei \(L(8)=1423\) endet? Runden Sie das Ergebnis auf eine ganze Zahl.
Lösung:\(\bar{I}=3360\).
Eine Lagerbestandsfunktion ist gegeben durch: \[
\begin{gathered}
I(t)=\left\{\begin{array}{cl}
3 & 0\le t< 2\\
5 & 2\le t < 5\\
2 & 5\le t<8
\end{array}\right.
\end{gathered}
\] Berechnen Sie den mittleren Lagerbestand.
Lösung:\(\bar{I}=27/8=3.375\)
Eine Lagerbestandsfunktion ist gegeben durch: \[
\begin{gathered}
I(t)=\left\{\begin{array}{cl}
-\frac{t}{2}+2 & 0\le t< 2\\[4pt]
-\frac{t}{2}+4 & 2\le t < 3
\end{array}\right.
\end{gathered}
\] Berechnen Sie den mittleren Lagerbestand.
Lösung:\(\bar{I}=23/12=1.92\)
Ein Kapital in der Höhe von 2000 GE wird mit der Rate \(a(t)=11-0.14t\) erhöht. Wie hoch ist das Kapital nach 35 Perioden? Runden Sie das Ergebnis auf eine ganze Zahl.
Lösung: 2299.25 GE
Wie hoch ist der Endwert eines Zahlungsstroms mit konstanter Rate \(a(t)=3300\) und dem Zinssatz \(c=0.09\) nach 4 Jahren? Runden Sie das Ergebnis auf eine ganze Zahl.
Lösung: 15889 GE
Welcher konstante Zahlungsstrom ist erforderlich, damit ein Sparguthaben nach 7 Jahren die Höhe von 14900 GE erreicht. Rechnen Sie mit einem nominellen Zinssatz von 10 Prozent und runden Sie das Ergebnis auf eine ganze Zahl.
Lösung: 1470 GE
Wie hoch muss eine konstante Tilgungsrate sein, damit eine Schuld von 19000 GE nach 5 Jahren getilgt ist? Rechnen Sie mit einem nominellen Zinssatz von 6 Prozent und runden Sie das Ergebnis auf eine ganze Zahl.
Lösung: 4398 GE
Wie hoch muss eine gleichmäßig gegen Null fallende Tilgungsrate anfänglich sein, damit eine Schuld von 11000 GE nach 6 Jahren getilgt ist? Rechnen Sie mit einem nominellen Zinssatz von 6 Prozent und runden Sie das Ergebnis auf eine ganze Zahl.
