8 Analysis von Funktionen mit zwei Variablen
![]()
Die erste Ableitung
Bestimmen Sie die partielle Ableitung \(f'_1(x_1,x_2)\) der Funktion \[\begin{aligned} f(x_1, x_2) = 125 x_1^{0.17} x_2^{0.83} \end{aligned}\] an der Stelle \(\mathbf{a} = \left( \begin{array}{c} 5.2 \\ 5.1 \end{array} \right)\).
1. Schritt: Ermittlung der partiellen Ableitung \(f'_1(x_1,x_2)\) \[\begin{aligned} f'_1(x_1,x_2) = 125 \cdot 0.17 \cdot x_1^{-0.83} x_2^{0.83} \end{aligned}\] 2. Schritt: Einsetzen von \(\mathbf{a} = \left( \begin{array}{c} 5.2 \\ 5.1 \end{array} \right)\) in die partielle Ableitung \(f'_1(x_1,x_2)\) \[\begin{aligned} f'_1(5.2,5.1) = 125 \cdot 0.17 \cdot 5.2^{-0.83} 5.1^{0.83} = 20.910259 \approx 20.91 \end{aligned}\]
Bestimmen Sie die partielle Ableitung \(f'_1(x_1,x_2)\) der Funktion \[\begin{aligned} f(x_1, x_2) = 108 x_1^{0.27} x_2^{0.73} \end{aligned}\] an der Stelle \(\mathbf{a} = \left( \begin{array}{c} 6.5 \\ 5.8 \end{array} \right)\).
1. Schritt: Ermittlung der partiellen Ableitung \(f'_1(x_1,x_2)\) \[\begin{aligned} f'_1(x_1,x_2) = 108 \cdot 0.27 \cdot x_1^{-0.73} x_2^{0.73} \end{aligned}\] 2. Schritt: Einsetzen von \(\mathbf{a} = \left( \begin{array}{c} 6.5 \\ 5.8 \end{array} \right)\) in die partielle Ableitung \(f'_1(x_1,x_2)\) \[\begin{aligned} f'_1(6.5,5.8) = 108 \cdot 0.27 \cdot 6.5^{-0.73} 5.8^{0.73} = 26.832628 \approx 26.83 \end{aligned}\]
Bestimmen Sie die partielle Ableitung \(f'_1(x_1,x_2)\) der Funktion \[\begin{aligned} f(x_1, x_2) = 53 x_1^{0.8} x_2^{0.2} \end{aligned}\] an der Stelle \(\mathbf{a} = \left( \begin{array}{c} 0.4 \\ 4.8 \end{array} \right)\).
1. Schritt: Ermittlung der partiellen Ableitung \(f'_1(x_1,x_2)\) \[\begin{aligned} f'_1(x_1,x_2) = 53 \cdot 0.8 \cdot x_1^{-0.2} x_2^{0.2} \end{aligned}\] 2. Schritt: Einsetzen von \(\mathbf{a} = \left( \begin{array}{c} 0.4 \\ 4.8 \end{array} \right)\) in die partielle Ableitung \(f'_1(x_1,x_2)\) \[\begin{aligned} f'_1(0.4,4.8) = 53 \cdot 0.8 \cdot 0.4^{-0.2} 4.8^{0.2} = 69.695078 \approx 69.70 \end{aligned}\]
Bestimmen Sie die partielle Ableitung \(f'_2(x_1,x_2)\) der Funktion \[\begin{aligned} f(x_1, x_2) = -20 \cdot \ln \left (x_1 \right ) -15 \cdot \ln \left (x_2 \right ) \end{aligned}\] an der Stelle \(\mathbf{a} = \left( \begin{array}{c} 4 \\ 5 \end{array} \right)\).
1. Schritt: Ermittlung der partiellen Ableitung \[\begin{aligned} f'_2(x_1, x_2) & = & -15 \cdot \frac{1}{x_2} \end{aligned}\]
2.Schritt: Einsetzen von \(\mathbf{a} = \left( \begin{array}{c} 4 \\ 5 \end{array} \right)\) in die partielle Ableitung \[\begin{aligned} f'_2(4, 5) & = & \frac{-15}{5} = -3 \end{aligned}\]
Bestimmen Sie die partielle Ableitung \(f'_2(x_1,x_2)\) der Funktion \[\begin{aligned} f(x_1, x_2) = 50 \cdot \ln \left (x_1 \right ) + 40 \cdot \ln \left (x_2 \right ) \end{aligned}\] an der Stelle \(\mathbf{a} = \left( \begin{array}{c} 5 \\ 3 \end{array} \right)\).
1. Schritt: Ermittlung der partiellen Ableitung \[\begin{aligned} f'_2(x_1, x_2) & = & 40 \cdot \frac{1}{x_2} \end{aligned}\]
2.Schritt: Einsetzen von \(\mathbf{a} = \left( \begin{array}{c} 5 \\ 3 \end{array} \right)\) in die partielle Ableitung \[\begin{aligned} f'_2(5, 3) & = & \frac{40}{3} = 13.333333 \end{aligned}\]
Bestimmen Sie die partielle Ableitung \(f'_1(x_1,x_2)\) der Funktion \[\begin{aligned} f(x_1, x_2) = -50 \cdot \ln \left (x_1 \right ) -20 \cdot \ln \left (x_2 \right ) \end{aligned}\] an der Stelle \(\mathbf{a} = \left( \begin{array}{c} 5 \\ 5.5 \end{array} \right)\).
1. Schritt: Ermittlung der partiellen Ableitung \[\begin{aligned} f'_1(x_1, x_2) & = & -50 \cdot \frac{1}{x_1} \end{aligned}\]
2.Schritt: Einsetzen von \(\mathbf{a} = \left( \begin{array}{c} 5 \\ 5.5 \end{array} \right)\) in die partielle Ableitung \[\begin{aligned} f'_1(5, 5.5) & = & \frac{-50}{5} = -10 \end{aligned}\]
Ein Unternehmen stellt ein Gut aus zwei Rohstoffen \(A\) und \(B\) her. Die herstellbare Menge des Gutes hängt ab von den Mengen an eingesetzten Rohstoffen gemäß der Produktionsfunktion \[\begin{aligned} q = f(x_1, x_2) = 9 x_1^{0.79} x_2^{0.08}. \end{aligned}\] Dabei bezeichnen \(x_1\) und \(x_2\) die eingesetzten Mengen der Rohstoffe \(A\) und \(B\) und \({q = f(x_1, x_2)}\) die hergestellte Menge des Produkts. Zurzeit stehen \(5\) Tonnen des Rohstoffs \(A\) und \(11\) Tonnen des Rohstoffs \(B\) zur Verfügung. Es besteht die Möglichkeit, die Zulieferung des Rohstoffs \(A\) um \(0.2\) Tonnen zu steigern, während die Zulieferungen des Rohstoffes \(B\) in Zukunft um \(0.2\) Tonnen sinken werden.
Wie wird sich die marginale Produktion durch die veränderten Zulieferungen verändern?
1. Schritt: Ermittlung der partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(x_1,x_2) = 9\cdot0.79x_1^{-0.21}x_2^{0.08}\\ f'_2(x_1,x_2) = 9\cdot0.08x_1^{0.79}x_2^{-0.92} \end{aligned}\]
2.Schritt: Einsetzen der verfügbaren Mengen \(x_1\), \(x_2\) von \(A\) und \(B\) in die partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(5,11) &=& 9\cdot0.79\cdot5^{-0.21}\cdot11^{0.08} = 6.143238 \\ f'_2(5,11) &=& 9\cdot0.08\cdot5^{0.79}\cdot11^{-0.92} = 0.282773 \end{aligned}\]
3. Schritt: Berechnung der momentanen marginalen Änderung der Produktion durch das totale Differential \[\begin{aligned} \text{d} q = \text{d} f(x_1, x_2) &=& \frac{\partial f}{\partial x_1} \text{d} x_1 + \frac{\partial f}{\partial x_2} \text{d} x_2 \\ &=& 6.143238 \cdot 0.2 + 0.282773 \cdot (- 0.2) \\ & = & 1.172093 \approx 1.17 \end{aligned}\]
Ein Unternehmen stellt ein Gut aus zwei Rohstoffen \(A\) und \(B\) her. Die herstellbare Menge des Gutes hängt ab von den Mengen an eingesetzten Rohstoffen gemäß der Produktionsfunktion \[\begin{aligned} q = f(x_1, x_2) = 9 x_1^{0.79} x_2^{0.09}. \end{aligned}\] Dabei bezeichnen \(x_1\) und \(x_2\) die eingesetzten Mengen der Rohstoffe \(A\) und \(B\) und \({q = f(x_1, x_2)}\) die hergestellte Menge des Produkts. Zurzeit stehen \(11\) Tonnen des Rohstoffs \(A\) und \(20\) Tonnen des Rohstoffs \(B\) zur Verfügung. Es besteht die Möglichkeit, die Zulieferung des Rohstoffs \(A\) um \(0.4\) Tonnen zu steigern, während die Zulieferungen des Rohstoffes \(B\) in Zukunft um \(0.1\) Tonnen sinken werden.
Wie wird sich die marginale Produktion durch die veränderten Zulieferungen verändern?
1. Schritt: Ermittlung der partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(x_1,x_2) = 9\cdot0.79x_1^{-0.21}x_2^{0.09}\\ f'_2(x_1,x_2) = 9\cdot0.09x_1^{0.79}x_2^{-0.91} \end{aligned}\]
2.Schritt: Einsetzen der verfügbaren Mengen \(x_1\), \(x_2\) von \(A\) und \(B\) in die partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(11,20) &=& 9\cdot0.79\cdot11^{-0.21}\cdot20^{0.09} = 5.626908 \\ f'_2(11,20) &=& 9\cdot0.09\cdot11^{0.79}\cdot20^{-0.91} = 0.352572 \end{aligned}\]
3. Schritt: Berechnung der momentanen marginalen Änderung der Produktion durch das totale Differential \[\begin{aligned} \text{d} q = \text{d} f(x_1, x_2) &=& \frac{\partial f}{\partial x_1} \text{d} x_1 + \frac{\partial f}{\partial x_2} \text{d} x_2 \\ &=& 5.626908 \cdot 0.4 + 0.352572 \cdot (- 0.1) \\ & = & 2.215506 \approx 2.22 \end{aligned}\]
Ein Unternehmen stellt ein Gut aus zwei Rohstoffen \(A\) und \(B\) her. Die herstellbare Menge des Gutes hängt ab von den Mengen an eingesetzten Rohstoffen gemäß der Produktionsfunktion \[\begin{aligned} q = f(x_1, x_2) = 9 x_1^{0.8} x_2^{0.07}. \end{aligned}\] Dabei bezeichnen \(x_1\) und \(x_2\) die eingesetzten Mengen der Rohstoffe \(A\) und \(B\) und \({q = f(x_1, x_2)}\) die hergestellte Menge des Produkts. Zurzeit stehen \(2\) Tonnen des Rohstoffs \(A\) und \(3\) Tonnen des Rohstoffs \(B\) zur Verfügung. Es besteht die Möglichkeit, die Zulieferung des Rohstoffs \(A\) um \(0.1\) Tonnen zu steigern, während die Zulieferungen des Rohstoffes \(B\) in Zukunft um \(0.5\) Tonnen sinken werden.
Wie wird sich die marginale Produktion durch die veränderten Zulieferungen verändern?
1. Schritt: Ermittlung der partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(x_1,x_2) = 9\cdot0.8x_1^{-0.2}x_2^{0.07}\\ f'_2(x_1,x_2) = 9\cdot0.07x_1^{0.8}x_2^{-0.93} \end{aligned}\]
2.Schritt: Einsetzen der verfügbaren Mengen \(x_1\), \(x_2\) von \(A\) und \(B\) in die partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(2,3) &=& 9\cdot0.8\cdot2^{-0.2}\cdot3^{0.07} = 6.769007 \\ f'_2(2,3) &=& 9\cdot0.07\cdot2^{0.8}\cdot3^{-0.93} = 0.394859 \end{aligned}\]
3. Schritt: Berechnung der momentanen marginalen Änderung der Produktion durch das totale Differential \[\begin{aligned} \text{d} q = \text{d} f(x_1, x_2) &=& \frac{\partial f}{\partial x_1} \text{d} x_1 + \frac{\partial f}{\partial x_2} \text{d} x_2 \\ &=& 6.769007 \cdot 0.1 + 0.394859 \cdot (- 0.5) \\ & = & 0.479471 \approx 0.48 \end{aligned}\]
Ein Unternehmen stellt ein Gut aus zwei Rohstoffen \(A\) und \(B\) her. Die herstellbare Menge des Gutes hängt ab von den Mengen an eingesetzten Rohstoffen gemäß der Produktionsfunktion \[\begin{aligned} q = f(x_1, x_2) = e^{0.45 x_1 + 0.3 x_2 + 0.4 x_1 x_2}. \end{aligned}\] Dabei bezeichnen \(x_1\) und \(x_2\) die eingesetzten Mengen der Rohstoffe \(A\) und \(B\) und \({q = f(x_1, x_2)}\) die hergestellte Menge des Produkts. Zurzeit stehen \(2.6\) Tonnen des Rohstoffs \(A\) und \(2.4\) Tonnen des Rohstoffs \(B\) zur Verfügung. Es besteht die Möglichkeit, die Zulieferung des Rohstoffs \(A\) um \(0.7\) Tonnen zu steigern, während die Zulieferungen des Rohstoffes \(B\) in Zukunft um \(1.8\) Tonnen sinken werden.
Wie wird sich die marginale Produktion durch die veränderten Zulieferungen verändern?
1. Schritt: Ermittlung der partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(x_1, x_2) &=& e^{0.45 x_1 + 0.3 x_2 + 0.4 x_1 x_2} \cdot \left( 0.45 + 0.4 x_2 \right) \\ f'_2(x_1, x_2) &=& e^{0.45 x_1 + 0.3 x_2 + 0.4 x_1 x_2} \cdot \left( 0.3 + 0.4 x_1 \right) \end{aligned}\]
2.Schritt: Einsetzen der verfügbaren Mengen \(x_1\), \(x_2\) von \(A\) und \(B\) in die partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(2.6,2.4) &=& e^{0.45 \cdot 2.6 + 0.3 \cdot 2.4 + 0.4 \cdot 2.6 \cdot 2.4} \cdot \left( 0.45 + 0.4 \cdot 2.4 \right) = 113.249087 \\ f'_2(2.6,2.4) &=& e^{0.45 \cdot 2.6 + 0.3 \cdot 2.4 + 0.4 \cdot 2.6 \cdot 2.4} \cdot \left( 0.3 + 0.4 \cdot 2.6 \right) = 107.626792 \end{aligned}\]
3. Schritt: Berechnung der momentanen marginalen Änderung der Produktion durch das totale Differential \[\begin{aligned} \text{d} q = \text{d} f(x_1, x_2) &=& \frac{\partial f}{\partial x_1} \text{d} x_1 + \frac{\partial f}{\partial x_2} \text{d} x_2 \\ &=& 113.249087 \cdot 0.7 + 107.626792 \cdot (- 1.8) \\ & = & -114.453865 \approx -114.45 \end{aligned}\]
Ein Unternehmen stellt ein Gut aus zwei Rohstoffen \(A\) und \(B\) her. Die herstellbare Menge des Gutes hängt ab von den Mengen an eingesetzten Rohstoffen gemäß der Produktionsfunktion \[\begin{aligned} q = f(x_1, x_2) = e^{0.05 x_1 + 0.45 x_2 + 0.4 x_1 x_2}. \end{aligned}\] Dabei bezeichnen \(x_1\) und \(x_2\) die eingesetzten Mengen der Rohstoffe \(A\) und \(B\) und \({q = f(x_1, x_2)}\) die hergestellte Menge des Produkts. Zurzeit stehen \(2.1\) Tonnen des Rohstoffs \(A\) und \(1.4\) Tonnen des Rohstoffs \(B\) zur Verfügung. Es besteht die Möglichkeit, die Zulieferung des Rohstoffs \(A\) um \(1.3\) Tonnen zu steigern, während die Zulieferungen des Rohstoffes \(B\) in Zukunft um \(1.2\) Tonnen sinken werden.
Wie wird sich die marginale Produktion durch die veränderten Zulieferungen verändern?
1. Schritt: Ermittlung der partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(x_1, x_2) &=& e^{0.05 x_1 + 0.45 x_2 + 0.4 x_1 x_2} \cdot \left( 0.05 + 0.4 x_2 \right) \\ f'_2(x_1, x_2) &=& e^{0.05 x_1 + 0.45 x_2 + 0.4 x_1 x_2} \cdot \left( 0.45 + 0.4 x_1 \right) \end{aligned}\]
2.Schritt: Einsetzen der verfügbaren Mengen \(x_1\), \(x_2\) von \(A\) und \(B\) in die partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(2.1,1.4) &=& e^{0.05 \cdot 2.1 + 0.45 \cdot 1.4 + 0.4 \cdot 2.1 \cdot 1.4} \cdot \left( 0.05 + 0.4 \cdot 1.4 \right) = 4.123506 \\ f'_2(2.1,1.4) &=& e^{0.05 \cdot 2.1 + 0.45 \cdot 1.4 + 0.4 \cdot 2.1 \cdot 1.4} \cdot \left( 0.45 + 0.4 \cdot 2.1 \right) = 8.7202 \end{aligned}\]
3. Schritt: Berechnung der momentanen marginalen Änderung der Produktion durch das totale Differential \[\begin{aligned} \text{d} q = \text{d} f(x_1, x_2) &=& \frac{\partial f}{\partial x_1} \text{d} x_1 + \frac{\partial f}{\partial x_2} \text{d} x_2 \\ &=& 4.123506 \cdot 1.3 + 8.7202 \cdot (- 1.2) \\ & = & -5.103683 \approx -5.10 \end{aligned}\]
Ein Unternehmen stellt ein Gut aus zwei Rohstoffen \(A\) und \(B\) her. Die herstellbare Menge des Gutes hängt ab von den Mengen an eingesetzten Rohstoffen gemäß der Produktionsfunktion \[\begin{aligned} q = f(x_1, x_2) = e^{0.15 x_1 + 0.25 x_2 + 0.35 x_1 x_2}. \end{aligned}\] Dabei bezeichnen \(x_1\) und \(x_2\) die eingesetzten Mengen der Rohstoffe \(A\) und \(B\) und \({q = f(x_1, x_2)}\) die hergestellte Menge des Produkts. Zurzeit stehen \(1.7\) Tonnen des Rohstoffs \(A\) und \(1.3\) Tonnen des Rohstoffs \(B\) zur Verfügung. Es besteht die Möglichkeit, die Zulieferung des Rohstoffs \(A\) um \(1.5\) Tonnen zu steigern, während die Zulieferungen des Rohstoffes \(B\) in Zukunft um \(0.6\) Tonnen sinken werden.
Wie wird sich die marginale Produktion durch die veränderten Zulieferungen verändern?
1. Schritt: Ermittlung der partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(x_1, x_2) &=& e^{0.15 x_1 + 0.25 x_2 + 0.35 x_1 x_2} \cdot \left( 0.15 + 0.35 x_2 \right) \\ f'_2(x_1, x_2) &=& e^{0.15 x_1 + 0.25 x_2 + 0.35 x_1 x_2} \cdot \left( 0.25 + 0.35 x_1 \right) \end{aligned}\]
2.Schritt: Einsetzen der verfügbaren Mengen \(x_1\), \(x_2\) von \(A\) und \(B\) in die partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(1.7,1.3) &=& e^{0.15 \cdot 1.7 + 0.25 \cdot 1.3 + 0.35 \cdot 1.7 \cdot 1.3} \cdot \left( 0.15 + 0.35 \cdot 1.3 \right) = 2.341925 \\ f'_2(1.7,1.3) &=& e^{0.15 \cdot 1.7 + 0.25 \cdot 1.3 + 0.35 \cdot 1.7 \cdot 1.3} \cdot \left( 0.25 + 0.35 \cdot 1.7 \right) = 3.270953 \end{aligned}\]
3. Schritt: Berechnung der momentanen marginalen Änderung der Produktion durch das totale Differential \[\begin{aligned} \text{d} q = \text{d} f(x_1, x_2) &=& \frac{\partial f}{\partial x_1} \text{d} x_1 + \frac{\partial f}{\partial x_2} \text{d} x_2 \\ &=& 2.341925 \cdot 1.5 + 3.270953 \cdot (- 0.6) \\ & = & 1.550316 \approx 1.55 \end{aligned}\]
Gegeben sei die Funktion \[\begin{aligned} f(x_1, x_2) = 25 \cdot \ln \left (x_1 \right ) + 10 \cdot \ln \left (x_2 \right ). \end{aligned}\] Wie stark ändert sich die Funktion an der Stelle \(a = (5, 5.5)\), wenn das erste Argument um \(0.3\) steigt und das zweite Argument um \(0.15\) sinkt? Berechnen Sie die dadurch hervorgerufene Funktionsänderung mit Hilfe des totalen Differentials.
1. Schritt: Ermittlung der partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(x_1, x_2) &=& 25 \cdot \frac{1}{x_1} \\ f'_2(x_1, x_2) &=& 10 \cdot \frac{1}{x_2} \end{aligned}\]
2.Schritt: Einsetzen des Punktes \(a = (5, 5.5)\) in die partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(5,5.5) &=& \frac{25}{5} = 5 \\ f'_2(5,5.5) &=& \frac{10}{5.5} = 1.818182 \end{aligned}\]
3. Schritt: Berechnung der momentanen marginalen Änderung der Funktion durch das totale Differential \[\begin{aligned} \text{d} f(x_1, x_2) &=& \frac{\partial f}{\partial x_1} \text{d} x_1 + \frac{\partial f}{\partial x_2} \text{d} x_2 \\ &=& 5 \cdot 0.3 + 1.818182 \cdot (- 0.15) \\ & = & 1.227273 \approx 1.23 \end{aligned}\]
Gegeben sei die Funktion \[\begin{aligned} f(x_1, x_2) = 36 \cdot \ln \left (x_1 \right ) + 27 \cdot \ln \left (x_2 \right ). \end{aligned}\] Wie stark ändert sich die Funktion an der Stelle \(a = (2, 2)\), wenn das erste Argument um \(0.25\) steigt und das zweite Argument um \(0.5\) sinkt? Berechnen Sie die dadurch hervorgerufene Funktionsänderung mit Hilfe des totalen Differentials.
1. Schritt: Ermittlung der partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(x_1, x_2) &=& 36 \cdot \frac{1}{x_1} \\ f'_2(x_1, x_2) &=& 27 \cdot \frac{1}{x_2} \end{aligned}\]
2.Schritt: Einsetzen des Punktes \(a = (2, 2)\) in die partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(2,2) &=& \frac{36}{2} = 18 \\ f'_2(2,2) &=& \frac{27}{2} = 13.5 \end{aligned}\]
3. Schritt: Berechnung der momentanen marginalen Änderung der Funktion durch das totale Differential \[\begin{aligned} \text{d} f(x_1, x_2) &=& \frac{\partial f}{\partial x_1} \text{d} x_1 + \frac{\partial f}{\partial x_2} \text{d} x_2 \\ &=& 18 \cdot 0.25 + 13.5 \cdot (- 0.5) \\ & = & -2.25 \approx -2.25 \end{aligned}\]
Gegeben sei die Funktion \[\begin{aligned} f(x_1, x_2) = 20 \cdot \ln \left (x_1 \right ) + 20 \cdot \ln \left (x_2 \right ). \end{aligned}\] Wie stark ändert sich die Funktion an der Stelle \(a = (2.5, 2.5)\), wenn das erste Argument um \(0.1\) steigt und das zweite Argument um \(0.15\) sinkt? Berechnen Sie die dadurch hervorgerufene Funktionsänderung mit Hilfe des totalen Differentials.
1. Schritt: Ermittlung der partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(x_1, x_2) &=& 20 \cdot \frac{1}{x_1} \\ f'_2(x_1, x_2) &=& 20 \cdot \frac{1}{x_2} \end{aligned}\]
2.Schritt: Einsetzen des Punktes \(a = (2.5, 2.5)\) in die partiellen Ableitungen \(f'_1(x_1,x_2)\) und \(f'_2(x_1,x_2)\) \[\begin{aligned} f'_1(2.5,2.5) &=& \frac{20}{2.5} = 8 \\ f'_2(2.5,2.5) &=& \frac{20}{2.5} = 8 \end{aligned}\]
3. Schritt: Berechnung der momentanen marginalen Änderung der Funktion durch das totale Differential \[\begin{aligned} \text{d} f(x_1, x_2) &=& \frac{\partial f}{\partial x_1} \text{d} x_1 + \frac{\partial f}{\partial x_2} \text{d} x_2 \\ &=& 8 \cdot 0.1 + 8 \cdot (- 0.15) \\ & = & -0.4 \approx -0.40 \end{aligned}\]
Ein Ackerbau wird mit \(x_1\) Einheiten Naturdünger und mit \(x_2\) Einheiten Kunstdünger behandelt. Die Ertragsfunktion lautet: \[\begin{aligned} E = f(x_1, x_2) = 3.5 x_1^{2} + 2 x_1 x_2 + 2.5 x_2^{2} \end{aligned}\] Der Düngemitteleinsatz von derzeit \(7\) Einheiten Naturdünger und \(19\) Einheiten Kunstdünger wird geändert, so dass \(2.3\)% weniger Naturdünger und \(2.4\)% mehr Kunstdünger eingesetzt werden.
Approximieren Sie die Änderung des Ertrags mit Hilfe des totalen Differentials.
1. Schritt: Ermittlung der partiellen Ableitungen \(f'_1(x_1, x_2)\) und \(f'_2(x_1, x_2)\): \[\begin{aligned} f'_1(x_1, x_2) & = & 2 \cdot 3.5 x_1 + 2 x_2 \\ f'_2(x_1, x_2) & = & 2 x_1 + 2 \cdot 2.5 x_2 \end{aligned}\]
2. Schritt: Einsetzen der verfügbaren Mengen für \(x_1\) und \(x_2\) von \(7\) und \(19\) Einheiten in die partiellen Ableitungen \(f'_1(x_1, x_2)\) und \(f'_2(x_1, x_2)\): \[\begin{aligned} f'_1(7, 19) & = & 2 \cdot 3.5 \cdot 7 + 2\cdot 19 = 87 \\ f'_2(7, 19) & = & 2 \cdot 7 + 2 \cdot 2.5 \cdot 19 = 109 \end{aligned}\]
3. Schritt: Approximation der Änderung des Ertrags durch das totale Differential, wenn der Einsatz von Naturdünger um \(\text{d} x_1 = 7 \cdot 0.023 = 0.161\) Einheiten sinkt und der Einsatz von Kunstdünger um \(\text{d} x_2 = 19 \cdot 0.024 = 0.456\) Einheiten steigt: \[\begin{aligned} \text{d} E & = & \text{d} f(x_1, x_2) \\ & = & \frac{\partial f}{\partial x_1} \cdot \text{d} x_1 + \frac{\partial f}{\partial x_2} \cdot \text{d} x_2 \\ & = & 87 \cdot ( - 0.161 ) + 109 \cdot 0.456 \\ & \approx & 35.70 \end{aligned}\] Der Ertrag steigt somit approximativ um \(35.70\) Einheiten.
Ein Ackerbau wird mit \(x_1\) Einheiten Naturdünger und mit \(x_2\) Einheiten Kunstdünger behandelt. Die Ertragsfunktion lautet: \[\begin{aligned} E = f(x_1, x_2) = 6 x_1^{2} + 3.5 x_1 x_2 + 6 x_2^{2} \end{aligned}\] Der Düngemitteleinsatz von derzeit \(6\) Einheiten Naturdünger und \(5\) Einheiten Kunstdünger wird geändert, so dass \(2\)% weniger Naturdünger und \(3.4\)% mehr Kunstdünger eingesetzt werden.
Approximieren Sie die Änderung des Ertrags mit Hilfe des totalen Differentials.
1. Schritt: Ermittlung der partiellen Ableitungen \(f'_1(x_1, x_2)\) und \(f'_2(x_1, x_2)\): \[\begin{aligned} f'_1(x_1, x_2) & = & 2 \cdot 6 x_1 + 3.5 x_2 \\ f'_2(x_1, x_2) & = & 3.5 x_1 + 2 \cdot 6 x_2 \end{aligned}\]
2. Schritt: Einsetzen der verfügbaren Mengen für \(x_1\) und \(x_2\) von \(6\) und \(5\) Einheiten in die partiellen Ableitungen \(f'_1(x_1, x_2)\) und \(f'_2(x_1, x_2)\): \[\begin{aligned} f'_1(6, 5) & = & 2 \cdot 6 \cdot 6 + 3.5\cdot 5 = 89.5 \\ f'_2(6, 5) & = & 3.5 \cdot 6 + 2 \cdot 6 \cdot 5 = 81 \end{aligned}\]
3. Schritt: Approximation der Änderung des Ertrags durch das totale Differential, wenn der Einsatz von Naturdünger um \(\text{d} x_1 = 6 \cdot 0.02 = 0.12\) Einheiten sinkt und der Einsatz von Kunstdünger um \(\text{d} x_2 = 5 \cdot 0.034 = 0.17\) Einheiten steigt: \[\begin{aligned} \text{d} E & = & \text{d} f(x_1, x_2) \\ & = & \frac{\partial f}{\partial x_1} \cdot \text{d} x_1 + \frac{\partial f}{\partial x_2} \cdot \text{d} x_2 \\ & = & 89.5 \cdot ( - 0.12 ) + 81 \cdot 0.17 \\ & \approx & 3.03 \end{aligned}\] Der Ertrag steigt somit approximativ um \(3.03\) Einheiten.
Ein Ackerbau wird mit \(x_1\) Einheiten Naturdünger und mit \(x_2\) Einheiten Kunstdünger behandelt. Die Ertragsfunktion lautet: \[\begin{aligned} E = f(x_1, x_2) = 3.5 x_1^{2} + 6 x_1 x_2 + 2.5 x_2^{2} \end{aligned}\] Der Düngemitteleinsatz von derzeit \(12\) Einheiten Naturdünger und \(13\) Einheiten Kunstdünger wird geändert, so dass \(1.3\)% weniger Naturdünger und \(4.6\)% mehr Kunstdünger eingesetzt werden.
Approximieren Sie die Änderung des Ertrags mit Hilfe des totalen Differentials.
1. Schritt: Ermittlung der partiellen Ableitungen \(f'_1(x_1, x_2)\) und \(f'_2(x_1, x_2)\): \[\begin{aligned} f'_1(x_1, x_2) & = & 2 \cdot 3.5 x_1 + 6 x_2 \\ f'_2(x_1, x_2) & = & 6 x_1 + 2 \cdot 2.5 x_2 \end{aligned}\]
2. Schritt: Einsetzen der verfügbaren Mengen für \(x_1\) und \(x_2\) von \(12\) und \(13\) Einheiten in die partiellen Ableitungen \(f'_1(x_1, x_2)\) und \(f'_2(x_1, x_2)\): \[\begin{aligned} f'_1(12, 13) & = & 2 \cdot 3.5 \cdot 12 + 6\cdot 13 = 162 \\ f'_2(12, 13) & = & 6 \cdot 12 + 2 \cdot 2.5 \cdot 13 = 137 \end{aligned}\]
3. Schritt: Approximation der Änderung des Ertrags durch das totale Differential, wenn der Einsatz von Naturdünger um \(\text{d} x_1 = 12 \cdot 0.013 = 0.156\) Einheiten sinkt und der Einsatz von Kunstdünger um \(\text{d} x_2 = 13 \cdot 0.046 = 0.598\) Einheiten steigt: \[\begin{aligned} \text{d} E & = & \text{d} f(x_1, x_2) \\ & = & \frac{\partial f}{\partial x_1} \cdot \text{d} x_1 + \frac{\partial f}{\partial x_2} \cdot \text{d} x_2 \\ & = & 162 \cdot ( - 0.156 ) + 137 \cdot 0.598 \\ & \approx & 56.65 \end{aligned}\] Der Ertrag steigt somit approximativ um \(56.65\) Einheiten.
Partielle Ableitungen zweiter Ordnung
Bestimmen Sie die Hesse-Matrix \(\mathbf{A}\) der Funktion \[\begin{aligned} f(x_1, x_2) = 111 x_1^{0.6} x_2^{0.3} \end{aligned}\] an der Stelle \(\left( \begin{array}{c} 9.4 \\ 8.3 \end{array} \right)\).
Welchen Wert hat \(\det \mathbf{A}\)?
Die partiellen Ableitungen erster Ordnung sind \[\begin{aligned} f'_1(x_1, x_2) & = & 66.6 x_1^{-0.4} x_2^{0.3},\\ f'_2(x_1, x_2) & = & 33.3 x_1^{0.6} x_2^{-0.7}. \end{aligned}\] Die partiellen Ableitungen zweiter Ordnung sind \[\begin{aligned} f''_{11}(x_1, x_2) & = & -26.64 x_1^{-1.4} x_2^{0.3}\\ f''_{12}(x_1, x_2) & = & 19.98 x_1^{-0.4} x_2^{-0.7}\\ f''_{21}(x_1, x_2) & = & 19.98 x_1^{-0.4} x_2^{-0.7}\\ f''_{22}(x_1, x_2) & = & -23.31 x_1^{0.6} x_2^{-1.7} \end{aligned}\] Einsetzen von \(\left( \begin{array}{c} 9.4 \\ 8.3 \end{array} \right)\) in die partiellen Ableitungen zweiter Ordnung: \[\begin{aligned} f''_{11}(9.4, 8.3) & = & -2.18212\\ f''_{12}(9.4, 8.3) & = & 1.853488\\ f''_{21}(9.4, 8.3) & = & 1.853488\\ f''_{22}(9.4, 8.3) & = & -2.448986 \end{aligned}\] Die Hesse-Matrix \(\mathbf{A}\) der gegebenen Funktion \(f(x_1, x_2) = 111 x_1^{0.6} x_2^{0.3}\) an der Stelle \(\left( \begin{array}{c} 9.4 \\ 8.3 \end{array} \right)\) lautet damit \[\begin{aligned} \mathbf{A} = f''(9.4, 8.3) & = & \left( \begin{array}{rr} -2.18212 & 1.853488\\ 1.853488 & -2.448986 \end{array} \right). \end{aligned}\] Die Determinante von \(\mathbf{A}\) ist dann \[\begin{aligned} \det \mathbf{A} & = & -2.18212 \cdot (-2.448986) - 1.853488 \cdot 1.853488 \\ & = & 1.908565 \approx 1.91 \end{aligned}\]
Bestimmen Sie die Hesse-Matrix \(\mathbf{A}\) der Funktion \[\begin{aligned} f(x_1, x_2) = 166 x_1^{0.5} x_2^{0.4} \end{aligned}\] an der Stelle \(\left( \begin{array}{c} 9.8 \\ 9 \end{array} \right)\).
Welchen Wert hat \(\det \mathbf{A}\)?
Die partiellen Ableitungen erster Ordnung sind \[\begin{aligned} f'_1(x_1, x_2) & = & 83 x_1^{-0.5} x_2^{0.4},\\ f'_2(x_1, x_2) & = & 66.4 x_1^{0.5} x_2^{-0.6}. \end{aligned}\] Die partiellen Ableitungen zweiter Ordnung sind \[\begin{aligned} f''_{11}(x_1, x_2) & = & -41.5 x_1^{-1.5} x_2^{0.4}\\ f''_{12}(x_1, x_2) & = & 33.2 x_1^{-0.5} x_2^{-0.6}\\ f''_{21}(x_1, x_2) & = & 33.2 x_1^{-0.5} x_2^{-0.6}\\ f''_{22}(x_1, x_2) & = & -39.84 x_1^{0.5} x_2^{-1.6} \end{aligned}\] Einsetzen von \(\left( \begin{array}{c} 9.8 \\ 9 \end{array} \right)\) in die partiellen Ableitungen zweiter Ordnung: \[\begin{aligned} f''_{11}(9.8, 9) & = & -3.257662\\ f''_{12}(9.8, 9) & = & 2.837785\\ f''_{21}(9.8, 9) & = & 2.837785\\ f''_{22}(9.8, 9) & = & -3.70804 \end{aligned}\] Die Hesse-Matrix \(\mathbf{A}\) der gegebenen Funktion \(f(x_1, x_2) = 166 x_1^{0.5} x_2^{0.4}\) an der Stelle \(\left( \begin{array}{c} 9.8 \\ 9 \end{array} \right)\) lautet damit \[\begin{aligned} \mathbf{A} = f''(9.8, 9) & = & \left( \begin{array}{rr} -3.257662 & 2.837785\\ 2.837785 & -3.70804 \end{array} \right). \end{aligned}\] Die Determinante von \(\mathbf{A}\) ist dann \[\begin{aligned} \det \mathbf{A} & = & -3.257662 \cdot (-3.70804) - 2.837785 \cdot 2.837785 \\ & = & 4.026513 \approx 4.03 \end{aligned}\]
Bestimmen Sie die Hesse-Matrix \(\mathbf{A}\) der Funktion \[\begin{aligned} f(x_1, x_2) = 77 x_1^{0.59} x_2^{0.31} \end{aligned}\] an der Stelle \(\left( \begin{array}{c} 7.1 \\ 5.9 \end{array} \right)\).
Welchen Wert hat \(\det \mathbf{A}\)?
Die partiellen Ableitungen erster Ordnung sind \[\begin{aligned} f'_1(x_1, x_2) & = & 45.43 x_1^{-0.41} x_2^{0.31},\\ f'_2(x_1, x_2) & = & 23.87 x_1^{0.59} x_2^{-0.69}. \end{aligned}\] Die partiellen Ableitungen zweiter Ordnung sind \[\begin{aligned} f''_{11}(x_1, x_2) & = & -18.6263 x_1^{-1.41} x_2^{0.31}\\ f''_{12}(x_1, x_2) & = & 14.0833 x_1^{-0.41} x_2^{-0.69}\\ f''_{21}(x_1, x_2) & = & 14.0833 x_1^{-0.41} x_2^{-0.69}\\ f''_{22}(x_1, x_2) & = & -16.4703 x_1^{0.59} x_2^{-1.69} \end{aligned}\] Einsetzen von \(\left( \begin{array}{c} 7.1 \\ 5.9 \end{array} \right)\) in die partiellen Ableitungen zweiter Ordnung: \[\begin{aligned} f''_{11}(7.1, 5.9) & = & -2.036181\\ f''_{12}(7.1, 5.9) & = & 1.852681\\ f''_{21}(7.1, 5.9) & = & 1.852681\\ f''_{22}(7.1, 5.9) & = & -2.607378 \end{aligned}\] Die Hesse-Matrix \(\mathbf{A}\) der gegebenen Funktion \(f(x_1, x_2) = 77 x_1^{0.59} x_2^{0.31}\) an der Stelle \(\left( \begin{array}{c} 7.1 \\ 5.9 \end{array} \right)\) lautet damit \[\begin{aligned} \mathbf{A} = f''(7.1, 5.9) & = & \left( \begin{array}{rr} -2.036181 & 1.852681\\ 1.852681 & -2.607378 \end{array} \right). \end{aligned}\] Die Determinante von \(\mathbf{A}\) ist dann \[\begin{aligned} \det \mathbf{A} & = & -2.036181 \cdot (-2.607378) - 1.852681 \cdot 1.852681 \\ & = & 1.876668 \approx 1.88 \end{aligned}\]
Bestimmen Sie die Hesse-Matrix der Funktion \[\begin{aligned} f(x_1, x_2) = e^{5 x_1 -5 x_2 + 4 x_1 x_2} \end{aligned}\] an der Stelle \((x_1, x_2) = (-0.54, -0.74)\). Welchen Wert hat der Eintrag rechts oben?
Die partiellen Ableitungen erster Ordnung sind \[\begin{aligned} f'_1(x_1, x_2) &=& (5 + 4 x_2) \cdot e^{5 x_1 -5 x_2 + 4 x_1 x_2}, \\ f'_2(x_1, x_2) &=& (-5 + 4 x_1) \cdot e^{5 x_1 -5 x_2 + 4 x_1 x_2}. \end{aligned}\] Die partiellen Ableitungen zweiter Ordnung sind \[\begin{aligned} f''_{11}(x_1, x_2) &=& (5 + 4 x_2)^2 \cdot e^{5 x_1 -5 x_2 + 4 x_1 x_2},\\ f''_{12}(x_1, x_2) &=& (4 + (5 + 4 x_2) \cdot (-5 + 4 x_1)) \cdot e^{5 x_1 -5 x_2 + 4 x_1 x_2}\\ &=& (-21 + 20 x_1 -20 x_2 + 16 x_1 x_2) \cdot e^{5 x_1 -5 x_2 + 4 x_1 x_2},\\ f''_{21}(x_1, x_2) &=& (4 + (-5 + 4 x_1) \cdot (5 + 4 x_2)) \cdot e^{5 x_1 -5 x_2 + 4 x_1 x_2}\\ &=& (-21 + 20 x_1 -20 x_2 + 16 x_1 x_2) \cdot e^{5 x_1 -5 x_2 + 4 x_1 x_2},\\ f''_{22}(x_1, x_2) &=& (-5 + 4 x_1)^2 \cdot e^{5 x_1 -5 x_2 + 4 x_1 x_2}. \end{aligned}\]
Somit gilt \[\begin{aligned} f''(-0.54, -0.74) = \left( \begin{array}{rr} 55.941115 & -142.573491 \\ -142.573491 & 689.123129 \end{array} \right). \end{aligned}\] Der Eintrag der Hesse-Matrix rechts oben hat damit den Wert: \(f''_{12}(-0.54, -0.74) = -142.57\)
Bestimmen Sie die Hesse-Matrix der Funktion \[\begin{aligned} f(x_1, x_2) = e^{-3 x_1 -4 x_2 -2 x_1 x_2} \end{aligned}\] an der Stelle \((x_1, x_2) = (0.42, -0.43)\). Welchen Wert hat der Eintrag rechts oben?
Die partiellen Ableitungen erster Ordnung sind \[\begin{aligned} f'_1(x_1, x_2) &=& (-3 -2 x_2) \cdot e^{-3 x_1 -4 x_2 -2 x_1 x_2}, \\ f'_2(x_1, x_2) &=& (-4 -2 x_1) \cdot e^{-3 x_1 -4 x_2 -2 x_1 x_2}. \end{aligned}\] Die partiellen Ableitungen zweiter Ordnung sind \[\begin{aligned} f''_{11}(x_1, x_2) &=& (-3 -2 x_2)^2 \cdot e^{-3 x_1 -4 x_2 -2 x_1 x_2},\\ f''_{12}(x_1, x_2) &=& (-2 + (-3 -2 x_2) \cdot (-4 -2 x_1)) \cdot e^{-3 x_1 -4 x_2 -2 x_1 x_2}\\ &=& (10 + 6 x_1 + 8 x_2 + 4 x_1 x_2) \cdot e^{-3 x_1 -4 x_2 -2 x_1 x_2},\\ f''_{21}(x_1, x_2) &=& (-2 + (-4 -2 x_1) \cdot (-3 -2 x_2)) \cdot e^{-3 x_1 -4 x_2 -2 x_1 x_2}\\ &=& (10 + 6 x_1 + 8 x_2 + 4 x_1 x_2) \cdot e^{-3 x_1 -4 x_2 -2 x_1 x_2},\\ f''_{22}(x_1, x_2) &=& (-4 -2 x_1)^2 \cdot e^{-3 x_1 -4 x_2 -2 x_1 x_2}. \end{aligned}\]
Somit gilt \[\begin{aligned} f''(0.42, -0.43) = \left( \begin{array}{rr} 10.410466 & 18.998714 \\ 18.998714 & 53.251685 \end{array} \right). \end{aligned}\] Der Eintrag der Hesse-Matrix rechts oben hat damit den Wert: \(f''_{12}(0.42, -0.43) = 19.00\)
Bestimmen Sie die Hesse-Matrix der Funktion \[\begin{aligned} f(x_1, x_2) = e^{2 x_1 -2 x_2 + 5 x_1 x_2} \end{aligned}\] an der Stelle \((x_1, x_2) = (-0.67, -0.88)\). Welchen Wert hat der Eintrag rechts oben?
Die partiellen Ableitungen erster Ordnung sind \[\begin{aligned} f'_1(x_1, x_2) &=& (2 + 5 x_2) \cdot e^{2 x_1 -2 x_2 + 5 x_1 x_2}, \\ f'_2(x_1, x_2) &=& (-2 + 5 x_1) \cdot e^{2 x_1 -2 x_2 + 5 x_1 x_2}. \end{aligned}\] Die partiellen Ableitungen zweiter Ordnung sind \[\begin{aligned} f''_{11}(x_1, x_2) &=& (2 + 5 x_2)^2 \cdot e^{2 x_1 -2 x_2 + 5 x_1 x_2},\\ f''_{12}(x_1, x_2) &=& (5 + (2 + 5 x_2) \cdot (-2 + 5 x_1)) \cdot e^{2 x_1 -2 x_2 + 5 x_1 x_2}\\ &=& (1 + 10 x_1 -10 x_2 + 25 x_1 x_2) \cdot e^{2 x_1 -2 x_2 + 5 x_1 x_2},\\ f''_{21}(x_1, x_2) &=& (5 + (-2 + 5 x_1) \cdot (2 + 5 x_2)) \cdot e^{2 x_1 -2 x_2 + 5 x_1 x_2}\\ &=& (1 + 10 x_1 -10 x_2 + 25 x_1 x_2) \cdot e^{2 x_1 -2 x_2 + 5 x_1 x_2},\\ f''_{22}(x_1, x_2) &=& (-2 + 5 x_1)^2 \cdot e^{2 x_1 -2 x_2 + 5 x_1 x_2}. \end{aligned}\]
Somit gilt \[\begin{aligned} f''(-0.67, -0.88) = \left( \begin{array}{rr} 167.157666 & 517.724438 \\ 517.724438 & 830.637204 \end{array} \right). \end{aligned}\] Der Eintrag der Hesse-Matrix rechts oben hat damit den Wert: \(f''_{12}(-0.67, -0.88) = 517.72\)
Globale Optimierung
Die Funktion \[\begin{aligned} f(x_1,x_2)= -3x_1^2 - 4x_1 x_2 - 2x_2^2 + 22x_1 + 20x_2 - 30 \end{aligned}\] besitzt ein globales Optimum an der Stelle \(\mathbf{a}\). Welchen Wert hat die Funktion an der Stelle \(\mathbf{a}\)?
Wir bilden zunächst die ersten partiellen Ableitungen und setzen diese Null: \[\begin{aligned} f'_1 &=& -6x_1 - 4x_2 + 22 = 0 \\ f'_2 &=& -4x_1 - 4x_2 + 20 = 0 \end{aligned}\] Die Lösung dieses Gleichungssystems \[\begin{aligned} x_1 &=& 1 \\ x_2 &=& 4 \end{aligned}\] liefert den kritischen Punkt \[\begin{aligned} \mathbf{a} = (1, 4)^\top. \end{aligned}\]
Im globalen Optimum hat die Funktion den Wert \[\begin{aligned} f(1,4) &=& -3 \cdot 1^2 - 4 \cdot 1 \cdot 4 - 2 \cdot 4^2 + 22 \cdot 1 + 20 \cdot 4 - 30 \\ &=& 21 \end{aligned}\]
Der Funktionswert im globalen Optimum \(\mathbf{a} = (1, 4)^\top\) beträgt \(21.00\).
Die Funktion \[\begin{aligned} f(x_1,x_2)= 5x_1^2 + 4x_1 x_2 + 4x_2^2 - 64x_1 - 64x_2 - 8 \end{aligned}\] besitzt ein globales Optimum an der Stelle \(\mathbf{a}\). Welchen Wert hat die Funktion an der Stelle \(\mathbf{a}\)?
Wir bilden zunächst die ersten partiellen Ableitungen und setzen diese Null: \[\begin{aligned} f'_1 &=& 10x_1 + 4x_2 - 64 = 0 \\ f'_2 &=& 4x_1 + 8x_2 - 64 = 0 \end{aligned}\] Die Lösung dieses Gleichungssystems \[\begin{aligned} x_1 &=& 4 \\ x_2 &=& 6 \end{aligned}\] liefert den kritischen Punkt \[\begin{aligned} \mathbf{a} = (4, 6)^\top. \end{aligned}\]
Im globalen Optimum hat die Funktion den Wert \[\begin{aligned} f(4,6) &=& 5 \cdot 4^2 + 4 \cdot 4 \cdot 6 + 4 \cdot 6^2 - 64 \cdot 4 - 64 \cdot 6 - 8 \\ &=& -328 \end{aligned}\]
Der Funktionswert im globalen Optimum \(\mathbf{a} = (4, 6)^\top\) beträgt \(-328.00\).
Die Funktion \[\begin{aligned} f(x_1,x_2)= 4x_1^2 - 2x_1 x_2 + 6x_2^2 + 2x_1 + 34x_2 - 12 \end{aligned}\] besitzt ein globales Optimum an der Stelle \(\mathbf{a}\). Welchen Wert hat die Funktion an der Stelle \(\mathbf{a}\)?
Wir bilden zunächst die ersten partiellen Ableitungen und setzen diese Null: \[\begin{aligned} f'_1 &=& 8x_1 - 2x_2 + 2 = 0 \\ f'_2 &=& -2x_1 + 12x_2 + 34 = 0 \end{aligned}\] Die Lösung dieses Gleichungssystems \[\begin{aligned} x_1 &=& -1 \\ x_2 &=& -3 \end{aligned}\] liefert den kritischen Punkt \[\begin{aligned} \mathbf{a} = (-1, -3)^\top. \end{aligned}\]
Im globalen Optimum hat die Funktion den Wert \[\begin{aligned} f(-1,-3) &=& 4 \cdot (-1)^2 - 2 \cdot (-1) \cdot (-3) + 6 \cdot (-3)^2 + 2 \cdot (-1) + 34 \cdot (-3) - 12 \\ &=& -64 \end{aligned}\]
Der Funktionswert im globalen Optimum \(\mathbf{a} = (-1, -3)^\top\) beträgt \(-64.00\).
Die Funktion \(f(x_1, x_2)\) ist in Abhängigkeit von den zwei Parametern \(b\) und \(d\) definiert als: \[\begin{aligned}
f(x_1,x_2)= -7x_1^2 + 4x_1 x_2 - 2x_2^2 + b x_1 + d x_2 + 8
\end{aligned}\] Bei geeigneter Wahl von \(b\) und \(d\) besitzt die Funktion ein globales Optimum an der Stelle \(\mathbf{x} = \left(\begin{array}{cc} 2 & -5 \end{array} \right) ^\top\).
Wie lautet der Parameter \(b\)?
Wir bilden zunächst die partiellen Ableitungen erster Ordnung und setzen diese Null: \[\begin{aligned}
f'_1 &=& -14x_1 + 4x_2 + b \stackrel{!}{=} 0 \\
f'_2 &=& 4x_1 - 4x_2 + d \stackrel{!}{=} 0
\end{aligned}\] Nun können wir \(x_1 = 2\) und \(x_2 = -5\) in das Gleichungssystem einsetzen und die beiden Parameter freistellen: \[\begin{aligned}
f'_1 &=& -14\cdot 2 + 4 \cdot (-5) + b \stackrel{!}{=} 0 \; \Rightarrow \; b = 48\\
f'_2 &=& 4 \cdot 2 - 4 \cdot (-5) + d \stackrel{!}{=} 0 \; \Rightarrow \; d = -28
\end{aligned}\] Um zu überprüfen, ob es sich tatsächlich um ein globales Optimum handelt, muss die Bedingung zweiter Ordnung erfüllt sein:
Dazu benötigen wir die Hesse-Matrix: \[\begin{aligned}
f''(x_1, x_2) = \mathbf{A} = \left( \begin{array}{rr} -14 & 4 \\ 4 & -4 \end{array} \right)
\end{aligned}\] Da \(a_{11} \leq 0\) und \(\det \mathbf{A} = 40.00 \geq 0\) handelt es sich um ein Maximum.
Damit die Funktion \(f(x_1, x_2)\) an der Stelle \(\mathbf{x} = \left(\begin{array}{cc} 2 & -5 \end{array} \right)^\top\) ein globales Optimum besitzt, müssen die Parameter \(b\) und \(d\) die Werte \(48\) und \(-28\) annehmen.
Der Parameter \(b\) muss \(48\) betragen.
Die Funktion \(f(x_1, x_2)\) ist in Abhängigkeit von den zwei Parametern \(b\) und \(d\) definiert als: \[\begin{aligned}
f(x_1,x_2)= 4x_1^2 + 4x_1 x_2 + 3x_2^2 + b x_1 + d x_2 - 27
\end{aligned}\] Bei geeigneter Wahl von \(b\) und \(d\) besitzt die Funktion ein globales Optimum an der Stelle \(\mathbf{x} = \left(\begin{array}{cc} -2 & 5 \end{array} \right) ^\top\).
Welchen Wert besitzt die Funktion in diesem Optimum?
Wir bilden zunächst die partiellen Ableitungen erster Ordnung und setzen diese Null: \[\begin{aligned}
f'_1 &=& 8x_1 + 4x_2 + b \stackrel{!}{=} 0 \\
f'_2 &=& 4x_1 + 6x_2 + d \stackrel{!}{=} 0
\end{aligned}\] Nun können wir \(x_1 = -2\) und \(x_2 = 5\) in das Gleichungssystem einsetzen und die beiden Parameter freistellen: \[\begin{aligned}
f'_1 &=& 8\cdot (-2) + 4 \cdot 5 + b \stackrel{!}{=} 0 \; \Rightarrow \; b = -4\\
f'_2 &=& 4 \cdot (-2) + 6 \cdot 5 + d \stackrel{!}{=} 0 \; \Rightarrow \; d = -22
\end{aligned}\] Um zu überprüfen, ob es sich tatsächlich um ein globales Optimum handelt, muss die Bedingung zweiter Ordnung erfüllt sein:
Dazu benötigen wir die Hesse-Matrix: \[\begin{aligned}
f''(x_1, x_2) = \mathbf{A} = \left( \begin{array}{rr} 8 & 4 \\ 4 & 6 \end{array} \right)
\end{aligned}\] Da \(a_{11} \geq 0\) und \(\det \mathbf{A} = 32.00 \geq 0\) handelt es sich um ein Minimum.
Damit die Funktion \(f(x_1, x_2)\) an der Stelle \(\mathbf{x} = \left(\begin{array}{cc} -2 & 5 \end{array} \right)^\top\) ein globales Optimum besitzt, müssen die Parameter \(b\) und \(d\) die Werte \(-4\) und \(-22\) annehmen.
Im globalen Optimum hat die Funktion den Wert \[\begin{aligned} f(-2,5) &=& 4 \cdot (-2)^2 + 4 \cdot (-2) \cdot 5 + 3 \cdot 5^2 - 4 \cdot (-2) - 22 \cdot 5 - 27 \\ &=& -78 \end{aligned}\]
Der Funktionswert im globalen Optimum \(f (-2, 5)\) beträgt \(-78.00\).
Die Funktion \(f(x_1, x_2)\) ist in Abhängigkeit von den zwei Parametern \(b\) und \(d\) definiert als: \[\begin{aligned}
f(x_1,x_2)= 3x_1^2 - 3x_1 x_2 + 4x_2^2 + b x_1 + d x_2 + 4
\end{aligned}\] Bei geeigneter Wahl von \(b\) und \(d\) besitzt die Funktion ein globales Optimum an der Stelle \(\mathbf{x} = \left(\begin{array}{cc} -3 & 1 \end{array} \right) ^\top\).
Welchen Wert besitzt die Funktion in diesem Optimum?
Wir bilden zunächst die partiellen Ableitungen erster Ordnung und setzen diese Null: \[\begin{aligned}
f'_1 &=& 6x_1 - 3x_2 + b \stackrel{!}{=} 0 \\
f'_2 &=& -3x_1 + 8x_2 + d \stackrel{!}{=} 0
\end{aligned}\] Nun können wir \(x_1 = -3\) und \(x_2 = 1\) in das Gleichungssystem einsetzen und die beiden Parameter freistellen: \[\begin{aligned}
f'_1 &=& 6\cdot (-3) - 3 \cdot 1 + b \stackrel{!}{=} 0 \; \Rightarrow \; b = 21\\
f'_2 &=& -3 \cdot (-3) + 8 \cdot 1 + d \stackrel{!}{=} 0 \; \Rightarrow \; d = -17
\end{aligned}\] Um zu überprüfen, ob es sich tatsächlich um ein globales Optimum handelt, muss die Bedingung zweiter Ordnung erfüllt sein:
Dazu benötigen wir die Hesse-Matrix: \[\begin{aligned}
f''(x_1, x_2) = \mathbf{A} = \left( \begin{array}{rr} 6 & -3 \\ -3 & 8 \end{array} \right)
\end{aligned}\] Da \(a_{11} \geq 0\) und \(\det \mathbf{A} = 39.00 \geq 0\) handelt es sich um ein Minimum.
Damit die Funktion \(f(x_1, x_2)\) an der Stelle \(\mathbf{x} = \left(\begin{array}{cc} -3 & 1 \end{array} \right)^\top\) ein globales Optimum besitzt, müssen die Parameter \(b\) und \(d\) die Werte \(21\) und \(-17\) annehmen.
Im globalen Optimum hat die Funktion den Wert \[\begin{aligned} f(-3,1) &=& 3 \cdot (-3)^2 - 3 \cdot (-3) \cdot 1 + 4 \cdot 1^2 + 21 \cdot (-3) - 17 \cdot 1 + 4 \\ &=& -36 \end{aligned}\]
Der Funktionswert im globalen Optimum \(f (-3, 1)\) beträgt \(-36.00\).
Ein Monopolunternehmen bietet zwei Güter \(A\) und \(B\) zu den (veränderbaren) Preisen \(p_1\) (Gut \(A\)) und \(p_2\) (Gut \(B\)) an. Die Nachfrage nach diesen beiden Gütern wird durch die beiden Nachfragefunktionen \[\begin{aligned} q_1(p_1,p_2) &=& 91 -23 p_{1}+ 14 p_{2}, \\ q_2(p_1,p_2) &=& 96 -6 p_{1} -7 p_{2} \end{aligned}\] bestimmt, wobei \(q_1\) die Nachfrage nach Gut \(A\) und \(q_2\) die Nachfrage nach Gut \(B\) beschreibt. Die Herstellungskosten für die beiden Güter betragen pro Stück \(4\) GE (Gut \(A\)) und \(2\) GE (Gut \(B\)). Es gibt ein eindeutig bestimmtes Paar \((p_1, p_2)\) von Preisen für die beiden Güter \(A\) und \(B\), sodass das Unternehmen maximalen Gewinn erzielt.
Wie groß ist die Verkaufsmenge \(q_{2}(p_1,p_2)\), wenn die Preise \(p_1\) und \(p_2\) so gewählt werden, dass maximaler Gewinn erzielt wird?
Für den erzielten Gewinn \(\pi\) in Abhängigkeit von den gewählten Preisen \(p_1\) und \(p_2\) erhalten wir \[\begin{aligned} \pi(p_1,p_2) &=& p_1 \cdot q_1(p_1,p_2) + p_2 \cdot q_2(p_1,p_2) - 4 \cdot q_1(p_1,p_2) - 2 \cdot q_2(p_1,p_2) = \\ &=& -556+ 195 p_{1}+ 54 p_{2} -23 p_{1}^{2} -7 p_{2}^{2}+ 8 p_{1} p_{2}. \end{aligned}\] Die partiellen Ableitungen von \(\pi\) sind \[\begin{aligned} \pi'_1(p_1,p_2) &=& 195 -46 p_{1}+ 8 p_{2}, \\ \pi'_2(p_1,p_2) &=& 54+ 8 p_{1} -14 p_{2}, \end{aligned}\] die Hesse-Matrix von \(\pi\) ist \[\begin{aligned} \pi''(p_1,p_2) = \left( \begin{array}{rr} -46 & 8 \\ 8 & -14 \end{array} \right). \end{aligned}\] Daraus erkennen wir, dass die Funktion \(\pi\) tatsächlich genau einen globalen Maximierer besitzt, denn das (lineare) Gleichungssystem \[\begin{aligned} \pi'_1(p_1,p_2) &=& 0 \\ \pi'_2(p_1,p_2) &=& 0 \end{aligned}\] besitzt genau eine Lösung, nämlich \[\begin{aligned} \left( \begin{array}{c} p_1 \\ p_2 \end{array} \right) &=& \left( \begin{array}{r} 5.451724 \\ 6.972414 \end{array} \right). \end{aligned}\] Es gibt also zunächst einmal genau einen stationären Punkt, weiters ist die Hesse-Matrix von \(\pi\) in jedem Punkt negativ semidefinit, da gilt: \[\begin{aligned} a_{11} &=& -46 < 0 \\ \det(\pi'') &=& (-46 \cdot (-14)) - (8 \cdot 8) = 580 \geq 0 \end{aligned}\] Die Funktion \(\pi\) ist also konkav, weshalb dieser stationäre Punkt bereits ein globaler Maximierer ist. Für die optimale Preiskombination \[\begin{aligned} \left( \begin{array}{c} p_1 \\ p_2 \end{array} \right) &=& \left( \begin{array}{r} 5.451724 \\ 6.972414 \end{array} \right) \end{aligned}\] erhalten wir nun \[\begin{aligned} q_{2}(p_1,p_2) &=& 96 -6 p_{1} -7 p_{2} = \\ &\approx& 14.48. \end{aligned}\] Bei einer Verkaufsmenge von \(q_{2}(p_1, p_2) = 14.48\) wird maximaler Gewinn erzielt.
Ein Monopolunternehmen bietet zwei Güter \(A\) und \(B\) zu den (veränderbaren) Preisen \(p_1\) (Gut \(A\)) und \(p_2\) (Gut \(B\)) an. Die Nachfrage nach diesen beiden Gütern wird durch die beiden Nachfragefunktionen \[\begin{aligned} q_1(p_1,p_2) &=& 87 -47 p_{1}+ 7 p_{2}, \\ q_2(p_1,p_2) &=& 63+ 4 p_{1} -4 p_{2} \end{aligned}\] bestimmt, wobei \(q_1\) die Nachfrage nach Gut \(A\) und \(q_2\) die Nachfrage nach Gut \(B\) beschreibt. Die Herstellungskosten für die beiden Güter betragen pro Stück \(1\) GE (Gut \(A\)) und \(3\) GE (Gut \(B\)). Es gibt ein eindeutig bestimmtes Paar \((p_1, p_2)\) von Preisen für die beiden Güter \(A\) und \(B\), sodass das Unternehmen maximalen Gewinn erzielt.
Wie groß ist die Verkaufsmenge \(q_{2}(p_1,p_2)\), wenn die Preise \(p_1\) und \(p_2\) so gewählt werden, dass maximaler Gewinn erzielt wird?
Für den erzielten Gewinn \(\pi\) in Abhängigkeit von den gewählten Preisen \(p_1\) und \(p_2\) erhalten wir \[\begin{aligned} \pi(p_1,p_2) &=& p_1 \cdot q_1(p_1,p_2) + p_2 \cdot q_2(p_1,p_2) - 1 \cdot q_1(p_1,p_2) - 3 \cdot q_2(p_1,p_2) = \\ &=& -276+ 122 p_{1}+ 68 p_{2} -47 p_{1}^{2} -4 p_{2}^{2}+ 11 p_{1} p_{2}. \end{aligned}\] Die partiellen Ableitungen von \(\pi\) sind \[\begin{aligned} \pi'_1(p_1,p_2) &=& 122 -94 p_{1}+ 11 p_{2}, \\ \pi'_2(p_1,p_2) &=& 68+ 11 p_{1} -8 p_{2}, \end{aligned}\] die Hesse-Matrix von \(\pi\) ist \[\begin{aligned} \pi''(p_1,p_2) = \left( \begin{array}{rr} -94 & 11 \\ 11 & -8 \end{array} \right). \end{aligned}\] Daraus erkennen wir, dass die Funktion \(\pi\) tatsächlich genau einen globalen Maximierer besitzt, denn das (lineare) Gleichungssystem \[\begin{aligned} \pi'_1(p_1,p_2) &=& 0 \\ \pi'_2(p_1,p_2) &=& 0 \end{aligned}\] besitzt genau eine Lösung, nämlich \[\begin{aligned} \left( \begin{array}{c} p_1 \\ p_2 \end{array} \right) &=& \left( \begin{array}{r} 2.732171 \\ 12.256735 \end{array} \right). \end{aligned}\] Es gibt also zunächst einmal genau einen stationären Punkt, weiters ist die Hesse-Matrix von \(\pi\) in jedem Punkt negativ semidefinit, da gilt: \[\begin{aligned} a_{11} &=& -94 < 0 \\ \det(\pi'') &=& (-94 \cdot (-8)) - (11 \cdot 11) = 631 \geq 0 \end{aligned}\] Die Funktion \(\pi\) ist also konkav, weshalb dieser stationäre Punkt bereits ein globaler Maximierer ist. Für die optimale Preiskombination \[\begin{aligned} \left( \begin{array}{c} p_1 \\ p_2 \end{array} \right) &=& \left( \begin{array}{r} 2.732171 \\ 12.256735 \end{array} \right) \end{aligned}\] erhalten wir nun \[\begin{aligned} q_{2}(p_1,p_2) &=& 63+ 4 p_{1} -4 p_{2} = \\ &\approx& 24.90. \end{aligned}\] Bei einer Verkaufsmenge von \(q_{2}(p_1, p_2) = 24.90\) wird maximaler Gewinn erzielt.
Ein Monopolunternehmen bietet zwei Güter \(A\) und \(B\) zu den (veränderbaren) Preisen \(p_1\) (Gut \(A\)) und \(p_2\) (Gut \(B\)) an. Die Nachfrage nach diesen beiden Gütern wird durch die beiden Nachfragefunktionen \[\begin{aligned} q_1(p_1,p_2) &=& 66 -21 p_{1}+ 4 p_{2}, \\ q_2(p_1,p_2) &=& 69 -2 p_{2} \end{aligned}\] bestimmt, wobei \(q_1\) die Nachfrage nach Gut \(A\) und \(q_2\) die Nachfrage nach Gut \(B\) beschreibt. Die Herstellungskosten für die beiden Güter betragen pro Stück \(1\) GE (Gut \(A\)) und \(10\) GE (Gut \(B\)). Es gibt ein eindeutig bestimmtes Paar \((p_1, p_2)\) von Preisen für die beiden Güter \(A\) und \(B\), sodass das Unternehmen maximalen Gewinn erzielt.
Wie groß ist die Verkaufsmenge \(q_{2}(p_1,p_2)\), wenn die Preise \(p_1\) und \(p_2\) so gewählt werden, dass maximaler Gewinn erzielt wird?
Für den erzielten Gewinn \(\pi\) in Abhängigkeit von den gewählten Preisen \(p_1\) und \(p_2\) erhalten wir \[\begin{aligned} \pi(p_1,p_2) &=& p_1 \cdot q_1(p_1,p_2) + p_2 \cdot q_2(p_1,p_2) - 1 \cdot q_1(p_1,p_2) - 10 \cdot q_2(p_1,p_2) = \\ &=& -756+ 87 p_{1}+ 85 p_{2} -21 p_{1}^{2} -2 p_{2}^{2}+ 4 p_{1} p_{2}. \end{aligned}\] Die partiellen Ableitungen von \(\pi\) sind \[\begin{aligned} \pi'_1(p_1,p_2) &=& 87 -42 p_{1}+ 4 p_{2}, \\ \pi'_2(p_1,p_2) &=& 85+ 4 p_{1} -4 p_{2}, \end{aligned}\] die Hesse-Matrix von \(\pi\) ist \[\begin{aligned} \pi''(p_1,p_2) = \left( \begin{array}{rr} -42 & 4 \\ 4 & -4 \end{array} \right). \end{aligned}\] Daraus erkennen wir, dass die Funktion \(\pi\) tatsächlich genau einen globalen Maximierer besitzt, denn das (lineare) Gleichungssystem \[\begin{aligned} \pi'_1(p_1,p_2) &=& 0 \\ \pi'_2(p_1,p_2) &=& 0 \end{aligned}\] besitzt genau eine Lösung, nämlich \[\begin{aligned} \left( \begin{array}{c} p_1 \\ p_2 \end{array} \right) &=& \left( \begin{array}{r} 4.526316 \\ 25.776316 \end{array} \right). \end{aligned}\] Es gibt also zunächst einmal genau einen stationären Punkt, weiters ist die Hesse-Matrix von \(\pi\) in jedem Punkt negativ semidefinit, da gilt: \[\begin{aligned} a_{11} &=& -42 < 0 \\ \det(\pi'') &=& (-42 \cdot (-4)) - (4 \cdot 4) = 152 \geq 0 \end{aligned}\] Die Funktion \(\pi\) ist also konkav, weshalb dieser stationäre Punkt bereits ein globaler Maximierer ist. Für die optimale Preiskombination \[\begin{aligned} \left( \begin{array}{c} p_1 \\ p_2 \end{array} \right) &=& \left( \begin{array}{r} 4.526316 \\ 25.776316 \end{array} \right) \end{aligned}\] erhalten wir nun \[\begin{aligned} q_{2}(p_1,p_2) &=& 69 -2 p_{2} = \\ &\approx& 17.45. \end{aligned}\] Bei einer Verkaufsmenge von \(q_{2}(p_1, p_2) = 17.45\) wird maximaler Gewinn erzielt.
Ein Monopolist bietet zwei Güter zu den Preisen \(p_1\) und \(p_2\) an. Das Unternehemen X überlegt in den Markt für die beiden Güter einzutreten. Das Unternehmen kennt die Auswirkung der Eigenpreise auf die Nachfrage der jeweiligen Güter. Es weiß aber nicht, wie sich die Kreuzpreise auswirken. Um die richtige Entscheidung treffen zu können, wäre es vorteilhaft, die Kreuzpreiselastizität zu kennen. Die Nachfragefunktionen besitzen die Form: \[\begin{aligned}
q_1 &=& D_1(p_1, p_2) = 188 - 8 p_1 + b p_2\\
q_2 &=& D_2(p_1, p_2) = 126 + a p_1 - 8p_2
\end{aligned}\] Man kann davon ausgehen, dass der Monopolist einen maximalen Gewinn bei einer Preissetzung von \(p_1 = 62\) GE und \(p_2 = 61\) GE erzielt. Die Herstellungskosten pro Stück für Gut 1 betragen \(2\) GE. Für Gut 2 \(4\) GE.
Um wieviele Einheiten verändert sich die Nachfrage nach \(q_1\), wenn der Preis für \(q_2\) um eine GE steigt?
Der Gewinn ergibt sich aus dem Erlös abzüglich der Kosten. Daher ist \[\begin{aligned} \pi (p_1, p_2) &=& q_1(p_1, p_2) \cdot p_1 + q_2(p_1, p_2) \cdot p_2 - (q_1(p_1, p_2) \cdot k_1 + q_2(p_1, p_2) \cdot k_2)\\ \pi (p_1, p_2) &=& -8p_1^2 - 8p_2^2 + (b+a)p_1 p_2 + (204-4a)p_1 + (158-2b)p_2 - 880 \end{aligned}\]
Um den kritischen Punkt zu erhalten, werden die partiellen Ableitungen 1. Ordnung berechnet und gleich Null gesetzt: \[\begin{aligned} \pi_1' (p_1, p_2) &=& -16p_1 + (b+a)p_2 + (204-4a) = 0\\ \pi_2' (p_1, p_2) &=& -16p_2 + (b+a)p_1 + (158-2b) = 0 \end{aligned}\] Nun können wir die Preise, bei welchen der Gewinn maximiert wird, in die partiellen Ableitungen 1. Ordnung einsetzen. \[\begin{aligned} \pi_1' (p_1, p_2) &=& 61b + 57a - 788 = 0\\ \pi_2' (p_1, p_2) &=& 60b + 62a - 818 = 0 \end{aligned}\]
Durch Lösen des Gleichungssystems erhalten wir die beiden fehlenden Parameter \(a = 7.232044\) und \(b = 6.160221\).
Um zu überprüfen, ob dieser kritische Punkt ein globales Maximum ist, berechnet man die Hesse-Matrix: \[\begin{aligned}
\pi'' (p_1, p_2) = \mathbf{A} = \left( \begin{array}{rr} -16.000000 & 13.392265 \\ 13.392265 & -16.000000 \end{array} \right)
\end{aligned}\]
Da \(a_{11} = -16 < 0\) und \(\\\\det \mathbf{A} = 76.65 \geq 0\) ist \(\mathbf{A}\) negativ semidefinit. Daher ist der kritische Punkt \(p_1 = 62\) und \(p_2 = 61\) ein globales Maximum.
Die Nachfrage nach \(q_1\) steigt um \(6.16\) Einheiten, wenn sich der Preis für \(q_2\) um eine GE erhöht.
Ein Monopolist bietet zwei Güter zu den Preisen \(p_1\) und \(p_2\) an. Das Unternehemen X überlegt in den Markt für die beiden Güter einzutreten. Das Unternehmen kennt die Auswirkung der Eigenpreise auf die Nachfrage der jeweiligen Güter. Es weiß aber nicht, wie sich die Kreuzpreise auswirken. Um die richtige Entscheidung treffen zu können, wäre es vorteilhaft, die Kreuzpreiselastizität zu kennen. Die Nachfragefunktionen besitzen die Form: \[\begin{aligned}
q_1 &=& D_1(p_1, p_2) = 168 - 8 p_1 + b p_2\\
q_2 &=& D_2(p_1, p_2) = 100 + a p_1 - 8p_2
\end{aligned}\] Man kann davon ausgehen, dass der Monopolist einen maximalen Gewinn bei einer Preissetzung von \(p_1 = 50\) GE und \(p_2 = 48\) GE erzielt. Die Herstellungskosten pro Stück für Gut 1 betragen \(4\) GE. Für Gut 2 \(5\) GE.
Um wieviele Einheiten verändert sich die Nachfrage nach \(q_2\), wenn der Preis für \(q_1\) um eine GE steigt?
Der Gewinn ergibt sich aus dem Erlös abzüglich der Kosten. Daher ist \[\begin{aligned} \pi (p_1, p_2) &=& q_1(p_1, p_2) \cdot p_1 + q_2(p_1, p_2) \cdot p_2 - (q_1(p_1, p_2) \cdot k_1 + q_2(p_1, p_2) \cdot k_2)\\ \pi (p_1, p_2) &=& -8p_1^2 - 8p_2^2 + (b+a)p_1 p_2 + (200-5a)p_1 + (140-4b)p_2 - 1172 \end{aligned}\]
Um den kritischen Punkt zu erhalten, werden die partiellen Ableitungen 1. Ordnung berechnet und gleich Null gesetzt: \[\begin{aligned} \pi_1' (p_1, p_2) &=& -16p_1 + (b+a)p_2 + (200-5a) = 0\\ \pi_2' (p_1, p_2) &=& -16p_2 + (b+a)p_1 + (140-4b) = 0 \end{aligned}\] Nun können wir die Preise, bei welchen der Gewinn maximiert wird, in die partiellen Ableitungen 1. Ordnung einsetzen. \[\begin{aligned} \pi_1' (p_1, p_2) &=& 48b + 43a - 600 = 0\\ \pi_2' (p_1, p_2) &=& 46b + 50a - 628 = 0 \end{aligned}\]
Durch Lösen des Gleichungssystems erhalten wir die beiden fehlenden Parameter \(a = 6.028436\) und \(b = 7.099526\).
Um zu überprüfen, ob dieser kritische Punkt ein globales Maximum ist, berechnet man die Hesse-Matrix: \[\begin{aligned}
\pi'' (p_1, p_2) = \mathbf{A} = \left( \begin{array}{rr} -16.000000 & 13.127962 \\ 13.127962 & -16.000000 \end{array} \right)
\end{aligned}\]
Da \(a_{11} = -16 < 0\) und \(\\\\det \mathbf{A} = 83.66 \geq 0\) ist \(\mathbf{A}\) negativ semidefinit. Daher ist der kritische Punkt \(p_1 = 50\) und \(p_2 = 48\) ein globales Maximum.
Die Nachfrage nach \(q_2\) steigt um \(6.03\) Einheiten, wenn sich der Preis für \(q_1\) um eine GE erhöht.
Ein Monopolist bietet zwei Güter zu den Preisen \(p_1\) und \(p_2\) an. Das Unternehemen X überlegt in den Markt für die beiden Güter einzutreten. Das Unternehmen kennt die Auswirkung der Eigenpreise auf die Nachfrage der jeweiligen Güter. Es weiß aber nicht, wie sich die Kreuzpreise auswirken. Um die richtige Entscheidung treffen zu können, wäre es vorteilhaft, die Kreuzpreiselastizität zu kennen. Die Nachfragefunktionen besitzen die Form: \[\begin{aligned}
q_1 &=& D_1(p_1, p_2) = 190 - 6 p_1 + b p_2\\
q_2 &=& D_2(p_1, p_2) = 110 + a p_1 - 6p_2
\end{aligned}\] Man kann davon ausgehen, dass der Monopolist einen maximalen Gewinn bei einer Preissetzung von \(p_1 = 55\) GE und \(p_2 = 51\) GE erzielt. Die Herstellungskosten pro Stück für Gut 1 betragen \(3\) GE. Für Gut 2 \(2\) GE.
Um wieviele Einheiten verändert sich die Nachfrage nach \(q_1\), wenn der Preis für \(q_2\) um eine GE steigt?
Der Gewinn ergibt sich aus dem Erlös abzüglich der Kosten. Daher ist \[\begin{aligned} \pi (p_1, p_2) &=& q_1(p_1, p_2) \cdot p_1 + q_2(p_1, p_2) \cdot p_2 - (q_1(p_1, p_2) \cdot k_1 + q_2(p_1, p_2) \cdot k_2)\\ \pi (p_1, p_2) &=& -6p_1^2 - 6p_2^2 + (b+a)p_1 p_2 + (208-2a)p_1 + (122-3b)p_2 - 790 \end{aligned}\]
Um den kritischen Punkt zu erhalten, werden die partiellen Ableitungen 1. Ordnung berechnet und gleich Null gesetzt: \[\begin{aligned} \pi_1' (p_1, p_2) &=& -12p_1 + (b+a)p_2 + (208-2a) = 0\\ \pi_2' (p_1, p_2) &=& -12p_2 + (b+a)p_1 + (122-3b) = 0 \end{aligned}\] Nun können wir die Preise, bei welchen der Gewinn maximiert wird, in die partiellen Ableitungen 1. Ordnung einsetzen. \[\begin{aligned} \pi_1' (p_1, p_2) &=& 51b + 49a - 452 = 0\\ \pi_2' (p_1, p_2) &=& 52b + 55a - 490 = 0 \end{aligned}\]
Durch Lösen des Gleichungssystems erhalten wir die beiden fehlenden Parameter \(a = 5.782101\) und \(b = 3.307393\).
Um zu überprüfen, ob dieser kritische Punkt ein globales Maximum ist, berechnet man die Hesse-Matrix: \[\begin{aligned}
\pi'' (p_1, p_2) = \mathbf{A} = \left( \begin{array}{rr} -12.000000 & 9.089494 \\ 9.089494 & -12.000000 \end{array} \right)
\end{aligned}\]
Da \(a_{11} = -12 < 0\) und \(\\\\det \mathbf{A} = 61.38 \geq 0\) ist \(\mathbf{A}\) negativ semidefinit. Daher ist der kritische Punkt \(p_1 = 55\) und \(p_2 = 51\) ein globales Maximum.
Die Nachfrage nach \(q_1\) steigt um \(3.31\) Einheiten, wenn sich der Preis für \(q_2\) um eine GE erhöht.
Kettenregel und implizite Funktionen
Ein Unternehmen stellt ein Gut aus zwei Rohstoffen \(A\) und \(B\) her. Die herstellbare Menge des Gutes hängt ab von den Mengen an eingesetzten Rohstoffen gemäß der Produktionsfunktion \[\begin{aligned} q = F(x_1, x_2) = 13 x_1^{0.59} x_2^{0.29}. \end{aligned}\] Dabei bezeichnen \(x_1\) und \(x_2\) die eingesetzten Mengen der Rohstoffe \(A\) und \(B\) und \({q = F(x_1, x_2)}\) die pro Monat hergestellte Menge des Produkts. Im Moment verwendet der Hersteller die Faktorkombination \((x_1, x_2) = (7, 6)\).
Bestimmen Sie die momentane Änderungsrate von Faktor \(B\) bei Erhöhung von Faktor \(A\) um eine marginale Einheit und unter Beibehaltung des Produktionsniveaus von \(F(7, 6)\) Mengeneinheiten.
Der Hersteller möchte die Faktorkombination so ändern, dass der Output gleich bleibt. Der Produktionsfaktor \(A\) wird um eine marginale Einheit erhöht. Damit wird \(x_1\) als Menge des Produktionsfaktors \(A\) vom Hersteller festgelegt und er muss die Menge \(x_2\) so berechnen, dass der Output unverändert bleibt. Das heißt wir benötigen folgende Gleichung \[\begin{aligned} f'(x_1) = - \frac{F'_1(x_1, x_2)}{F'_2(x_1, x_2)}. \end{aligned}\] Die partiellen Ableitungen \(F'_1(x_1,x_2)\) und \(F'_2(x_1,x_2)\) sind \[\begin{aligned} F'_1(x_1,x_2) = 13\cdot0.59x_1^{-0.41}x_2^{0.29}\\ F'_2(x_1,x_2) = 13\cdot0.29x_1^{0.59}x_2^{-0.71}. \end{aligned}\] Daraus folgt \[\begin{aligned} f'(7) & = & - \frac{F'_1(7, 6)}{F'_2(7, 6)} \\ & = & - \frac{13 \cdot 0.59 \cdot 7^{0.59 - 1} \cdot 6^{0.29}}{13 \cdot 0.29 \cdot 7^{0.59} \cdot 6^{0.29 - 1}} \\ & = & -1.743842. \end{aligned}\] Wird der Produktionsfaktor \(A\) um eine marginale Einheit erhöht, dann kann der Produktionsfaktor \(B\) um \(-1.74\) verändert werden unter Beibehaltung des Produktionsniveaus.
Ein Unternehmen stellt ein Gut aus zwei Rohstoffen \(A\) und \(B\) her. Die herstellbare Menge des Gutes hängt ab von den Mengen an eingesetzten Rohstoffen gemäß der Produktionsfunktion \[\begin{aligned} q = F(x_1, x_2) = 7 x_1^{0.69} x_2^{0.19}. \end{aligned}\] Dabei bezeichnen \(x_1\) und \(x_2\) die eingesetzten Mengen der Rohstoffe \(A\) und \(B\) und \({q = F(x_1, x_2)}\) die pro Monat hergestellte Menge des Produkts. Im Moment verwendet der Hersteller die Faktorkombination \((x_1, x_2) = (8, 8)\).
Bestimmen Sie die momentane Änderungsrate von Faktor \(B\) bei Erhöhung von Faktor \(A\) um eine marginale Einheit und unter Beibehaltung des Produktionsniveaus von \(F(8, 8)\) Mengeneinheiten.
Der Hersteller möchte die Faktorkombination so ändern, dass der Output gleich bleibt. Der Produktionsfaktor \(A\) wird um eine marginale Einheit erhöht. Damit wird \(x_1\) als Menge des Produktionsfaktors \(A\) vom Hersteller festgelegt und er muss die Menge \(x_2\) so berechnen, dass der Output unverändert bleibt. Das heißt wir benötigen folgende Gleichung \[\begin{aligned} f'(x_1) = - \frac{F'_1(x_1, x_2)}{F'_2(x_1, x_2)}. \end{aligned}\] Die partiellen Ableitungen \(F'_1(x_1,x_2)\) und \(F'_2(x_1,x_2)\) sind \[\begin{aligned} F'_1(x_1,x_2) = 7\cdot0.69x_1^{-0.31}x_2^{0.19}\\ F'_2(x_1,x_2) = 7\cdot0.19x_1^{0.69}x_2^{-0.81}. \end{aligned}\] Daraus folgt \[\begin{aligned} f'(8) & = & - \frac{F'_1(8, 8)}{F'_2(8, 8)} \\ & = & - \frac{7 \cdot 0.69 \cdot 8^{0.69 - 1} \cdot 8^{0.19}}{7 \cdot 0.19 \cdot 8^{0.69} \cdot 8^{0.19 - 1}} \\ & = & -3.631579. \end{aligned}\] Wird der Produktionsfaktor \(A\) um eine marginale Einheit erhöht, dann kann der Produktionsfaktor \(B\) um \(-3.63\) verändert werden unter Beibehaltung des Produktionsniveaus.
Ein Unternehmen stellt ein Gut aus zwei Rohstoffen \(A\) und \(B\) her. Die herstellbare Menge des Gutes hängt ab von den Mengen an eingesetzten Rohstoffen gemäß der Produktionsfunktion \[\begin{aligned} q = F(x_1, x_2) = 8 x_1^{0.65} x_2^{0.23}. \end{aligned}\] Dabei bezeichnen \(x_1\) und \(x_2\) die eingesetzten Mengen der Rohstoffe \(A\) und \(B\) und \({q = F(x_1, x_2)}\) die pro Monat hergestellte Menge des Produkts. Im Moment verwendet der Hersteller die Faktorkombination \((x_1, x_2) = (9, 7)\).
Bestimmen Sie die momentane Änderungsrate von Faktor \(A\) bei Erhöhung von Faktor \(B\) um eine marginale Einheit und unter Beibehaltung des Produktionsniveaus von \(F(9, 7)\) Mengeneinheiten.
Der Hersteller möchte die Faktorkombination so ändern, dass der Output gleich bleibt. Der Produktionsfaktor \(B\) wird um eine marginale Einheit erhöht. Damit wird \(x_2\) als Menge des Produktionsfaktors \(B\) vom Hersteller festgelegt und er muss die Menge \(x_1\) so berechnen, dass der Output unverändert bleibt. Das heißt wir benötigen folgende Gleichung \[\begin{aligned} f'(x_2) = - \frac{F'_2(x_1, x_2)}{F'_1(x_1, x_2)}. \end{aligned}\] Die partiellen Ableitungen \(F'_1(x_1,x_2)\) und \(F'_2(x_1,x_2)\) sind \[\begin{aligned} F'_1(x_1,x_2) = 8\cdot0.65x_1^{-0.35}x_2^{0.23}\\ F'_2(x_1,x_2) = 8\cdot0.23x_1^{0.65}x_2^{-0.77}. \end{aligned}\] Daraus folgt \[\begin{aligned} f'(7) & = & - \frac{F'_2(9, 7)}{F'_1(9, 7)} \\ & = & - \frac{8 \cdot 0.23 \cdot 9^{0.65} \cdot 7^{0.23 - 1}}{8 \cdot 0.65 \cdot 9^{0.65 - 1} \cdot 7^{0.23}} \\ & = & -0.454945. \end{aligned}\] Wird der Produktionsfaktor \(B\) um eine marginale Einheit erhöht, dann kann der Produktionsfaktor \(A\) um \(-0.45\) verändert werden unter Beibehaltung des Produktionsniveaus.
Ein Unternehmen stellt ein Gut aus zwei Rohstoffen \(A\) und \(B\) her. Die herstellbare Menge des Gutes hängt ab von den Mengen an eingesetzten Rohstoffen gemäß der Produktionsfunktion \[\begin{aligned} q = F(x_1, x_2) = e^{0.45 x_1 + 0.05 x_2 + 0.3 x_1 x_2}. \end{aligned}\] Dabei bezeichnen \(x_1\) und \(x_2\) die eingesetzten Mengen der Rohstoffe \(A\) und \(B\) und \({q = F(x_1, x_2)}\) die pro Monat hergestellte Menge des Produkts. Im Moment verwendet der Hersteller die Faktorkombination \((x_1, x_2) = (2.3, 1.9)\).
Bestimmen Sie die momentane Änderungsrate von Faktor \(A\) bei Erhöhung von Faktor \(B\) um eine marginale Einheit und unter Beibehaltung des Produktionsniveaus von \(F(2.3, 1.9)\) Mengeneinheiten.
Der Hersteller möchte die Faktorkombination so ändern, dass der Output gleich bleibt. Der Produktionsfaktor \(B\) wird um eine marginale Einheit erhöht. Damit wird \(x_2\) als Menge des Produktionsfaktors \(B\) vom Hersteller festgelegt und er muss die Menge \(x_1\) so berechnen, dass der Output unverändert bleibt. Das heißt wir benötigen folgende Gleichung \[\begin{aligned} f'(x_2) = - \frac{F'_2(x_1, x_2)}{F'_1(x_1, x_2)}. \end{aligned}\] Die partiellen Ableitungen \(F'_1(x_1,x_2)\) und \(F'_2(x_1,x_2)\) sind \[\begin{aligned} F'_1(x_1, x_2) &=& e^{0.45 x_1 + 0.05 x_2 + 0.3 x_1 x_2} \cdot \left( 0.45 + 0.3 x_2 \right) \\ F'_2(x_1, x_2) &=& e^{0.45 x_1 + 0.05 x_2 + 0.3 x_1 x_2} \cdot \left( 0.05 + 0.3 x_1 \right). \end{aligned}\] Daraus folgt \[\begin{aligned} f'(1.9) & = & - \frac{F'_2(2.3, 1.9)}{F'_1(2.3, 1.9)} \\ & = & - \frac{e^{0.45 \cdot 2.3 + 0.05 \cdot 1.9 + 0.3 \cdot 2.3 \cdot 1.9} \cdot \left( 0.05 + 0.3 \cdot 2.3 \right)}{e^{0.45 \cdot 2.3 + 0.05 \cdot 1.9 + 0.3 \cdot 2.3 \cdot 1.9} \cdot \left( 0.45 + 0.3 \cdot 1.9 \right)} \\ & = & -0.72549. \end{aligned}\] Wird der Produktionsfaktor \(B\) um eine marginale Einheit erhöht, dann kann der Produktionsfaktor \(A\) um \(-0.73\) verändert werden unter Beibehaltung des Produktionsniveaus.
Ein Unternehmen stellt ein Gut aus zwei Rohstoffen \(A\) und \(B\) her. Die herstellbare Menge des Gutes hängt ab von den Mengen an eingesetzten Rohstoffen gemäß der Produktionsfunktion \[\begin{aligned} q = F(x_1, x_2) = e^{0.1 x_1 + 0.35 x_2 + 0.1 x_1 x_2}. \end{aligned}\] Dabei bezeichnen \(x_1\) und \(x_2\) die eingesetzten Mengen der Rohstoffe \(A\) und \(B\) und \({q = F(x_1, x_2)}\) die pro Monat hergestellte Menge des Produkts. Im Moment verwendet der Hersteller die Faktorkombination \((x_1, x_2) = (2.6, 1.4)\).
Bestimmen Sie die momentane Änderungsrate von Faktor \(B\) bei Erhöhung von Faktor \(A\) um eine marginale Einheit und unter Beibehaltung des Produktionsniveaus von \(F(2.6, 1.4)\) Mengeneinheiten.
Der Hersteller möchte die Faktorkombination so ändern, dass der Output gleich bleibt. Der Produktionsfaktor \(A\) wird um eine marginale Einheit erhöht. Damit wird \(x_1\) als Menge des Produktionsfaktors \(A\) vom Hersteller festgelegt und er muss die Menge \(x_2\) so berechnen, dass der Output unverändert bleibt. Das heißt wir benötigen folgende Gleichung \[\begin{aligned} f'(x_1) = - \frac{F'_1(x_1, x_2)}{F'_2(x_1, x_2)}. \end{aligned}\] Die partiellen Ableitungen \(F'_1(x_1,x_2)\) und \(F'_2(x_1,x_2)\) sind \[\begin{aligned} F'_1(x_1, x_2) &=& e^{0.1 x_1 + 0.35 x_2 + 0.1 x_1 x_2} \cdot \left( 0.1 + 0.1 x_2 \right) \\ F'_2(x_1, x_2) &=& e^{0.1 x_1 + 0.35 x_2 + 0.1 x_1 x_2} \cdot \left( 0.35 + 0.1 x_1 \right). \end{aligned}\] Daraus folgt \[\begin{aligned} f'(2.6) & = & - \frac{F'_1(2.6, 1.4)}{F'_2(2.6, 1.4)} \\ & = & - \frac{e^{0.1 \cdot 2.6 + 0.35 \cdot 1.4 + 0.1 \cdot 2.6 \cdot 1.4} \cdot \left( 0.1 + 0.1 \cdot 1.4 \right)}{e^{0.1 \cdot 2.6 + 0.35 \cdot 1.4 + 0.1 \cdot 2.6 \cdot 1.4} \cdot \left( 0.35 + 0.1 \cdot 2.6 \right)} \\ & = & -0.393443. \end{aligned}\] Wird der Produktionsfaktor \(A\) um eine marginale Einheit erhöht, dann kann der Produktionsfaktor \(B\) um \(-0.39\) verändert werden unter Beibehaltung des Produktionsniveaus.
Ein Unternehmen stellt ein Gut aus zwei Rohstoffen \(A\) und \(B\) her. Die herstellbare Menge des Gutes hängt ab von den Mengen an eingesetzten Rohstoffen gemäß der Produktionsfunktion \[\begin{aligned} q = F(x_1, x_2) = e^{0.2 x_1 + 0.05 x_2 + 0.4 x_1 x_2}. \end{aligned}\] Dabei bezeichnen \(x_1\) und \(x_2\) die eingesetzten Mengen der Rohstoffe \(A\) und \(B\) und \({q = F(x_1, x_2)}\) die pro Monat hergestellte Menge des Produkts. Im Moment verwendet der Hersteller die Faktorkombination \((x_1, x_2) = (1.4, 1.9)\).
Bestimmen Sie die momentane Änderungsrate von Faktor \(B\) bei Erhöhung von Faktor \(A\) um eine marginale Einheit und unter Beibehaltung des Produktionsniveaus von \(F(1.4, 1.9)\) Mengeneinheiten.
Der Hersteller möchte die Faktorkombination so ändern, dass der Output gleich bleibt. Der Produktionsfaktor \(A\) wird um eine marginale Einheit erhöht. Damit wird \(x_1\) als Menge des Produktionsfaktors \(A\) vom Hersteller festgelegt und er muss die Menge \(x_2\) so berechnen, dass der Output unverändert bleibt. Das heißt wir benötigen folgende Gleichung \[\begin{aligned} f'(x_1) = - \frac{F'_1(x_1, x_2)}{F'_2(x_1, x_2)}. \end{aligned}\] Die partiellen Ableitungen \(F'_1(x_1,x_2)\) und \(F'_2(x_1,x_2)\) sind \[\begin{aligned} F'_1(x_1, x_2) &=& e^{0.2 x_1 + 0.05 x_2 + 0.4 x_1 x_2} \cdot \left( 0.2 + 0.4 x_2 \right) \\ F'_2(x_1, x_2) &=& e^{0.2 x_1 + 0.05 x_2 + 0.4 x_1 x_2} \cdot \left( 0.05 + 0.4 x_1 \right). \end{aligned}\] Daraus folgt \[\begin{aligned} f'(1.4) & = & - \frac{F'_1(1.4, 1.9)}{F'_2(1.4, 1.9)} \\ & = & - \frac{e^{0.2 \cdot 1.4 + 0.05 \cdot 1.9 + 0.4 \cdot 1.4 \cdot 1.9} \cdot \left( 0.2 + 0.4 \cdot 1.9 \right)}{e^{0.2 \cdot 1.4 + 0.05 \cdot 1.9 + 0.4 \cdot 1.4 \cdot 1.9} \cdot \left( 0.05 + 0.4 \cdot 1.4 \right)} \\ & = & -1.57377. \end{aligned}\] Wird der Produktionsfaktor \(A\) um eine marginale Einheit erhöht, dann kann der Produktionsfaktor \(B\) um \(-1.57\) verändert werden unter Beibehaltung des Produktionsniveaus.
Ein Hersteller produziert ein Gut aus den Rohstoffen \(A\) und \(B\). Die Produktionsfunktion lautet \[\begin{aligned} q = F(x_1, x_2) = 9 \cdot x_1^{2} + 1 \cdot x_1 \cdot x_2 + 6 \cdot x_2^{2}, \end{aligned}\] wobei \(x_1\) die eingesetzte Menge von Produktionsfaktor \(A\) und \(x_2\) die eingesetzte Menge von Produktionsfaktor \(B\) bezeichnet. Im Moment verwendet der Hersteller die Faktorkombination \((x_1, x_2) = (8, 9)\).
Bestimmen Sie die exakte Veränderung von Faktor \(B\), wenn sich Faktor \(A\) um \(0.25\) Einheiten an der Stelle \(\mathbf{a} = (8, 9)^\top\) und unter Beibehaltung des Produktionsniveaus der Funktion \(F(\mathbf{a})\) erhöht. (Gehen Sie außerdem davon aus, dass \(x_1 \geq 0\) und \(x_2 \geq 0\) gilt.)
Exakte Veränderung:
Der Hersteller möchte die Faktorkombination so ändern, dass der Output gleich bleibt. Der Produktionsfaktor \(A\) erhöht sich um \(0.25\) Einheiten. Damit wird \(x_1\) als Menge des Produktionsfaktors \(A\) vom Hersteller festgelegt und er muss die Menge \(x_2\) so berechnen, dass der Output unverändert bleibt. Für die explizite Darstellung der Funktion \(f\) bzw. die Gleichung der Isoquante wird also die Funktionsgleichung dem beizubehaltenden Niveau gleichgesetzt und \(x_2\) freigestellt. Man verwendet dann folgenden Zusammenhang: \(x_2=f(x_1)\) \[\begin{aligned} F(x_1, x_2) & = & 9 \cdot x_1^{2} + 1 \cdot x_1 \cdot x_2 + 6 \cdot x_2^{2}\\ 1134 &=& F(8,9)\\ 1134 &=& 9 \cdot x_1^{2} + 1 \cdot x_1 \cdot x_2 + 6 \cdot x_2^{2}\\ 1134 &=& 6 \cdot x_2^{2} + 1 \cdot x_1 \cdot x_2 + 9 \cdot x_1^{2}\\ 0 &=& x_2^{2} + \frac{1}{6} \cdot x_1 \cdot x_2 + \frac{9}{6} \cdot x_1^{2} - \frac{1134}{6}\\ x_{2_{1,2}}&=&-\frac{1}{2\cdot6}x_1 \pm \sqrt{\left(\frac{1}{2\cdot 6}\right)^2x_1^2-\left(\frac{9}{6} \cdot x_1^{2} - \frac{1134}{6}\right)}\\ \end{aligned}\]
Wegen \(x_1 \geq 0\) und \(x_2 \geq 0\) sind wir nur an positiven Lösungen interessiert: \[\begin{aligned} x_2 = f(x_1) &=& -0.083333x_1 + \sqrt{-1.493056 \cdot x_1^{2} + 189} \end{aligned}\]
Zur Berechnung der exakten Veränderung von \(x_2\) wird die Differenz der Funktionswerte betrachtet:
\(x_1\) wird von \(8\) um \(0.25\) Einheiten auf \(8.25\) erhöht; damit muss \(x_2\) von \(f(8) = 9\) sinken auf:
\[\begin{aligned}
f(8.25) & = & -0.083333 \cdot 8.25 + \sqrt{-1.493056 \cdot 8.25^{2} + 189}\\ & = & 8.660168
\end{aligned}\] Also verändert sich \(x_2\) exakt um \(8.660168 - 9 = -0.339832 \approx -0.34\) Einheiten.
Ein Hersteller produziert ein Gut aus den Rohstoffen \(A\) und \(B\). Die Produktionsfunktion lautet \[\begin{aligned} q = F(x_1, x_2) = 6 \cdot x_1^{2} + 8 \cdot x_1 \cdot x_2 + 5 \cdot x_2^{2}, \end{aligned}\] wobei \(x_1\) die eingesetzte Menge von Produktionsfaktor \(A\) und \(x_2\) die eingesetzte Menge von Produktionsfaktor \(B\) bezeichnet. Im Moment verwendet der Hersteller die Faktorkombination \((x_1, x_2) = (2, 1)\).
Bestimmen Sie die exakte Veränderung von Faktor \(A\), wenn sich Faktor \(B\) um \(0.25\) Einheiten an der Stelle \(\mathbf{a} = (2, 1)^\top\) und unter Beibehaltung des Produktionsniveaus der Funktion \(F(\mathbf{a})\) erhöht. (Gehen Sie außerdem davon aus, dass \(x_1 \geq 0\) und \(x_2 \geq 0\) gilt.)
Exakte Veränderung:
Der Hersteller möchte die Faktorkombination so ändern, dass der Output gleich bleibt. Der Produktionsfaktor \(B\) erhöht sich um \(0.25\) Einheiten. Damit wird \(x_2\) als Menge des Produktionsfaktors \(B\) vom Hersteller festgelegt und er muss die Menge \(x_1\) so berechnen, dass der Output unverändert bleibt. Für die explizite Darstellung der Funktion \(f\) bzw. die Gleichung der Isoquante wird also die Funktionsgleichung dem beizubehaltenden Niveau gleichgesetzt und \(x_1\) freigestellt. Man verwendet dann folgenden Zusammenhang: \(x_1=f(x_2)\) \[\begin{aligned} F(x_1, x_2) & = & 6 \cdot x_1^{2} + 8 \cdot x_1 \cdot x_2 + 5 \cdot x_2^{2}\\ 45 &=& F(2,1)\\ 45 &=& 6 \cdot x_1^{2} + 8 \cdot x_1 \cdot x_2 + 5 \cdot x_2^{2}\\ 0 &=& x_1^{2} + \frac{8}{6} \cdot x_1 \cdot x_2 + \frac{5}{6} \cdot x_2^{2} - \frac{45}{6}\\ x_{1_{1,2}}&=&-\frac{8}{2\cdot6}x_2 \pm \sqrt{\left(\frac{8}{2\cdot 6}\right)^2x_2^2-\left(\frac{5}{6} \cdot x_2^{2} - \frac{45}{6}\right)}\\ \end{aligned}\]
Wegen \(x_1 \geq 0\) und \(x_2 \geq 0\) sind wir nur an positiven Lösungen interessiert: \[\begin{aligned} x_1 = f(x_2) &=& -0.666667x_2 + \sqrt{-0.388889 \cdot x_2^{2} + 7.5} \end{aligned}\]
Zur Berechnung der exakten Veränderung von \(x_1\) wird die Differenz der Funktionswerte betrachtet:
\(x_2\) wird von \(1\) um \(0.25\) Einheiten auf \(1.25\) erhöht; damit muss \(x_1\) von \(f(1) = 2\) sinken auf:
\[\begin{aligned}
f(1.25) & = & -0.666667 \cdot 1.25 + \sqrt{-0.388889 \cdot 1.25^{2} + 7.5}\\ & = & 1.791997
\end{aligned}\] Also verändert sich \(x_1\) exakt um \(1.791997 - 2 = -0.208003 \approx -0.21\) Einheiten.
Ein Hersteller produziert ein Gut aus den Rohstoffen \(A\) und \(B\). Die Produktionsfunktion lautet \[\begin{aligned} q = F(x_1, x_2) = 1 \cdot x_1^{2} + 6 \cdot x_1 \cdot x_2 + 6 \cdot x_2^{2}, \end{aligned}\] wobei \(x_1\) die eingesetzte Menge von Produktionsfaktor \(A\) und \(x_2\) die eingesetzte Menge von Produktionsfaktor \(B\) bezeichnet. Im Moment verwendet der Hersteller die Faktorkombination \((x_1, x_2) = (9, 2)\).
Bestimmen Sie die exakte Veränderung von Faktor \(B\), wenn sich Faktor \(A\) um \(0.3\) Einheiten an der Stelle \(\mathbf{a} = (9, 2)^\top\) und unter Beibehaltung des Produktionsniveaus der Funktion \(F(\mathbf{a})\) erhöht. (Gehen Sie außerdem davon aus, dass \(x_1 \geq 0\) und \(x_2 \geq 0\) gilt.)
Exakte Veränderung:
Der Hersteller möchte die Faktorkombination so ändern, dass der Output gleich bleibt. Der Produktionsfaktor \(A\) erhöht sich um \(0.3\) Einheiten. Damit wird \(x_1\) als Menge des Produktionsfaktors \(A\) vom Hersteller festgelegt und er muss die Menge \(x_2\) so berechnen, dass der Output unverändert bleibt. Für die explizite Darstellung der Funktion \(f\) bzw. die Gleichung der Isoquante wird also die Funktionsgleichung dem beizubehaltenden Niveau gleichgesetzt und \(x_2\) freigestellt. Man verwendet dann folgenden Zusammenhang: \(x_2=f(x_1)\) \[\begin{aligned} F(x_1, x_2) & = & 1 \cdot x_1^{2} + 6 \cdot x_1 \cdot x_2 + 6 \cdot x_2^{2}\\ 213 &=& F(9,2)\\ 213 &=& 1 \cdot x_1^{2} + 6 \cdot x_1 \cdot x_2 + 6 \cdot x_2^{2}\\ 213 &=& 6 \cdot x_2^{2} + 6 \cdot x_1 \cdot x_2 + 1 \cdot x_1^{2}\\ 0 &=& x_2^{2} + \frac{6}{6} \cdot x_1 \cdot x_2 + \frac{1}{6} \cdot x_1^{2} - \frac{213}{6}\\ x_{2_{1,2}}&=&-\frac{6}{2\cdot6}x_1 \pm \sqrt{\left(\frac{6}{2\cdot 6}\right)^2x_1^2-\left(\frac{1}{6} \cdot x_1^{2} - \frac{213}{6}\right)}\\ \end{aligned}\]
Wegen \(x_1 \geq 0\) und \(x_2 \geq 0\) sind wir nur an positiven Lösungen interessiert: \[\begin{aligned} x_2 = f(x_1) &=& -0.5x_1 + \sqrt{0.083333 \cdot x_1^{2} + 35.5} \end{aligned}\]
Zur Berechnung der exakten Veränderung von \(x_2\) wird die Differenz der Funktionswerte betrachtet:
\(x_1\) wird von \(9\) um \(0.3\) Einheiten auf \(9.3\) erhöht; damit muss \(x_2\) von \(f(9) = 2\) sinken auf:
\[\begin{aligned}
f(9.3) & = & -0.5 \cdot 9.3 + \sqrt{0.083333 \cdot 9.3^{2} + 35.5}\\ & = & 1.885098
\end{aligned}\] Also verändert sich \(x_2\) exakt um \(1.885098 - 2 = -0.114902 \approx -0.11\) Einheiten.
Optimierung unter Nebenbedingungen
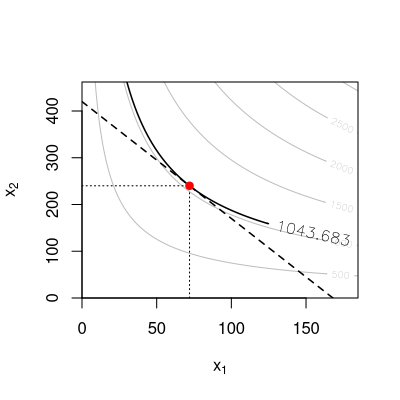
Ein Unternehmen weist folgende Produktionsfunktion auf \[F(K,L)= K L^{2}.\] Der Preis für eine Einheit Kapital beträgt \(p_K=32\) und der Preis für eine Einheit Arbeit beträgt \(p_L=28\). Minimieren Sie die Kosten des Unternehmers unter Berücksichtigung seiner Produktionsfunktion, wenn ein Output von \(260\) ME produziert werden soll.
Wie hoch ist die Menge des Inputfaktors Arbeit in diesem Kostenminimum?
1. Schritt: Problemformulierung. \[\begin{aligned} \min_{K,L} C(K,L) &=& p_KK + p_LL\\ &=& 32K + 28L\\ \mbox{unter der NB:} && F(K,L) = Q \\ && K L^{2} = 260 \end{aligned}\]
2. Schritt: Die Lagrangefunktion. \[\begin{aligned} {f}(K,L,\lambda) &=& C(K,L)-\lambda (F(K,L) - Q) \\ &=& 32K + 28L - \lambda(K L^{2} -260) \end{aligned}\]
3. Schritt: Die Bedingungen 1. Ordnung. \[\begin{aligned} \frac{\partial { {f}}}{\partial K} & = & 32 - \lambda L^{2} = 0\\ \frac{\partial { {f}}}{\partial L} & = & 28 - {2} \lambda K L^{2-1} = 0 \\ \frac{\partial { {f}}}{\partial \lambda} & = & -(K L^{2}-260) = 0 \end{aligned}\]
4. Schritt: Auflösen des Gleichungssystems nach \(K\), \(L\) und \(\lambda\).
Gleichungen (1) und (2) nach \(\lambda\) aufgelöst und gleichgesetzt ergibt: \[\begin{aligned} \frac{32}{L^{2}} & = & \frac{28}{{2} K L^{2-1}}\\ K & = & \frac{28}{2 \cdot 32} \cdot L^{2 - (2 -1)}\\ K & = & \frac{28}{64} \cdot L \end{aligned}\]
Einsetzen in die dritte Bedingung 1. Ordnung (Nebenbedingung): \[\begin{aligned} K L^{2} & = & 260\\ \left(\frac{28}{64}\cdot L \right) \cdot L^{2} & = & 260\\ \frac{28}{64} \cdot L^{3} & = & 260\\ L & = & \left(\frac{64}{28} \cdot 260\right)^{\frac{1}{3}} = 8.407466~\approx~8.41\\ % K & = & \frac{28}{64} \cdot L = 3.678266~\approx~3.68 \end{aligned}\]
Bei gegebener Produktionsfunktion ist die Menge des Inputfaktors Arbeit \(L=8.41\).
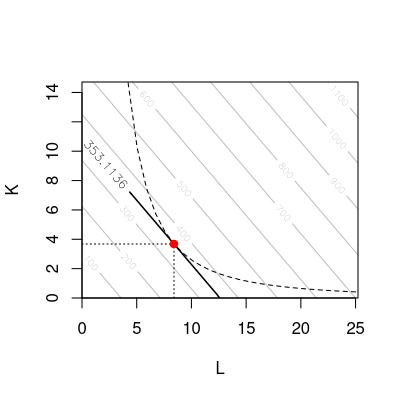
Ein Unternehmen weist folgende Produktionsfunktion auf \[F(K,L)= K L^{3}.\] Der Preis für eine Einheit Kapital beträgt \(p_K=31\) und der Preis für eine Einheit Arbeit beträgt \(p_L=35\). Minimieren Sie die Kosten des Unternehmers unter Berücksichtigung seiner Produktionsfunktion, wenn ein Output von \(120\) ME produziert werden soll.
Wie hoch ist die Menge des Inputfaktors Kapital in diesem Kostenminimum?
1. Schritt: Problemformulierung. \[\begin{aligned} \min_{K,L} C(K,L) &=& p_KK + p_LL\\ &=& 31K + 35L\\ \mbox{unter der NB:} && F(K,L) = Q \\ && K L^{3} = 120 \end{aligned}\]
2. Schritt: Die Lagrangefunktion. \[\begin{aligned} {f}(K,L,\lambda) &=& C(K,L)-\lambda (F(K,L) - Q) \\ &=& 31K + 35L - \lambda(K L^{3} -120) \end{aligned}\]
3. Schritt: Die Bedingungen 1. Ordnung. \[\begin{aligned} \frac{\partial { {f}}}{\partial K} & = & 31 - \lambda L^{3} = 0\\ \frac{\partial { {f}}}{\partial L} & = & 35 - {3} \lambda K L^{3-1} = 0 \\ \frac{\partial { {f}}}{\partial \lambda} & = & -(K L^{3}-120) = 0 \end{aligned}\]
4. Schritt: Auflösen des Gleichungssystems nach \(K\), \(L\) und \(\lambda\).
Gleichungen (1) und (2) nach \(\lambda\) aufgelöst und gleichgesetzt ergibt: \[\begin{aligned} \frac{31}{L^{3}} & = & \frac{35}{{3} K L^{3-1}}\\ K & = & \frac{35}{3 \cdot 31} \cdot L^{3 - (3 -1)}\\ K & = & \frac{35}{93} \cdot L \end{aligned}\]
Einsetzen in die dritte Bedingung 1. Ordnung (Nebenbedingung): \[\begin{aligned} K L^{3} & = & 120\\ \left(\frac{35}{93}\cdot L \right) \cdot L^{3} & = & 120\\ \frac{35}{93} \cdot L^{4} & = & 120\\ L & = & \left(\frac{93}{35} \cdot 120\right)^{\frac{1}{4}} = 4.225704~\approx~4.23\\ K & = & \frac{35}{93} \cdot L = 1.590319~\approx~1.59 \end{aligned}\]
Bei gegebener Produktionsfunktion ist die Menge des Inputfaktors Kapital \(K=1.59\).
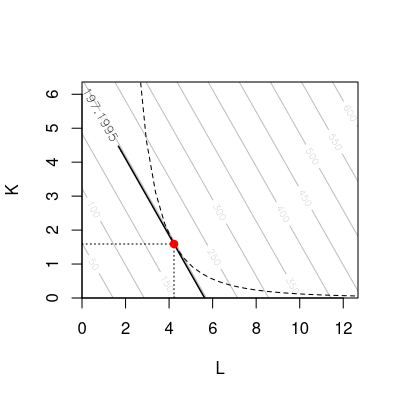
Ein Unternehmen weist folgende Produktionsfunktion auf \[F(K,L)= K L^{}.\] Der Preis für eine Einheit Kapital beträgt \(p_K=31\) und der Preis für eine Einheit Arbeit beträgt \(p_L=15\). Minimieren Sie die Kosten des Unternehmers unter Berücksichtigung seiner Produktionsfunktion, wenn ein Output von \(390\) ME produziert werden soll.
Wie hoch ist die Menge des Inputfaktors Kapital in diesem Kostenminimum?
1. Schritt: Problemformulierung. \[\begin{aligned} \min_{K,L} C(K,L) &=& p_KK + p_LL\\ &=& 31K + 15L\\ \mbox{unter der NB:} && F(K,L) = Q \\ && K L^{} = 390 \end{aligned}\]
2. Schritt: Die Lagrangefunktion. \[\begin{aligned} {f}(K,L,\lambda) &=& C(K,L)-\lambda (F(K,L) - Q) \\ &=& 31K + 15L - \lambda(K L^{} -390) \end{aligned}\]
3. Schritt: Die Bedingungen 1. Ordnung. \[\begin{aligned} \frac{\partial { {f}}}{\partial K} & = & 31 - \lambda L^{} = 0\\ \frac{\partial { {f}}}{\partial L} & = & 15 - {1} \lambda K L^{1-1} = 0 \\ \frac{\partial { {f}}}{\partial \lambda} & = & -(K L^{}-390) = 0 \end{aligned}\]
4. Schritt: Auflösen des Gleichungssystems nach \(K\), \(L\) und \(\lambda\).
Gleichungen (1) und (2) nach \(\lambda\) aufgelöst und gleichgesetzt ergibt: \[\begin{aligned} \frac{31}{L^{}} & = & \frac{15}{{1} K L^{1-1}}\\ K & = & \frac{15}{1 \cdot 31} \cdot L^{1 - (1 -1)}\\ K & = & \frac{15}{31} \cdot L \end{aligned}\]
Einsetzen in die dritte Bedingung 1. Ordnung (Nebenbedingung): \[\begin{aligned} K L^{} & = & 390\\ \left(\frac{15}{31}\cdot L \right) \cdot L^{} & = & 390\\ \frac{15}{31} \cdot L^{2} & = & 390\\ L & = & \left(\frac{31}{15} \cdot 390\right)^{\frac{1}{2}} = 28.390139~\approx~28.39\\ K & = & \frac{15}{31} \cdot L = 13.737164~\approx~13.74 \end{aligned}\]
Bei gegebener Produktionsfunktion ist die Menge des Inputfaktors Kapital \(K=13.74\).
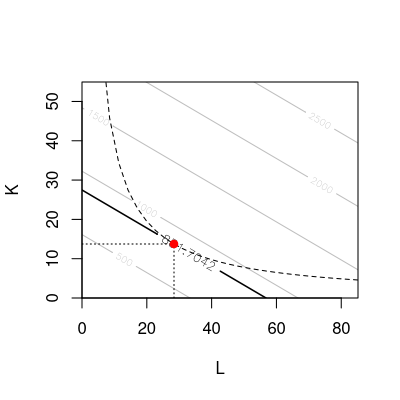
Die Produktionsfunktion eines Herstellers laute \[\begin{aligned} F(x_1,x_2) = 19 x_1^{2} + 69 x_1 x_2 + 15 x_2^{2} \end{aligned}\] Man bestimme die optimale Faktorkombination zu den Preisen \(92\) für den ersten Faktor und \(84\) für den zweiten Faktor, wenn ein Produktionsniveau von \(4549\) erzielt werden soll.
Wie hoch ist der Einsatz von Faktor \(x_2\)?
Die Lagrange-Funktion lautet \[\begin{aligned} L(x_1, x_2, \lambda) = 92 x_1 + 84 x_2 - \lambda (19 x_1^{2} + 69 x_1 x_2 + 15 x_2^{2} - 4549) \end{aligned}\] Die partiellen Ableitungen setzen wir gleich Null: \[\begin{aligned} L'_1 = 92 - \lambda (38 x_1 + 69 x_2) = 0 \\ L'_2 = 84 - \lambda (69 x_1 + 30 x_2) = 0 \\ L'_3 = -(19 x_1^{2} + 69 x_1 x_2 + 15 x_2^{2} - 4549) = 0 \\ \end{aligned}\] Die ersten beiden Gleichungen lösen wir nach \(x_1\) bzw. \(x_2\) auf \[\begin{aligned} 38x_1 + 69x_2 & = & \frac{92}{\lambda}\\ 69x_1 + 30x_2 & = & \frac{84}{\lambda} \end{aligned}\] Wir berechnen 69 \(\cdot\) \((1)\) - 38 \(\cdot\) \((2)\) um \(x_1\) und \(x_2\) in Abhängigkeit von \(\lambda\) auszudrücken \[\begin{aligned} 69 \cdot (1) : & 2622x_1 + 4761x_2 & = \frac{6348}{\lambda} \\ 38 \cdot (2) : & 2622x_1 + 1140x_2 & = \frac{3192}{\lambda} \end{aligned}\] Daraus folgt \[\begin{aligned} 3621 x_2 = \frac{3156}{\lambda} & \Longrightarrow & x_2 = \frac{3156}{3621\lambda} = \frac{0.8715824}{\lambda} \end{aligned}\] Ergebnis für \(x_2\) einsetzen in \((1)\) ergibt: \[\begin{aligned} 38x_1 + 69 \cdot \frac{3156}{3621\lambda} = \frac{92}{\lambda} & \Longrightarrow & x_1 = \frac{115368}{{137598\lambda}} = \frac{0.8384424}{\lambda} \\ \end{aligned}\] Einsetzen der Zwischenergebnisse von \(x_1\) = \(\frac{0.8384424}{\lambda}\) und \(x_2\) = \(\frac{0.8715824}{\lambda}\) in die dritte Gleichung (Nebenbedingung): \[\begin{aligned} 19 x_1^{2} + 69 x_1 x_2 + 15 x_2^{2} & = & 4549\\ 19 \cdot \frac{0.8384424^2}{\lambda^2} + 69 \cdot \frac{0.8384424 \cdot 0.8715824}{\lambda^2} + 15 \cdot \frac{0.8715824^2}{\lambda^2} & = & 4549 \Longrightarrow \lambda = \sqrt{\frac{75.174814}{4549}} = 0.128552 \end{aligned}\] Das ergibt die optimale Faktorkombination \[\begin{aligned} x_1 = \frac{0.8384424}{0.128552} = 6.52\\ x_2 = \frac{0.8715824}{0.128552} = 6.78 \end{aligned}\]
Im Optimum beträgt der Faktoreinsatz von \(x_2\) damit \(6.78\).
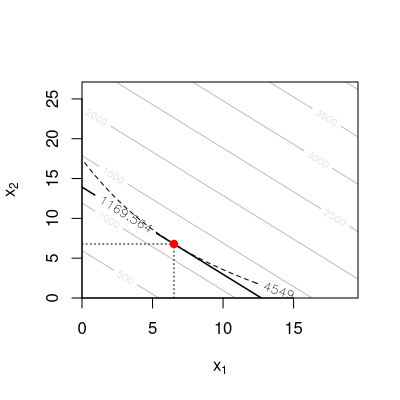
Die Produktionsfunktion eines Herstellers laute \[\begin{aligned} F(x_1,x_2) = 4 x_1^{2} + 63 x_1 x_2 + 18 x_2^{2} \end{aligned}\] Man bestimme die optimale Faktorkombination zu den Preisen \(98\) für den ersten Faktor und \(80\) für den zweiten Faktor, wenn ein Produktionsniveau von \(5801\) erzielt werden soll.
Wie hoch ist der Einsatz von Faktor \(x_1\)?
Die Lagrange-Funktion lautet \[\begin{aligned} L(x_1, x_2, \lambda) = 98 x_1 + 80 x_2 - \lambda (4 x_1^{2} + 63 x_1 x_2 + 18 x_2^{2} - 5801) \end{aligned}\] Die partiellen Ableitungen setzen wir gleich Null: \[\begin{aligned} L'_1 = 98 - \lambda (8 x_1 + 63 x_2) = 0 \\ L'_2 = 80 - \lambda (63 x_1 + 36 x_2) = 0 \\ L'_3 = -(4 x_1^{2} + 63 x_1 x_2 + 18 x_2^{2} - 5801) = 0 \\ \end{aligned}\] Die ersten beiden Gleichungen lösen wir nach \(x_1\) bzw. \(x_2\) auf \[\begin{aligned} 8x_1 + 63x_2 & = & \frac{98}{\lambda}\\ 63x_1 + 36x_2 & = & \frac{80}{\lambda} \end{aligned}\] Wir berechnen 63 \(\cdot\) \((1)\) - 8 \(\cdot\) \((2)\) um \(x_1\) und \(x_2\) in Abhängigkeit von \(\lambda\) auszudrücken \[\begin{aligned} 63 \cdot (1) : & 504x_1 + 3969x_2 & = \frac{6174}{\lambda} \\ 8 \cdot (2) : & 504x_1 + 288x_2 & = \frac{640}{\lambda} \end{aligned}\] Daraus folgt \[\begin{aligned} 3681 x_2 = \frac{5534}{\lambda} & \Longrightarrow & x_2 = \frac{5534}{3681\lambda} = \frac{1.5033958}{\lambda} \end{aligned}\] Ergebnis für \(x_2\) einsetzen in \((1)\) ergibt: \[\begin{aligned} 8x_1 + 63 \cdot \frac{5534}{3681\lambda} = \frac{98}{\lambda} & \Longrightarrow & x_1 = \frac{12096}{{29448\lambda}} = \frac{0.4107579}{\lambda} \\ \end{aligned}\] Einsetzen der Zwischenergebnisse von \(x_1\) = \(\frac{0.4107579}{\lambda}\) und \(x_2\) = \(\frac{1.5033958}{\lambda}\) in die dritte Gleichung (Nebenbedingung): \[\begin{aligned} 4 x_1^{2} + 63 x_1 x_2 + 18 x_2^{2} & = & 5801\\ 4 \cdot \frac{0.4107579^2}{\lambda^2} + 63 \cdot \frac{0.4107579 \cdot 1.5033958}{\lambda^2} + 18 \cdot \frac{1.5033958^2}{\lambda^2} & = & 5801 \Longrightarrow \lambda = \sqrt{\frac{80.262972}{5801}} = 0.117627 \end{aligned}\] Das ergibt die optimale Faktorkombination \[\begin{aligned} x_1 = \frac{0.4107579}{0.117627} = 3.49\\ x_2 = \frac{1.5033958}{0.117627} = 12.78 \end{aligned}\]
Im Optimum beträgt der Faktoreinsatz von \(x_1\) damit \(3.49\).
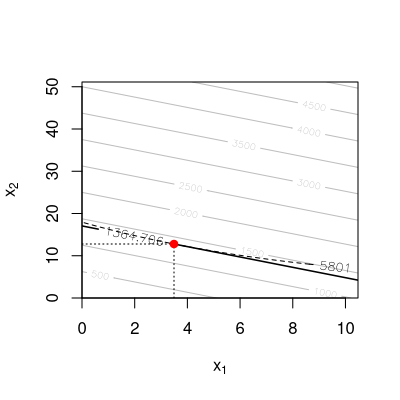
Die Produktionsfunktion eines Herstellers laute \[\begin{aligned} F(x_1,x_2) = 6 x_1^{2} + 79 x_1 x_2 + 12 x_2^{2} \end{aligned}\] Man bestimme die optimale Faktorkombination zu den Preisen \(97\) für den ersten Faktor und \(72\) für den zweiten Faktor, wenn ein Produktionsniveau von \(5435\) erzielt werden soll.
Wie hoch sind in diesem Fall die minimalen Kosten?
Die Lagrange-Funktion lautet \[\begin{aligned} L(x_1, x_2, \lambda) = 97 x_1 + 72 x_2 - \lambda (6 x_1^{2} + 79 x_1 x_2 + 12 x_2^{2} - 5435) \end{aligned}\] Die partiellen Ableitungen setzen wir gleich Null: \[\begin{aligned} L'_1 = 97 - \lambda (12 x_1 + 79 x_2) = 0 \\ L'_2 = 72 - \lambda (79 x_1 + 24 x_2) = 0 \\ L'_3 = -(6 x_1^{2} + 79 x_1 x_2 + 12 x_2^{2} - 5435) = 0 \\ \end{aligned}\] Die ersten beiden Gleichungen lösen wir nach \(x_1\) bzw. \(x_2\) auf \[\begin{aligned} 12x_1 + 79x_2 & = & \frac{97}{\lambda}\\ 79x_1 + 24x_2 & = & \frac{72}{\lambda} \end{aligned}\] Wir berechnen 79 \(\cdot\) \((1)\) - 12 \(\cdot\) \((2)\) um \(x_1\) und \(x_2\) in Abhängigkeit von \(\lambda\) auszudrücken \[\begin{aligned} 79 \cdot (1) : & 948x_1 + 6241x_2 & = \frac{7663}{\lambda} \\ 12 \cdot (2) : & 948x_1 + 288x_2 & = \frac{864}{\lambda} \end{aligned}\] Daraus folgt \[\begin{aligned} 5953 x_2 = \frac{6799}{\lambda} & \Longrightarrow & x_2 = \frac{6799}{5953\lambda} = \frac{1.1421132}{\lambda} \end{aligned}\] Ergebnis für \(x_2\) einsetzen in \((1)\) ergibt: \[\begin{aligned} 12x_1 + 79 \cdot \frac{6799}{5953\lambda} = \frac{97}{\lambda} & \Longrightarrow & x_1 = \frac{40320}{{71436\lambda}} = \frac{0.5644213}{\lambda} \\ \end{aligned}\] Einsetzen der Zwischenergebnisse von \(x_1\) = \(\frac{0.5644213}{\lambda}\) und \(x_2\) = \(\frac{1.1421132}{\lambda}\) in die dritte Gleichung (Nebenbedingung): \[\begin{aligned} 6 x_1^{2} + 79 x_1 x_2 + 12 x_2^{2} & = & 5435\\ 6 \cdot \frac{0.5644213^2}{\lambda^2} + 79 \cdot \frac{0.5644213 \cdot 1.1421132}{\lambda^2} + 12 \cdot \frac{1.1421132^2}{\lambda^2} & = & 5435 \Longrightarrow \lambda = \sqrt{\frac{68.490509}{5435}} = 0.112258 \end{aligned}\] Das ergibt die optimale Faktorkombination \[\begin{aligned} x_1 = \frac{0.5644213}{0.112258} = 5.03\\ x_2 = \frac{1.1421132}{0.112258} = 10.17 \end{aligned}\]
Die zugehörigen Kosten belaufen sich auf \[\begin{aligned} 97x_1 + 72x_2 = 97 \cdot \frac{0.5644213}{0.112258} + 72 \cdot \frac{1.1421132}{0.112258} =1220.24 \end{aligned}\] Die minimalen Kosten bei gegebener Produktionsmenge betragen \(1220.24\) Geldeinheiten.
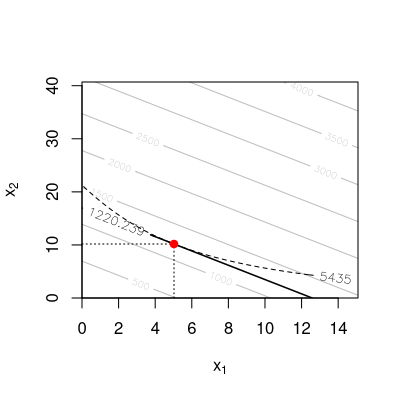
Die Nutzenfunktion eines Individuums lautet \(U(x_1,x_2)=x_1^{0.6}x_2^{0.4}\). Gegeben sind die Preise der beiden Güter \(p_1=2\) und \(p_2=1\) sowie das zur Verfügung stehende Einkommen in Höhe von \(I=750\). Optimieren Sie den Nutzen des Individuums unter Beachtung seiner Budgetrestriktion.
Wie hoch ist die Menge \(x_1\) in diesem Nutzenoptimum?
1. Schritt: Problemformulierung. \[\begin{aligned} \max_{x_1,x_2} & U(x_1,x_2) = x_1^{0.6}x_2^{0.4}\\ \mbox{unter der NB:} & {p_1}x_1 + {p_2}x_2 = I\\ & 2x_1 + 1x_2 = 750 \end{aligned}\]
2. Schritt: Die Lagrangefunktion. \[\begin{aligned} {L}(x_1,x_2,\lambda) &=& U(x_1,x_2)-\lambda({p_1}x_1 + {p_2}x_2 - I) \\ &=& x_1^{0.6}x_2^{0.4}-\lambda(2x_1 + 1x_2 - 750) \end{aligned}\]
3. Schritt: Die Bedingungen 1. Ordnung. \[\begin{aligned} \frac{\partial {L}(x_1,x_2,\lambda)}{\partial x_1} & = &0.6x_1^{0.6-1}x_2^{0.4}-2\lambda=0 \quad \Leftrightarrow \quad \frac{0.6x_1^{-0.4}x_2^{0.4}}{2}=\lambda\\ %% \frac{\partial {L}(x_1,x_2,\lambda)}{\partial x_2} & = & 0.4x_2^{0.4-1}x_1^{0.6}-1\lambda=0 \quad \Leftrightarrow \quad \frac{0.4x_2^{-0.6}x_1^{0.6}}{1}=\lambda\\ %% \frac{\partial {L}(x_1,x_2,\lambda)}{\partial \lambda} & = & -(2x_1+1x_2-750)=0 \quad \Leftrightarrow \quad 2x_1+1x_2=750 \end{aligned}\]
4. Schritt: Auflösen des Gleichungssystems.
Nach Auflösung der Gleichungen (1) und (2) nach \(\lambda\) können diese gleichgesetzt werden. Man erhält \(x_1=x_1(x_2)\) (möglich ist natürlich auch \(x_2=x_2(x_1)\)). \[\begin{aligned} \frac{0.6}{2}\left(\frac{x_2^{0.4}}{x_1^{0.4}}\right) &=&\frac{0.4}{1}\left(\frac{x_1^{0.6}}{x_2^{0.6}}\right)\\ \frac{0.6}{2} x_2 &=& \frac{0.4}{1} x_1 \\ x_1 &=& \frac{0.6}{2} \cdot \frac{1}{0.4} x_2 = 0.75 x_2 \end{aligned}\] Diese Gleichung drückt das Austauschverhältnis beider Güter im Nutzenoptimum aus (\(\frac{x_1}{x_2}~=~0.75\)). Gleichung (3) beschränkt jedoch als Budgetrestriktion diese Möglichkeiten. Die numerischen Werte für \(x_1\), \(x_2\), unter gegebener Nebenbedingung, sind die optimalen Güterkombinationen bei verfügbarem Einkommen, Preisen und individueller Nutzenfunktion.
Eingesetzt in die dritte Bedingung 1. Ordnung ergibt: \[\begin{aligned} && 2x_1 + 1x_2 = 750\\ && 2 \cdot (0.75x_2) + 1x_2 = 750\\ && ~\rightarrow~ x_2 = 300 \approx 300.00\\ && ~\rightarrow~ x_1 = 0.75 \cdot x_2 = 225 \approx 225.00 \ \end{aligned}\]
Im Nutzenoptimum bei gegebener Budgetrestriktion ist die Menge \(x_1 = 225.00\).
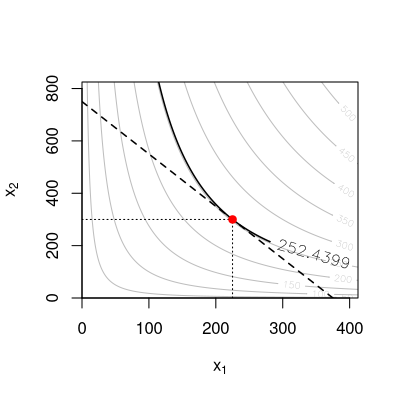
Die Nutzenfunktion eines Individuums lautet \(U(x_1,x_2)=x_1^{0.75}x_2^{0.75}\). Gegeben sind die Preise der beiden Güter \(p_1=5\) und \(p_2=1.5\) sowie das zur Verfügung stehende Einkommen in Höhe von \(I=190\). Optimieren Sie den Nutzen des Individuums unter Beachtung seiner Budgetrestriktion.
Wie hoch ist die Menge \(x_2\) in diesem Nutzenoptimum?
1. Schritt: Problemformulierung. \[\begin{aligned} \max_{x_1,x_2} & U(x_1,x_2) = x_1^{0.75}x_2^{0.75}\\ \mbox{unter der NB:} & {p_1}x_1 + {p_2}x_2 = I\\ & 5x_1 + 1.5x_2 = 190 \end{aligned}\]
2. Schritt: Die Lagrangefunktion. \[\begin{aligned} {L}(x_1,x_2,\lambda) &=& U(x_1,x_2)-\lambda({p_1}x_1 + {p_2}x_2 - I) \\ &=& x_1^{0.75}x_2^{0.75}-\lambda(5x_1 + 1.5x_2 - 190) \end{aligned}\]
3. Schritt: Die Bedingungen 1. Ordnung. \[\begin{aligned} \frac{\partial {L}(x_1,x_2,\lambda)}{\partial x_1} & = &0.75x_1^{0.75-1}x_2^{0.75}-5\lambda=0 \quad \Leftrightarrow \quad \frac{0.75x_1^{-0.25}x_2^{0.75}}{5}=\lambda\\ %% \frac{\partial {L}(x_1,x_2,\lambda)}{\partial x_2} & = & 0.75x_2^{0.75-1}x_1^{0.75}-1.5\lambda=0 \quad \Leftrightarrow \quad \frac{0.75x_2^{-0.25}x_1^{0.75}}{1.5}=\lambda\\ %% \frac{\partial {L}(x_1,x_2,\lambda)}{\partial \lambda} & = & -(5x_1+1.5x_2-190)=0 \quad \Leftrightarrow \quad 5x_1+1.5x_2=190 \end{aligned}\]
4. Schritt: Auflösen des Gleichungssystems.
Nach Auflösung der Gleichungen (1) und (2) nach \(\lambda\) können diese gleichgesetzt werden. Man erhält \(x_1=x_1(x_2)\) (möglich ist natürlich auch \(x_2=x_2(x_1)\)). \[\begin{aligned} \frac{0.75}{5}\left(\frac{x_2^{0.75}}{x_1^{0.25}}\right) &=&\frac{0.75}{1.5}\left(\frac{x_1^{0.75}}{x_2^{0.25}}\right)\\ \frac{0.75}{5} x_2 &=& \frac{0.75}{1.5} x_1 \\ x_1 &=& \frac{0.75}{5} \cdot \frac{1.5}{0.75} x_2 = 0.3 x_2 \end{aligned}\] Diese Gleichung drückt das Austauschverhältnis beider Güter im Nutzenoptimum aus (\(\frac{x_1}{x_2}~=~0.30\)). Gleichung (3) beschränkt jedoch als Budgetrestriktion diese Möglichkeiten. Die numerischen Werte für \(x_1\), \(x_2\), unter gegebener Nebenbedingung, sind die optimalen Güterkombinationen bei verfügbarem Einkommen, Preisen und individueller Nutzenfunktion.
Eingesetzt in die dritte Bedingung 1. Ordnung ergibt: \[\begin{aligned} && 5x_1 + 1.5x_2 = 190\\ && 5 \cdot (0.3x_2) + 1.5x_2 = 190\\ && ~\rightarrow~ x_2 = 63.333333 \approx 63.33\\ % && ~\rightarrow~ x_1 = 0.3 \cdot x_2 = 19 \approx 19.00 \ \end{aligned}\]
Im Nutzenoptimum bei gegebener Budgetrestriktion ist die Menge \(x_2 = 63.33\).
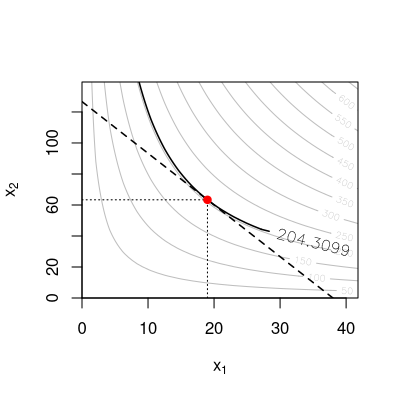
Die Nutzenfunktion eines Individuums lautet \(U(x_1,x_2)=x_1^{0.6}x_2^{0.8}\). Gegeben sind die Preise der beiden Güter \(p_1=5\) und \(p_2=2\) sowie das zur Verfügung stehende Einkommen in Höhe von \(I=840\). Optimieren Sie den Nutzen des Individuums unter Beachtung seiner Budgetrestriktion.
Wie hoch ist die Menge \(x_2\) in diesem Nutzenoptimum?
1. Schritt: Problemformulierung. \[\begin{aligned} \max_{x_1,x_2} & U(x_1,x_2) = x_1^{0.6}x_2^{0.8}\\ \mbox{unter der NB:} & {p_1}x_1 + {p_2}x_2 = I\\ & 5x_1 + 2x_2 = 840 \end{aligned}\]
2. Schritt: Die Lagrangefunktion. \[\begin{aligned} {L}(x_1,x_2,\lambda) &=& U(x_1,x_2)-\lambda({p_1}x_1 + {p_2}x_2 - I) \\ &=& x_1^{0.6}x_2^{0.8}-\lambda(5x_1 + 2x_2 - 840) \end{aligned}\]
3. Schritt: Die Bedingungen 1. Ordnung. \[\begin{aligned} \frac{\partial {L}(x_1,x_2,\lambda)}{\partial x_1} & = &0.6x_1^{0.6-1}x_2^{0.8}-5\lambda=0 \quad \Leftrightarrow \quad \frac{0.6x_1^{-0.4}x_2^{0.8}}{5}=\lambda\\ %% \frac{\partial {L}(x_1,x_2,\lambda)}{\partial x_2} & = & 0.8x_2^{0.8-1}x_1^{0.6}-2\lambda=0 \quad \Leftrightarrow \quad \frac{0.8x_2^{-0.2}x_1^{0.6}}{2}=\lambda\\ %% \frac{\partial {L}(x_1,x_2,\lambda)}{\partial \lambda} & = & -(5x_1+2x_2-840)=0 \quad \Leftrightarrow \quad 5x_1+2x_2=840 \end{aligned}\]
4. Schritt: Auflösen des Gleichungssystems.
Nach Auflösung der Gleichungen (1) und (2) nach \(\lambda\) können diese gleichgesetzt werden. Man erhält \(x_1=x_1(x_2)\) (möglich ist natürlich auch \(x_2=x_2(x_1)\)). \[\begin{aligned} \frac{0.6}{5}\left(\frac{x_2^{0.8}}{x_1^{0.4}}\right) &=&\frac{0.8}{2}\left(\frac{x_1^{0.6}}{x_2^{0.2}}\right)\\ \frac{0.6}{5} x_2 &=& \frac{0.8}{2} x_1 \\ x_1 &=& \frac{0.6}{5} \cdot \frac{2}{0.8} x_2 = 0.3 x_2 \end{aligned}\] Diese Gleichung drückt das Austauschverhältnis beider Güter im Nutzenoptimum aus (\(\frac{x_1}{x_2}~=~0.30\)). Gleichung (3) beschränkt jedoch als Budgetrestriktion diese Möglichkeiten. Die numerischen Werte für \(x_1\), \(x_2\), unter gegebener Nebenbedingung, sind die optimalen Güterkombinationen bei verfügbarem Einkommen, Preisen und individueller Nutzenfunktion.
Eingesetzt in die dritte Bedingung 1. Ordnung ergibt: \[\begin{aligned} && 5x_1 + 2x_2 = 840\\ && 5 \cdot (0.3x_2) + 2x_2 = 840\\ && ~\rightarrow~ x_2 = 240 \approx 240.00\\ % && ~\rightarrow~ x_1 = 0.3 \cdot x_2 = 72 \approx 72.00 \ \end{aligned}\]
Im Nutzenoptimum bei gegebener Budgetrestriktion ist die Menge \(x_2 = 240.00\).