2  Elementare Finanzmathematik

Die Aufgaben, die wir im Laufe dieses Kapitels lösen werden, gehören zu den einfachsten Routineaufgaben der Finanzmathematik. Man kann sie mit Hilfe von Formeln lösen, die man in Formelsammlungen nachschlagen kann, oder man verwendet Tabellen oder Computer, die für die Lösung der Aufgaben programmiert sind. Unser Ziel ist nicht, die rechnerische Fertigkeit zur Lösung dieser einfachsten finanzmathematischen Aufgaben zu vervollkommnen. Wir wollen vielmehr in der Lage sein, den Zusammenhang zwischen der ökonomischen Vorstellung von Verzinsung und ihrer mathematischen Modellierung so gut zu verstehen, dass wir in der Lage sind, die benötigten Formeln jederzeit aufzustellen und so umzuformen, wie wir sie gerade brauchen.

2.1 Verzinsungsmodelle

Wir beginnen mit der Erklärung von einigen Grundbegriffen.

Es sei \(K_0\) ein Kapital, das mit dem Zinssatz¹ \(r\) verzinst wird. Dieser bezieht sich immer auf einen bestimmten Zeitraum, die Verzinsungsperiode. Vorderhand wollen wir annehmen, dass dies ein Jahr ist, später werden wir beliebige Periodenlängen zulassen.

Der Zinssatz ist in der Regel eine Zahl \(r\) zwischen \(0\) und \(1\), also \(0\le r\le 1\). Unter besonderen ökonomischen Bedingungen können Zinssätze auch negativ oder größer als 1 sein.

Nach einer Verzinsungsperiode fallen Zinsen in der Höhe von \(K_0\cdot r\) an.

Bemerkung 2.1 (Interpretation des Zinses) Die Volkswirtschaftslehre kennt eine Reihe ökonomischer Interpretationen des Zinses. Ein sehr bekanntes und prominentes Beispiel ist die Liquiditätspräferenztheorie von John M. Keynes. Hier werden Zinsen interpretiert als Entgelt dafür, dass Wirtschaftssubjekte vorübergehend auf Liquidität verzichten. In der modernen Finanzmathematik werden Zinsen häufig als Entgelt für das Risiko betrachtet, das Gläubiger eingehen, wenn sie Schuldnern Kapital zur Verfügung stellen.

Wenn am Ende eines Jahres die Zinsen \(K_0r\) dem Anfangskapital \(K_0\) zugeschlagen werden, dann beträgt \(K_1\), das Endkapital am Ende des Jahres: \[ \begin{gathered} K_1=K_0+K_0r=K_0(1+r). \end{gathered} \] Der Faktor \(1+r\) heißt Aufzinsungsfaktor. Die Gleichung \[ \begin{gathered} K_1=K_0(1+r) \end{gathered} \tag{2.1}\] heißt Grundgleichung der Finanzmathematik und ist Basis für alle weiteren Überlegungen in Zusammenhang mit Verzinsung.

Wir stellen uns nun vor, dass nicht nur am Ende eines einzigen Jahres verzinst wird, sondern dass dies über \(t\) Jahre geschieht. Es sei \(K_1\) der Kapitalstand nach dem ersten Jahr, \(K_2\) der Kapitalstand nach dem zweiten Jahr, usw. Wir wollen ausrechnen, wie hoch der Kapitalstand \(K_t\) nach \(t\) Jahren ist.

Es gibt zwei grundsätzlich verschiedene Verzinsungsmodelle. Bei einfacher Verzinsung wird nur das Anfangskapital \(K_0\) verzinst. Bei zusammengesetzter Verzinsung (Verzinsung mit Zinseszinsen) werden auch die angefallenen Zinsen der Verzinsung unterworfen. Die beiden Verzinsungsmodelle führen zu unterschiedlichen Werten für das Endkapital. Beide Modelle spielen in der ökonomischen Praxis eine Rolle. Wir sehen uns nun die mathematische Beschreibung der beiden Verzinsungsmodelle genauer an.

2.1.1 Einfache Verzinsung

Das einfache Verzinsungsmodell ist mathematisch sehr einfach zu beschreiben, denn dabei entwickelt sich das Kapital nach folgendem linearen Schema:

\[ \begin{gathered} \begin{array}{lclcl} K_1 &=& K_0+K_0r &=& K_0(1+r) \\ K_2 &=& K_1+K_0r &=& K_0(1+2r) \\ K_3 &=& K_2+K_0r &=& K_0(1+3r)\\ \ldots\\ K_t &=& K_{t-1}+K_0r &=& K_0(1+tr). \end{array} \end{gathered} \] Aus der letzten Zeile des Schemas können wir die Beziehung zwischen dem Anfangskapital \(K_0\), dem Endkapital \(K_t\), dem Zinssatz \(r\) und der Laufzeit \(t\) ablesen: \[ \begin{gathered} K_t=K_0(1+tr). \end{gathered} \tag{2.2}\] Die Größe \(K_t\) wird Endwert genannt, \(K_0\) das Anfangskapital oder Barwert von \(K_t\). Wenn wir drei der vier Größen \(K_0\), \(K_t\), \(t\) und \(r\) kennen, dann können wir die vierte Größe berechnen. Die Kernbotschaft von (2.2) ist, dass sich bei einfacher Verzinsung der Endwert als lineare Funktion der Laufzeit \(t\) entwickelt mit einem Anstieg in der Höhe der jährlichen Zinsen, nämlich \(K_0r\).

Musteraufgabe 2.2 Ein Kapital von 2500 GE erreicht durch einfache Verzinsung nach \(12\) Perioden die Höhe von 4450 GE. Wie hoch ist der Zinssatz?

Lösung: Zur Beantwortung dieser Frage setzen wir die bekannten Größen in die Formel (2.2) ein, also \[ \begin{gathered} K_t=K_0(1+tr)=2500(1+12r) = 4450. \end{gathered} \] Diese Gleichung ist nach \(r\) aufzulösen. Einfache Umformungen ergeben \[ \begin{gathered} r=\frac{1}{t}\Big(\frac{K_t}{K_0}-1\Big) =\frac{1}{12}\Big(\frac{4450}{2500}-1\Big)=0.065. \end{gathered} \] Der Zinssatz beträgt also 6.5 Prozent. □

Das Modell der einfachen Verzinsung ist nicht auf ganze Perioden beschränkt. Es ist auch möglich, die Kapitalentwicklung für Teile von Perioden zu berechnen.

2.1.2 Zusammengesetzte Verzinsung

Einfache Verzinsung spielt wegen des linearen und damit eher langsamen Kapitalwachstums in der Praxis nur eine untergeordnete Rolle. Das in der wirtschaftlichen Praxis vorherrschende Zinsmodell ist die zusammengesetzte Verzinsung, dh. die Verzinsung mit Zinseszinsen. Bei diesem Zinsmodell entwickelt sich die Kapitalhöhe nach folgendem Schema: \[ \begin{gathered} \begin{array}{lclclcl} K_1 &=& K_0+K_0r &=& K_0(1+r) \\ K_2 &=& K_1+K_1r &=& K_1(1+r)&=&K_0(1+r)^2 \\ K_3 &=& K_2+K_2r &=& K_2(1+r)&=&K_0(1+r)^3\\ \ldots\\ K_t &=& K_{t-1}+K_{t-1}r&=&K_{t-1}(1+r) &=& K_0(1+r)^t. \end{array} \end{gathered} \] Aus der letzten Gleichung können wir wieder die Beziehung zwischen dem Anfangskapital \(K_0\), dem Endwert \(K_t\), dem Zinssatz \(r\) und der Laufzeit \(t\) ablesen: \[ \begin{gathered} K_t=K_0(1+r)^t. \end{gathered} \tag{2.3}\] Diese Gleichung wird Endwertgleichung der zusammengesetzten Verzinsung genannt. Die Größe \(1+r\) ist so wichtig, dass wir für sie einen eigenen Begriff und ein eigenes Symbol verwenden: \[ \begin{gathered} \text{Aufzinsungsfaktor:}\quad q=1+r. \end{gathered} \] Wir sehen, dass bei der mathematischen Beschreibung dieses Zinsmodells, der Endwertgleichung, Potenzen auftreten. Der Endwert \(K_t\) des Kapitals entsteht durch Multiplikation des Anfangskapitals \(K_0\) mit der \(t\)-ten Potenz des Aufzinsungsfaktors \(q^t=(1+r)^t\). Man sagt auch, der Endwert \(K_t\) ergibt sich durch Aufzinsen des Anfangskapitals über \(t\) Jahre.

Auch dieses Verzinsungsmodell kann für jede beliebige Verzinsungsdauer \(t\) verwendet werden.

Die Endwertgleichung (2.3) stellt die Beziehung zwischen den Größen \(K_0\), \(K_t\), \(t\) und \(r\) bei Verzinsung mit Zinseszinsen her. Wenn drei der Größen bekannt sind, dann ist auch die vierte Größe eindeutig bestimmt und kann berechnet werden. Die Grundgleichung ist in diesem Fall etwas komplizierter als bei einfacher Verzinsung. Wir werden uns daher genauer ansehen, wie wir jede einzelne der vier beteiligten Größen berechnen können.

Berechnung des Endwerts

Die Endwertgleichung selbst gibt an, wie der Endwert \(K_t\) des Kapitals zu berechnen ist.

Musteraufgabe 2.3 Wie hoch ist der Endwert des Kapitals \(K_0=1000\) nach 10 Jahren bei Verzinsung mit dem Zinssatz \(r=0.075\)?

Lösung: Der Endwert beträgt: \[ \begin{gathered} K_{10}=K_0(1+r)^{10}=1000(1+0.075)^{10}=2061.03. \end{gathered} \] □

Berechnung des Barwerts

Für die Berechnung des Anfangskapitals \(K_0\), des Barwerts von \(K_t\), gehen wir wieder von der Endwertgleichung (2.3) aus und erhalten durch Umformen \[ \begin{gathered} K_0=\frac{K_t}{(1+r)^t}=K_t\Big(\frac{1}{1+r}\Big)^t. \end{gathered} \tag{2.4}\] Die Größe \(1/(1+r)\) ist ebenfalls so bedeutsam, dass wir für sie einen eigenen Begriff, Diskontfaktor oder Abzinsungsfaktor, und ein eigenes Symbol, nämlich \(d\), verwenden: \[ \begin{gathered} \text{Abzinsungsfaktor:}\quad d=\frac{1}{1+r}. \end{gathered} \]

Der Barwert \(K_0\) des Kapitals \(K_t\) entsteht also durch Multiplikation des Endwerts \(K_t\) mit der \(t\)-ten Potenz \(d^t\) des Abzinsungsfaktors: \(K_0=K_td^t\). Wir sagen auch kurz: der Endwert wird über \(t\) Jahre abgezinst.

Musteraufgabe 2.4 Wie hoch ist der Barwert eines Kapitals \(K_{10}=30000\) bei einem Zinssatz \(r=0.05\)?

Lösung: Der Abzinsungsfaktor beträgt \[ \begin{gathered} d=\frac{1}{1+r}=\frac{1}{1.05}, \end{gathered} \] und daher ergibt sich ein Barwert von: \[ \begin{gathered} K_0=K_{10}d^{10}=\frac{30000}{1.05^{10}} =18417.40\,. \end{gathered} \] □

Musteraufgabe 2.5 Eine Person A sei verpflichtet, in 5 Jahren an eine Person B eine Zahlung in Höhe von 10000 GE zu leisten. Nach einem Jahr wird vereinbart, eine gleichwertige Zahlung aber sofort zu leisten. Wie hoch muss diese Zahlung sein, wenn ein Zinssatz von 8 % angenommen wird?

Lösung: Wenn A bereit ist, die Zahlung vorzeitig zu leisten, so ist der zu bezahlende Betrag der Barwert der Schuld \(K_5=10000\). Der Abzinsungsfaktor beträgt \(d=\frac{1}{1+r}=1/1.08\) und nach dem ersten Jahr verbleibt noch eine Laufzeit von 4 Jahren.

Das ergibt nach einem Jahr den Barwert \[ \begin{gathered} K_1=K_5d^4=\frac{10000}{1.08^4}=7350.30\,. \end{gathered} \] □

Das letzte Beispiel macht klar, warum der Barwert auch Gegenwartswert (present value) einer Schuld genannt wird: es ist der heutige Wert einer Schuld, die erst in Zukunft fällig wird.

Berechnung des Zinssatzes

Unsere nächste Aufgabe besteht darin, den Zinssatz \(r\) aus den übrigen Größen zu berechnen.

Mit einfachen Umformungen erhalten wir aus der Endwertgleichung (2.3) \[ \begin{gathered} \begin{array}{lcl} K_t=K_0(1+r)^t &\Rightarrow& \displaystyle\frac{K_t}{K_0}=(1+r)^t \\ &&\\ &\Rightarrow& \displaystyle 1+r=\sqrt[t]{\frac{K_t}{K_0}} =\Big(\frac{K_t}{K_0}\Big)^{1/t} \\ &&\\ &\Rightarrow& \displaystyle r=\Big(\frac{K_t}{K_0}\Big)^{1/t}-1. \end{array} \end{gathered} \] Wir sehen, dass bei der Lösung eine \(t\)-te Wurzel auftritt. Wurzeln kann man aber auch als Potenzen mit gebrochen rationalen Exponenten auffassen.

Musteraufgabe 2.6 Welcher Zinssatz ist nötig, damit sich ein Kapital innerhalb von 10 Jahren verdoppelt?

Lösung: Wenn sich das Kapital innerhalb von 10 Jahren verdoppeln soll, dann heißt das, dass \(K_{10}=2K_0\). Demnach gilt \[ \begin{gathered} K_{10}=K_0(1+r)^{10}=2K_0,\;\text{also}\; (1+r)^{10}=2. \end{gathered} \] Indem wir diese Gleichung nach \(r\) auflösen, erhalten wir den Zinssatz durch \[ \begin{gathered} r= 2^{1/10}-1=0.071773\simeq 7.18 \;\text{Prozent}. \end{gathered} \] □

Für das folgende Beispiel benötigen wir einen neuen Begriff aus der Finanzmathematik:

Definition 2.7 (Zero Bond) Unter einem Zero Bond oder einer Nullkupon-Anleihe versteht man ein Schuldpapier, bei dem während der Laufzeit weder Zinsen noch Tilgungsraten bezahlt werden. Die Zinsen einschließlich der Zinseszinsen werden erst am Ende der Laufzeit zusammen mit der Tilgung (Nominale) bezahlt.

Musteraufgabe 2.8 Jemand erwirbt einen Zero Bond zum Ausgabepreis von 80 245.10 GE, fünf Jahren Laufzeit und zugesagtem Rückzahlungswert (Nominale) von 100 000 GE. Was ist die Rendite dieses Wertpapiers?

Lösung: Rendite ist in diesem Zusammenhang nichts anderes als die Verzinsung \(r\), die mit diesem Schuldpapier erzielt wird. Die Schuld ist gleich dem Ausgabepreis (Barwert), die zugesagte Rückzahlung ist der Endwert der Schuld.

Es gilt die Endwertgleichung (2.3), die wir nach \(r\) auflösen: \[ \begin{gathered} 100000 = 80245.10\cdot (1+r)^5\implies r=\sqrt[5]{\frac{100000}{80245.10}}-1 =0.045\,. \end{gathered} \] Es wird also eine Rendite von 4.5 % erzielt. □

Musteraufgabe 2.9 Ein Unternehmen plant in 15 Jahren eine neue Produktionsanlage zu errichten. Man rechnet, dass die Errichtungskosten in 15 Jahren 30 Mio. GE betragen werden. Deshalb werden Barmittel als Rücklage bei einer Bank zu einem Zinssatz \(r\) veranlagt, die mit Zins und Zinseszins in 15 Jahren auf den Betrag von 30 Mio GE anwachsen sollen, der zur Finanzierung der Anlage ausreicht. Nach 6 Jahren jedoch senkt die Bank den Zinssatz auf 6 %. Um das geplante Ziel zu erreichen muss das Unternehmen einen Betrag von 1 438 942 GE zulegen. Wie hoch war das veranlagte Kapital, der ursprüngliche Zinssatz?

Lösung: Wir bezeichnen mit \(K_0\) die zu Beginn angelegte Summe und mit \(r\) den anfänglichen Zinssatz. Wäre alles nach Plan verlaufen, wäre also der Zinssatz nicht gesenkt worden, so gälte: \[ \begin{gathered} K_0(1+r)^{15}=30\,000\,000. \end{gathered} \] Nach 6 Jahren sinkt aber der Zinssatz auf 6 %, und die daran anschließende Entwicklung folgt der Gleichung \[ \begin{gathered} \left[K_0(1+r)^6 + 1\,438\,942\right] \cdot 1.06^9=30\,000\,000. \end{gathered} \] Dieses Gleichungssystem in den Unbekannten \(K_0\) und \(r\) müssen wir lösen. Dazu rechnen wir \(K_0\) aus der ersten Gleichung aus: \[ \begin{gathered} K_0=\frac{30\,000\,000}{(1+r)^{15}}, \end{gathered} \] und setzen das in die zweite Gleichung ein: \[ \begin{gathered} \left[\frac{30\,000\,000}{(1+r)^{15}}\,(1+r)^6 + 1\,438\,942\right] \cdot 1.06^9 = 30\,000\,000. \end{gathered} \] Wir vereinfachen: \[ \begin{gathered} \frac{30\,000\,000}{(1+r)^9}=\frac{30\,000\,000}{1.06^9}-1\,438\,942 =16\,318\,011.91\\[5pt] \frac{1}{(1+r)^9}=\frac{16\,318\,011.91}{30\,000\,000}=0.543934\\[5pt] (1+r)^9=1.838459\\[5pt] 1+r = 1.838459^{1/9}=1.07\,. \end{gathered} \] Der ursprüngliche Zinssatz betrug also \(r=0.07\). Das anfänglich veranlagte Kapital war: \[ \begin{gathered} K_0=\frac{30\,000\,000}{1.07^{15}}=10\,873\,380.59\,. \end{gathered} \] □

2.2 Laufzeiten

2.2.1 Exponentialgleichungen

Wir haben in Zusammenhang mit zusammengesetzter Verzinsung noch nicht die Aufgabe behandelt, die Laufzeit \(t\), dh. die Anzahl der Perioden aus den anderen Größen \(K_0,\,K_t,\,r\) zu berechnen.

Wenn wir aber die Laufzeit \(t\) berechnen wollen, dann müssen wir aus unserer Grundgleichung \(K_t=K_0(1+r)^t\) die Unbekannte \(t\) aus dem Exponenten herauslösen. Eine solche Gleichung heißt daher Exponentialgleichung.

Mit den Mitteln der Potenzrechnung können wir nur Gleichungen der Form \(x^p=b\) lösen. Eine solche Gleichung, bei der die unbekannte Größe \(x\) in der Basis steht, nennt man eine Potenzgleichung. Es ist dann, wie wir wissen, \(x=b^{1/p}\), sofern \(p\not=0\) und \(b>0\) ist.

Eine allgemeine Exponentialgleichung hat aber die Form \(a^x=b\). Mit Mitteln der Potenzrechnung ist es nicht möglich, eine geschlossene Formel für \(x\) anzugeben, die mit einem Taschenrechner oder Computer auswertbar wäre. Dazu brauchen wir ein neues mathematisches Konzept, nämlich den Logarithmus.

Der Logarithmus

Bekanntlich ist \(10^p\) für alle Exponenten \(p\in\mathbb R\) eine positive Zahl. Uns geht es jetzt um das umgekehrte Problem: Gibt es zu jeder positiven Zahl \(b>0\) einen Exponenten \(p\) mit der Eigenschaft \(10^p=b\)? Man kann allgemein nachweisen, dass sich diese Frage positiv beantworten lässt:

Definition 2.10 Es sei \(b>0\) eine positive Zahl. Dann heißt der Exponent \(p\in\mathbb R\) mit der Eigenschaft \(10^p=b\) der Logarithmus von \(b\) zur Basis \(10\). Man verwendet die Bezeichnung \(p=\log b\).

Es gilt die grundlegende Beziehung: \[ \begin{gathered} b=10^{\log b}. \end{gathered} \tag{2.5}\]

Wir beleuchten diese Definition durch einige Beispiele:

Weil \(1=10^0\) ist \(\log 1=0\). Außerdem: \[ \begin{aligned} %% {alignat*}{3} 10&=10^1&\quad\implies &\log 10&=1\\ 100&=10^2&\quad\implies &\log 100&=2&,\quad \text{usw.}\\ 0.1 &=10^{-1}&\quad\implies &\log 0.1&=-1\\ 0.01 &=10^{-2}&\quad\implies &\log 0.01&=-2&,\quad \text{usw.} \end{aligned} \] Für Zahlen, die keine ganzzahligen 10er-Potenzen sind, brauchen wir einen Taschenrechner. Mit dessen Hilfe finden wir beispielsweise: \[ \begin{gathered} \log 11=1.041393,\quad\log 0.75=-0.124939\,. \end{gathered} \]

Bemerkung 2.11 Zur Definition des Logarithmus sind einige zusätzliche Erklärungen nötig. Erstens erscheint es willkürlich, die Basis 10 als Grundlage für die Definition des Logarithmus zu verwenden. Ein solcher Einwand ist durchaus berechtigt. Man kann im Grunde mit jeder positiven Zahl \(a\) als Basis einen Logarithmus definieren. Für das Lösen von beliebigen Exponentialgleichungen genügt aber eine einzige solche Definition. Und es ist aus Gründen der kulturellen Tradition üblich, die Basis 10 zu verwenden (dekadische Logarithmen). Allerdings bleiben die Dinge nicht ganz so einfach. Wir werden später eine weitere Basis für die Definition eines Logarithmus heranziehen. Dies hat aber andere Gründe als das Lösen von Exponentialgleichungen.

Wie berechnet man den Logarithmus einer Zahl? Tatsächlich ist es nicht eben einfach den Logarithmus \(p\) einer Zahl \(b>0\) zu finden. Deshalb hat man die Logarithmen schon im 17. Jahrhundert für praktische Anwendungen tabelliert. Heute verwenden wir Computer zur numerischen Berechnung von Logarithmen.

Der Logarithmus besitzt mehrere charakteristische Eigenschaften, die wir als Rechengesetze formulieren können.

Satz 2.12 (Rechengesetze)  

1. Der Logarithmus der Basis 10 ist gleich 1, dh. \(\log 10 = 1\).

2. Der Logarithmus eines Produkts ist gleich der Summe der Logarithmen der Faktoren, dh. für \(a,b>0\): \[ \begin{gathered} \log(a\cdot b)=\log a+\log b \end{gathered} \tag{2.6}\]

3. Der Logarithmus eines Quotienten ist gleich der Differenz der Logarithmen von Zähler und Nenner, dh. für \(a,b>0\): \[ \begin{gathered} \log\left(\frac{a}{b}\right)=\log a-\log b \end{gathered} \tag{2.7}\]

4. Für den Logarithmus einer Potenz gilt: \[ \begin{gathered} \log a^b = b\log a \end{gathered} \tag{2.8}\]

Die Potenzregel (2.8) ist genau das Werkzeug, das wir zum Lösen der Exponentialgleichung \(a^x=b\) brauchen.

Das Lösen von Exponentialgleichungen

Nun ist es es endlich so weit. Wir wollen sehen, wie man Logarithmen anwenden kann. Unsere im Moment wichtigste Anwendung von Logarithmen besteht darin, Exponentialgleichungen zu lösen.

Eine Exponentialgleichung hat die Form \(a^x=b\) mit \(a,b>0\) und \(a\ne 1\). Sehen wir uns zunächst allgemein an, wie Exponentialgleichungen gelöst werden.

Die Gleichung wird logarithmiert, dh. auf beiden Seiten bildet man den Logarithmus. Nach Anwendung der Regel (2.8) kann man dann \(x\) ausrechnen: \[ \begin{gathered} \begin{array}{lcl} a^x=b &\Rightarrow& \log a^x=\log b \\ &&\\ &\Rightarrow& x\log a=\log b \\ &&\\ &\Rightarrow& x=\dfrac{\log b}{\log a}. \end{array} \end{gathered} \]

Beispiel 2.13

Wir wollen die Gleichung \(3^x=7\) lösen. Das ist eine Exponentialgleichung, da die Unbekannte \(x\) im Exponenten steht. Wir bilden auf beiden Seiten der Gleichung den Logarithmus: \[ \begin{gathered} \log 3^x=\log 7. \end{gathered} \] Nun kommt das Rechengesetz (2.8) zur Anwendung. Es sagt uns, dass \(\log 3^x=x\log 3\). Damit hat unsere Gleichung die Form \[ \begin{gathered} x\log 3=\log 7. \end{gathered} \] Indem wir durch \(\log 3\) dividieren, erhalten wir die Lösung \[ \begin{gathered} x=\frac{\log 7}{\log 3}=\frac{0.845098}{0.477121}=1.771244. \end{gathered} \] Dabei haben wir die Resultate auf 6 Stellen gerundet. Eine Kontrollrechnung zeigt uns: \[ \begin{gathered} 3^{1.771244}=7.000001929\simeq 7. \end{gathered} \] Als zweites numerisches Beispiel lösen wir die Exponentialgleichung \(0.99^x=0.5\). Wir bilden wieder auf beiden Seiten Logarithmen und erhalten \[ \begin{gathered} x=\frac{\log 0.5}{\log 0.99}= \frac{-0.301030}{-0.004365}=68.967564. \end{gathered} \]

2.2.2 Die Berechnung von Laufzeiten

Der Logarithmus und das Lösen von Exponentialgleichungen sind wichtige Hilfsmittel bei der Bewältigung finanzmathematischer Aufgaben. In diesem Abschnitt geht es darum, Laufzeiten von Kapitalanlagen zu berechnen.

Musteraufgabe 2.14 Wie lange müssen 1000 GE zu 5% mit Zinseszinsen angelegt bleiben, damit das Endkapital 1500 GE beträgt?

Lösung: Wenn wir die Angaben in die Grundgleichung \(K_t=K_0(1+r)^t\) einsetzen, dann erhalten wir die Exponentialgleichung \[ \begin{gathered} 1500=1000\cdot 1.05^t. \end{gathered} \] Die unbekannte Laufzeit \(t\) ist zu berechnen. Wir vereinfachen und logarithmieren: \[ \begin{gathered} 1.5=1.05^t\quad\Rightarrow\quad \log 1.5 =t\log 1.05 \quad \Rightarrow\quad t=\dfrac{\log 1.5}{\log 1.05}=8.31\,. \end{gathered} \] Die erforderliche Laufzeit beträgt also 8.31 Jahre. □

Wir sehen uns noch ein Beispiel an.

Musteraufgabe 2.15 Wie lange dauert es, bis sich das Kapital auf einem Sparbuch mit 8-prozentiger Verzinsung durch Verzinsung verdoppelt?

Lösung: Das ist eine typische Aufgabenstellung, die auf eine Exponentialgleichung führt und mit Hilfe des Logarithmus gelöst werden kann.

Es sei \(K_0\) ein Anfangskapital. Wir suchen jene Laufzeit \(t\), für die \[ \begin{gathered} K_0\cdot 1.08^t=2K_0, \implies 1.08^t=2. \end{gathered} \] Wenn wir diese Exponentialgleichung lösen, dann erhalten wir das Ergebnis \[ \begin{gathered} t=\frac{\log 2}{\log 1.08}=9.0065\simeq 9\text{ Jahre}. \end{gathered} \] □

Die Fragestellung des letzten Beispiels sehen wir uns nochmals etwas allgemeiner an.

Es sei \(K_0\) ein Anfangskapital und \(r\) ein Zinssatz. Nach welcher Zeit \(t\) erreicht das Kapital die Höhe \(aK_0\), wobei \(a>1\) den Vervielfachungsfaktor bezeichnet?

Diese Frage führt auf die Gleichung \[ \begin{gathered} K_0(1+r)^t=aK_0 \quad \text{bzw.} \quad (1+r)^t=a, \end{gathered} \] bei der \(t\) zu berechnen ist. Das ist eine Exponentialgleichung. Wir logarithmieren auf beiden Seiten und erhalten durch Umformen \[ \begin{gathered} t=\frac{\log a }{\log (1+r) }. \end{gathered} \]

Musteraufgabe 2.16 Wie lange müssen \(8663\) GE zu \(4\)% auf Zinseszinsen angelegt bleiben, damit das Endkapital, weiterhin mit \(4\)% verzinst, jährlich \(600\) GE Zinsen trägt?

Lösung: Das Endkapital \(K_t\) ergibt sich aus dem Anfangskapital durch \[ \begin{gathered} K_{t}=K_{0}\cdot (1+r)^t=8663\cdot(1+0.04)^t=8663\cdot1.04^t. \end{gathered} \] Für dieses Endkapital erhält man jährlich an Zinsen \[ \begin{gathered} K_{t}\cdot r=8663\cdot1.04^t\cdot0.04=600. \end{gathered} \] Aus dieser Exponentialgleichung können wir die Laufzeit berechnen: \[ \begin{gathered} 1.04^t=\dfrac{600}{0.04\cdot8663} \quad\Rightarrow\quad t=13.9974\,. \end{gathered} \] Das Anfangskapital muss also ungefähr \(14\) Jahre verzinst werden. □

Wir beschließen den Abschnitt mit einem etwas komplexeren Beispiel.

Musteraufgabe 2.17 Ein Zero Bond mit Nominale 500 000 GE wird zu einem Preis von 372 047 GE erworben. Der Bond wird mit 3 % pro Jahr verzinst. Was ist seine Laufzeit?

Lösung: Aus der Endwertformel folgt die Exponentialgleichung: \[ \begin{gathered} 500000=372047\cdot 1.03^t\,. \end{gathered} \] Ihre Lösung finden wir durch Logarithmieren: \[ \begin{gathered} t=\frac{\log(500000/372047)}{\log 1.03}=10\quad\text{Jahre}. \end{gathered} \] □

2.3 Geometrische Folgen

2.3.1 Folgen

Die Glieder einer arithmetischen Folge haben konstante Differenzen. Eine andere Möglichkeit, die Veränderungen zwischen aufeinander folgenden Folgengliedern anzugeben, ist die Bildung von relativen Differenzen: \[ \begin{gathered} \frac{\Delta x_n}{x_{n-1}}=\frac{x_n-x_{n-1}}{x_{n-1}}=\frac{x_n}{x_{n-1}}-1. \end{gathered} \] Die relative Differenz gibt den Unterschied zwischen \(x_n\) und \(x_{n-1}\) als Bruchteil (oder Prozentsatz) von \(x_{n-1}\) an.

Beispiel 2.18

Es sei \(x_n\) eine Folge, die die Kurswerte einer Aktie zu aufeinander folgenden Zeitpunkten enthält. Beispielsweise sei \[ \begin{gathered} x_0=100,\; x_1=120,\; x_2=125,\;x_3=115, \;x_4=120,\;x_5=130. \end{gathered} \] Für die wirtschaftliche Interpretation sind die Differenzen der Kurswerte weniger interessant. Wesentlich ist die relative Wertänderung, die man bei ökonomischen Anwendungen als Rendite bezeichnet. Die relative Wertänderung oder Rendite unserer Aktie beträgt in der ersten Periode \[ \begin{gathered} \frac{\Delta x_1}{x_0}=\frac{120-100}{100}=0.2=20\,\%, \end{gathered} \] in der zweiten Periode \[ \begin{gathered} \frac{\Delta x_2}{x_1}=\frac{125-120}{120}=0.0417=4.17\,\%, \end{gathered} \] in der dritten Periode \[ \begin{gathered} \frac{\Delta x_3}{x_2}=\frac{115-125}{125}=-0.08=-8\,\%, \end{gathered} \] usw. Die relativen Änderungen (prozentuellen Änderungen) oder Renditen sind es, die ökonomisch gesehen die wesentliche Information über die Wertänderung enthalten.

Da relative Differenzen (Renditen) für die Anwendungen im wirtschaftswissenschaftlichen Bereich wesentlich wichtiger sind als absolute Differenzen, spielen auch Folgen mit konstanten relativen Differenzen für wirtschaftliche Anwendungen eine ungleich wichtigere Rolle als arithmetische Folgen.

Definition 2.19 Eine Zahlenfolge \(x_n\) ist eine geometrische Folge, wenn die relativen Differenzen zwischen aufeinander folgenden Gliedern konstant sind.

Es sei \(x_n\) eine geometrische Folge mit konstanter relativer Differenz \[ \begin{gathered} r=\frac{x_n-x_{n-1}}{x_{n-1}}=\frac{x_n}{x_{n-1}}-1. \end{gathered} \] Offenbar ist dann auch der Quotient aufeinander folgender Glieder \[ \begin{gathered} \dfrac{x_n}{x_{n-1}}=1+r=:q \end{gathered} \] konstant. Wir hätten also genauso gut geometrische Folgen durch die Eigenschaft definieren können, dass der Quotient aufeinander folgender Glieder konstant ist.

Beispiel 2.20 (Geometrische Folgen)

Die Folge mit dem allgemeinen Glied \(x_n=1.1^n\) ist eine geometrische Folge, weil der Quotient \(x_n/x_{n-1}=1.1^n/1.1^{n-1}=1.1\) konstant ist. Es ist also \(q=1.1\) und die relative Differenz zwischen zwei aufeinander folgenden Gliedern beträgt \(r=q-1=0.1\) oder \(10\,\%\).

Die Folge mit dem allgemeinen Glied \(x_n=2^n\) ist eine geometrische Folge, weil der Quotient \(x_n/x_{n-1}=2^n/2^{n-1}=2\) konstant ist. Es ist also \(q=2\) und die relative Differenz zwischen zwei aufeinander folgenden Gliedern beträgt \(r=q-1=1\) oder \(100\,\%\). Die Folgenglieder verdoppeln ihren Wert mit jedem Schritt.

Es sei \(x_n=x_0+nd\) eine arithmetische Folge mit einer Differenz \(d\not=0\). Das ist dann keine geometrische Folge, denn die relative Differenz zwischen zwei aufeinander folgenden Gliedern beträgt \[ \begin{gathered} \frac{\Delta x_n}{x_{n-1}}=\frac{d}{x_0+(n-1)d}, \end{gathered} \] und diese ist nicht konstant, sondern verändert sich mit \(n\). Tatsächlich wird sie mit wachsendem \(n\) immer kleiner.

Die Folge mit dem allgemeinen Glied \(x_n=n^2\) ist ebenfalls keine geometrische Folge, weil der Quotient \(x_{n+1}/x_n=(n+1)^2/n^2=(1+1/n)^2\) nicht konstant ist, sondern von \(n\) abhängt.

Geometrische Folgen treten in wirtschaftlichen Anwendungen sehr häufig auf. Die meisten Formen des Sparens, der Rückzahlung von Krediten, aber auch der Versorgung durch Renten beruhen auf geometrischen Folgen.

Beispiel 2.21

Es \(K_0\) ein Kapital, das mit dem Zinssatz \(r\) verzinst wird. Die Folge der Kapitalhöhen \(K_n=K_0(1+r)^n\) ist dann eine geometrische Folge mit dem Quotienten \(q=1+r\). Der Quotient \(q=1+r\) ist zugleich der Aufzinsungsfaktor. Der Zinssatz \(r\) ist der relative Zuwachs des Kapitals: \[ \begin{gathered} K_{n+1}=K_n(1+r) \;\Rightarrow\; r=\frac{K_{n+1}-K_n}{K_n}. \end{gathered} \]

Folgenterme

Es ist auch bei geometrischen Folgen möglich, sie am Term ihres allgemeinen Gliedes zu erkennen.²

Satz 2.22 Eine Folge mit dem allgemeinen Glied \(x_n\) ist genau dann eine geometrische Folge, wenn das allgemeine Glied die Form \[ \begin{gathered} x_n=x_0q^n=x_0(1+r)^n \end{gathered} \tag{2.9}\] hat.

Begründung: Es sei \(x_n\) eine beliebige geometrische Folge mit dem Anfangswert \(x_0\) und dem Quotienten \(q\). Dann erhalten wir die Glieder der Folge nacheinander durch \[ \begin{gathered} \begin{array}{lclcl} x_1&=&&&x_0q\\ x_2&=&x_1q&=&x_0q^2\\ x_3&=&x_2q&=&x_0q^3\\ &&\ldots&&\\ x_n&=&&=&x_0q^n. \end{array} \end{gathered} \] Also hat das allgemeine Folgenglied die Form \(x_n=x_0q^n\).

Es sei nun umgekehrt \(x_n\) irgendeine Folge mit dem Term \(x_n=Aq^n\). Dann ist \(x_n/x_{n-1}=q\), also konstant. Offenbar ist \(x_0=A\) der Anfangswert der Folge und \(q\) ist der konstante Quotient zweier aufeinander folgender Glieder. □

Beispiel 2.23 (Eigenschaften von geometrischen Folgen)

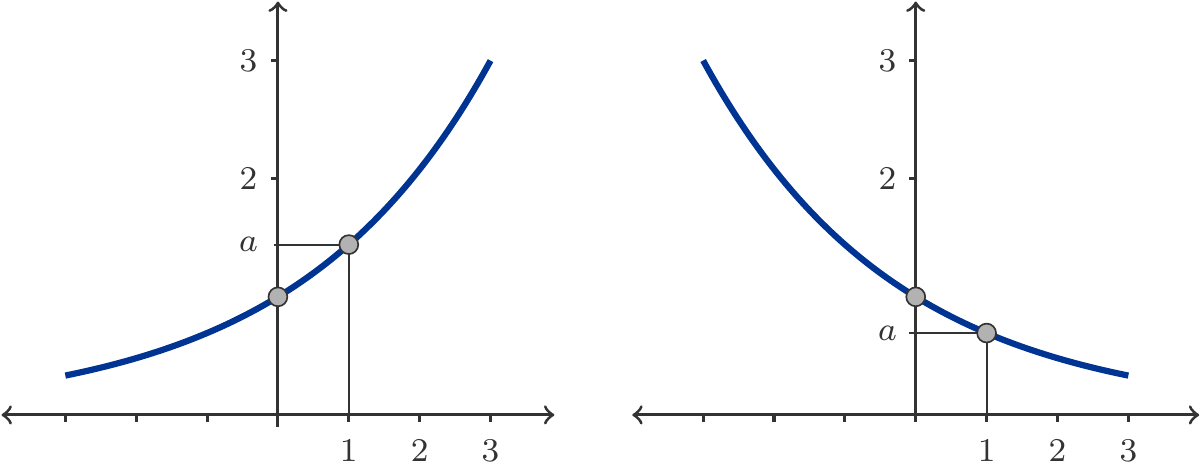
Es sei \(x_n=2\cdot1.2^n\) die geometrische Folge mit dem Anfangswert \(x_0=2\) und dem Quotienten \(q=1.2\). Die relative Differenz zweier aufeinander folgender Glieder ist \(r=q-1=0.2\), was bedeutet, dass jedes Glied um \(20\,\%\) größer ist als das vorhergehende. Also wächst die Folge streng monoton: Jedes Folgenglied ist größer als sein Vorgänger.

Es sei \(x_n=5\cdot 0.8^n\) die geometrische Folge mit dem Anfangswert \(x_0=5\) und dem Quotienten \(q=0.8\). Die relative Differenz zweier aufeinander folgender Glieder ist \(r=q-1=-0.2\), was bedeutet, dass jedes Glied um \(20\,\%\) kleiner ist als das vorhergehende. Also fällt die Folge streng monoton: Jedes Folgenglied ist kleiner als sein Vorgänger. Siehe Abbildung 2.1.

Abbildung 2.1: Die Folgen \(x_n=5\cdot 0.8^n\) und \(x_n=2\cdot 1.2^n\).

2.3.2 Summierung von Folgen

Summenformel

Wir geben sogleich eine Formel an, mit der man die Summe einer geometrischen Folge direkt berechnen kann.

Satz 2.24 (Geometrische Summenformel) Die Summe der ersten \(n\) Glieder einer geometrischen Folge beträgt, falls \(q\not=1\), \[ S_n= x_0+x_0q+x_0q^2+\cdots+x_0q^{n-1}=x_0\cdot\dfrac{q^n-1}{q-1}. \tag{2.10}\]

Begründung: Subtrahiert man die Gleichungen \[ \begin{gathered} \begin{array}{lclclclclcl} S_n &=& x_0 &+& x_0q &+& x_0q^2& + & \ldots & + & x_0q^{n-1}\\ qS_n &=& x_0q &+& x_0q^2 &+& x_0q^3& + & \ldots & + & x_0q^{n}\\ \end{array}, \end{gathered} \] so erhält man \[ \begin{gathered} S_n-qS_n=x_0-x_0q^n\implies S_n(1-q)=x_0(1-q^n), \end{gathered} \] woraus die Formel für die Partialsummen folgt. □

Beispiel 2.25

Die geometrische Folge \(x_n=(\frac{1}{2})^{n}\) hat den Anfangswert \(x_0=1\) und den Quotienten \(q=\frac{1}{2}\). Daraus folgt für die Partialsummen \[ \begin{gathered} S_n=\frac{ 1-(\frac{1}{2})^n}{1-\frac{1}{2}} =2-\Big(\frac{1}{2}\Big)^{n-1}. \end{gathered} \]

Anwendungen

Mit finanzmathematischen Anwendungen von geometrischen Summen beschäftigen wir uns im nächsten Abschnitt. Daher beschränken wir uns hier auf andere Beispiele.

Unser erstes Anwendungsbeispiel beruht auf einer berühmten Legende.

Beispiel 2.26

Der Erfinder des Schachspiels, Sissa ibn Dahir, erbat sich vom indischen König Shihram als Belohnung die Menge an Weizenkörnern, die man insgesamt erhält, wenn auf das erste Feld des Schachbretts ein Weizenkorn und auf das jeweils nächste Feld die doppelte Anzahl von Weizenkörnern gelegt werden. Wieviele Weizenkörner ergibt dies?

Es sei \(x_n\) die Anzahl der Weizenkörner, die auf dem \(n\)-ten Feld des Schachbretts zu liegen kommt. Die Folge \(x_n\) ist eine geometrische Folge mit dem Anfangsglied \(x_0=1\) und wegen der geforderten Verdopplung mit dem Quotienten \(q=2\). Also beträgt die Summe der 64 Folgenglieder \[ \begin{gathered} S_{64}= x_0\frac{q^{64}-1}{q-1}=2^{64}-1. \end{gathered} \] Wenn man diese Zahl exakt ausrechnet, dann erhält man \[ \begin{gathered} S_{64}=18\; 446\; 744\; 073\; 709\; 551\; 615 \;\approx\; 18\,447\cdot 10^{15}. \end{gathered} \] Um uns unter dieser Menge von Weizenkörner etwas vorstellen zu können, rechnen wir ihr Volumen aus.

Ein Kubikmeter enthält ungefähr 16 Millionen Weizenkörner, das sind \(1.6\cdot 10^{7}\) Weizenkörner. Daher hat unsere Menge von Weizenkörnern ein Volumen von \[ \begin{gathered} V=\frac{18\,447\cdot 10^{15}}{1.6\cdot 10^{7}}\approx11\,529\cdot 10^{8}\, \approx 1.2\cdot 10^{12}\,m^3. \end{gathered} \] Ein Kubikkilometer enthält \(1000^3=10^9\) Kubikmeter. Daher beträgt \(V=1.2\cdot 10^{3}=1\,200\) Kubikkilometer. Das entspricht einem Würfel mit einer Kantenlänge von mehr als 10 Kilometern.

Musteraufgabe 2.27 Die Bevölkerung einer Stadt wächst im ersten Jahr von 15 000 auf 15 600. Dies entspricht einer Wachstumsrate von \(600/15\,000=0.04=4\,\%\). Jeder Einwohner produziert pro Jahr \(1\,m^3\) Müll. Dieser Müll wird auf eine Deponie verbracht, die gegenwärtig Raum für 1 Million \(m^3\) hat. Wie entwickeln sich die jährlich anfallende und die gesamte deponierte Müllmenge? Wie lange reicht der Deponieraum aus?

Lösung: Um die im Laufe eines Jahres anfallende Müllmenge zu berechnen, benötigen wir die durchschnittliche Bevölkerungszahl eines Jahres. Wir nehmen der Einfachheit halber an, dass die durchschnittliche Bevölkerungszahl im ersten Jahr \(15\,300=\frac{1}{2}(15000+15600)\) beträgt³. Die im ersten Jahr anfallende Müllmenge beträgt also \(15\,300 \;m^3\). Da die Bevölkerungszahl jedes Jahr um 4 Prozent wächst, gilt das Gleiche auch für die anfallende Müllmenge. Sie bildet eine geometrische Folge mit dem Quotienten \(q=1.04\). Somit beträgt die gesamte Müllmenge nach \(n\) Jahren \[ \begin{gathered} S_n=15\,300\,\frac{1.04^n-1}{1.04-1}. \end{gathered} \] Die Deponie muss geschlossen werden, wenn \(S_n=1\,000\,000.\) Es ist also die Gleichung \[ \begin{gathered} 1\,000\,000=15\,300\,\frac{1.04^n-1}{1.04-1} \end{gathered} \] nach \(n\) aufzulösen. Dies führt auf die Exponentialgleichung \[ \begin{gathered} 1.04^n=1+0.04\,\frac{1\,000\,000}{15\,300}, \end{gathered} \] die wir mit dem Logarithmus lösen können. Die Lösung ergibt \(n=32.7613\). Die Deponie muss nach ca. 33 Jahren geschlossen werden. □

2.4 Finanzmathematische Renten

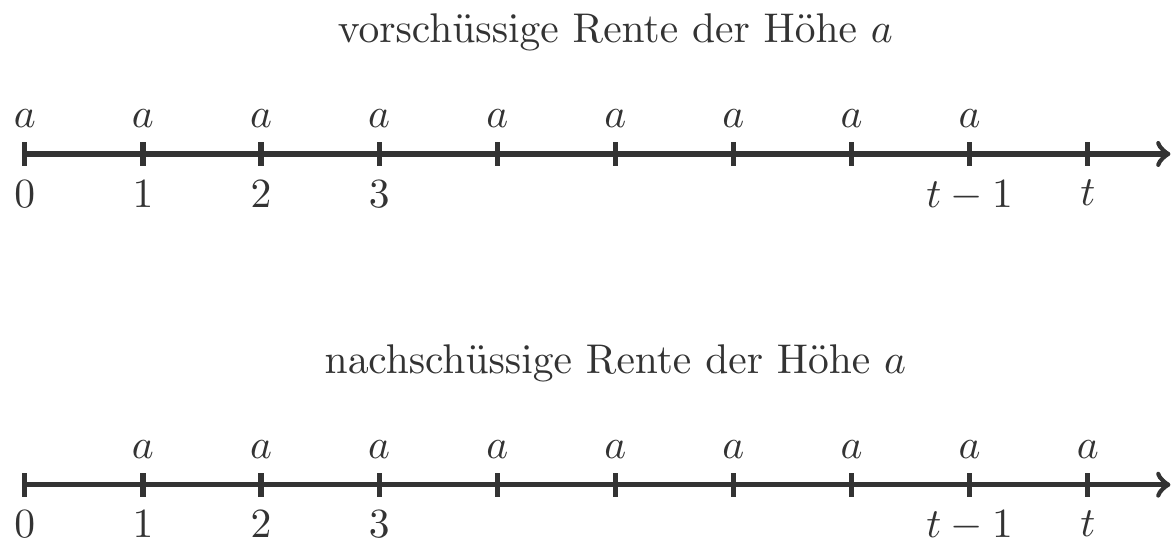
In der Finanzmathematik treten geometrische Reihen, so nennen wir Summen über geometrische Folgen, vor allem in Zusammenhang mit Renten auf. Eine Rente ist eine periodische Folge von Zahlungen, die in der Regel gleich hoch sind. Werden die Zahlungen jeweils zu Beginn einer Periode geleistet, so spricht man von einer vorschüssigen Rente. Werden sie immer am Ende einer Periode geleistet, dann ist die Rente nachschüssig. Abbildung 2.2 zeigt schematisch den Unterschied zwischen vorschüssigen und nachschüssigen Rentenzahlungen der Höhe \(a\).

Abbildung 2.2: Zeitliche Zuordnung von Rentenzahlungen.

Eine finanzmathematische Rente entspricht einem Zahlungsstrom, und es wird unsere nächste Aufgabe sein, solche Zahlungsströme unter Berücksichtigung der Verzinsung zu bewerten. Folgende Fragen werden dabei zu beantworten sein:

• Welches Kapital bildet sich im Laufe der Zeit (Kapitalaufbau)?

• Welches Kapital ist erforderlich, um über eine gewisse Zeit die Zahlungen leisten zu können (Kapitalverrentung).

Dieses Bewertungsproblem ist schwieriger zu lösen als jene Bewertungsaufgaben, die wir in diesem Kapitel bisher behandelt haben, denn die Zahlungen \(a\) erfolgen ja zu unterschiedlichen Zeitpunkten.

In der Finanzmathematik begründet man die Lösung des Bewertungsproblems auf einem einfachen Prinzip.

Äquivalenzprinzip der Finanzmathematik

Um Zahlungen, die zu unterschiedlichen Zeitpunkten erfolgen, vergleichbar zu machen, werden sie auf den gleichen Zeitpunkt \(T\) bezogen.

Die Wahl von \(T\) ist dabei unerheblich.

Ein Blick auf Abbildung 2.2 zeigt, dass zwei Zeitpunkte besonders interessant sind:

• \(T=0\): Die Zahlungen \(a\) liegen in der Zukunft, die Bewertung erfolgt vor Fälligkeit der Zahlungen. Ihr Gegenwartswert, d.h. ihr Barwert ergibt sich daher durch Abzinsen.

• \(T=t\): Die Zahlungen \(a\) erfolgen vor \(T\), die Bewertung erfolgt nach ihrer Fälligkeit, ihr Endwert ergibt sich somit durch Aufzinsen.

Barwert einer vorschüssigen Rente

Wir behandeln zuerst den Fall \(T=0\), wobei die Zahlungen \(a\) vorschüssig erfolgen sollen.

Die erste Zahlung \(a\) erfolgt zum Zeitpunkt \(0\) und hat daher den Barwert \(a\). Die zweite Zahlung erfolgt zum Zeitpunkt \(1\) und ihr Barwert ist \(ad\), siehe Abbildung 2.3. Die letzte Zahlung erfolgt zum Zeitpunkt \(t-1\), ihr Barwert ist \(ad^{t-1}\).

Abbildung 2.3: Der Barwert einer vorschüssigen Rente.

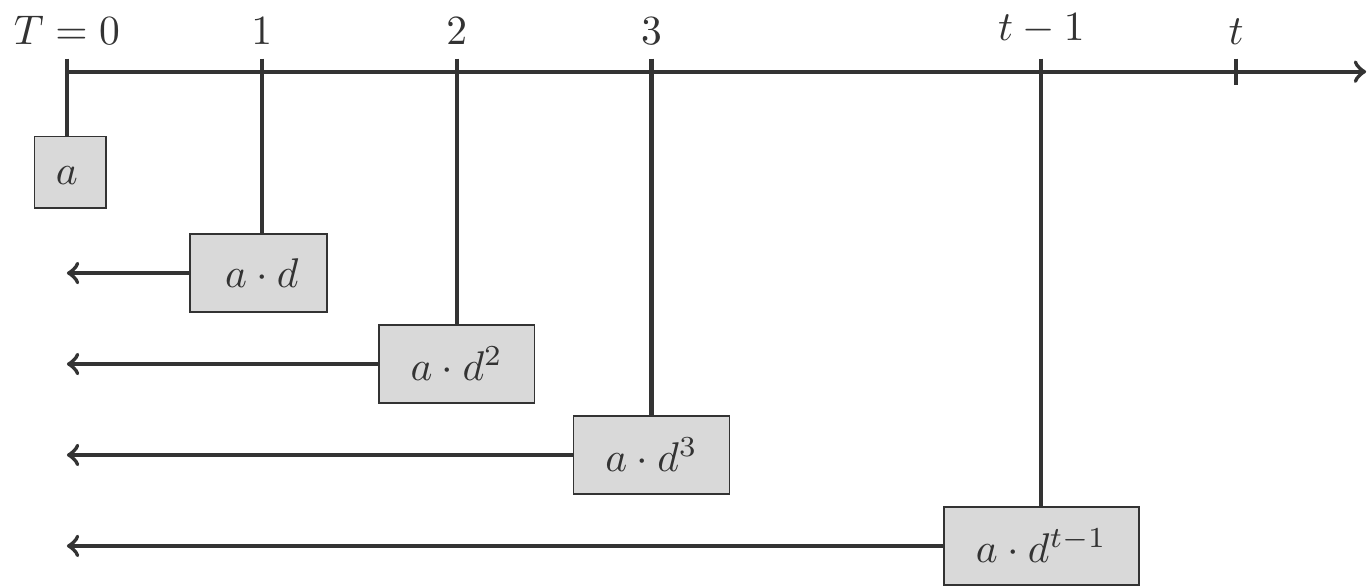
Die Barwerte aller \(t\) Zahlungen betragen also \[ \begin{gathered} a,\;ad,\;ad^2,\;ad^3,\ldots,\;ad^{t-1}, \end{gathered} \] und bilden eine geometrische Folge. Die Summe dieser Barwerte nennt man den Barwert einer vorschüssigen Rente \[ \begin{gathered} \begin{array}{lcl} B_t& =&a+ad+ad^2+ad^3+\cdots+ad^{t-1}\\[5pt] &=& a(1+d+d^2+d^3+\cdots+d^{t-1})\\[5pt] &=& a\,\dfrac{1-d^t}{1-d}. \end{array} \end{gathered} \tag{2.11}\] Der Barwert einer vorschüssigen Rente ist also bis auf den Faktor \(a\), der die Rentenhöhe angibt, einfach die Partialsumme einer geometrischen Reihe mit dem Quotienten \(d\), die wir mit Hilfe von Satz 2.24 berechnen.

Barwert einer nachschüssigen Rente

Bei einer nachschüssigen Rente berechnet man den Barwert ganz ähnlich. Der Unterschied besteht lediglich darin, dass die Zahlungen jeweils eine Periode später erfolgen. Zur Bestimmung ihres Barwerts müssen diese daher um eine Periode öfter abgezinst werden. Damit ist der Barwert einer nachschüssigen Rente: \[ \begin{gathered} \begin{array}{lcl} B_t& =&ad+ad^2+ad^3+ad^4+\cdots+ad^{t}\\[5pt] &=& ad(1+d+d^2+d^3+\cdots+d^{t-1})\\[5pt] &=& ad\,\dfrac{1-d^t}{1-d}. \end{array} \end{gathered} \tag{2.12}\]

Endwert einer vorschüssigen Rente

Nun untersuchen wir den Bewertungszeitpunkt \(T=t\), und beginnen wieder mit dem Fall, dass die Zahlungen vorschüssig erfolgen.

Abbildung 2.4: Der Endwert einer vorschüssigen Rente.

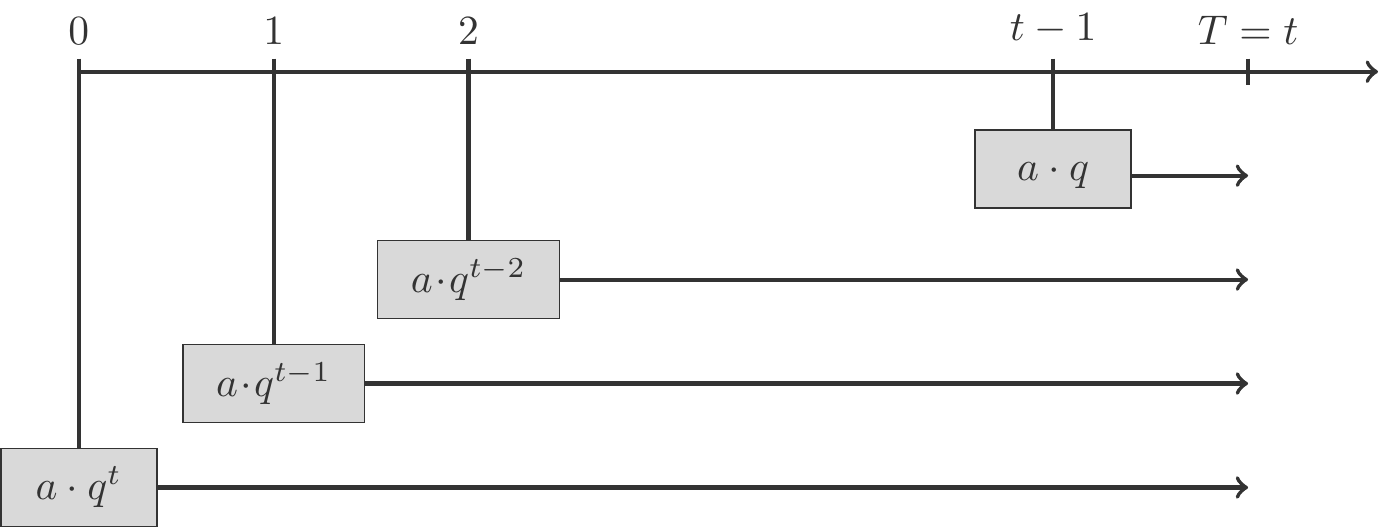
Die erste Zahlung \(a\) erfolgt zum Zeitpunkt \(0\) und hat daher den Endwert \(aq^t\). Die zweite Zahlung erfolgt zum Zeitpunkt \(1\) und ihr Endwert ist \(aq^{t-1}\). Die letzte Zahlung erfolgt zum Zeitpunkt \(t-1\). Diese muss noch eine Periode verzinst werden, denn das Rechtsgeschäft, auf dem die Zahlungsverpflichtung bzw. der Zahlungsanspruch gründet, endet erst zum Zeitpunkt \(t\). Ihr Endwert ist also \(aq\), siehe Abbildung 2.4. Die Endwerte aller \(t\) Zahlungen betragen \[ \begin{gathered} aq^t,\;aq^{t-1},\;aq^{t-2},\;aq^{t-3},\ldots,\;aq. \end{gathered} \] Die Summe dieser Endwerte der Einzelzahlungen ist der Endwert der Rente \[ \begin{gathered} \begin{array}{lcl} E_t& =&aq^t+aq^{t-1}+aq^{t-2}+aq^{t-3}+\cdots+aq\\[5pt] &=& aq(q^{t-1}+q^{t-2}+q^{t-3}+\cdots+1)\\[5pt] &=& aq\,\dfrac{q^t-1}{q-1}. \end{array} \end{gathered} \tag{2.13}\] Der Endwert einer vorschüssigen Rente ist also bis auf den Faktor \(aq\) die Partialsumme einer geometrischen Reihe mit dem Quotienten \(q\).

Nur wenig ändert sich, wenn die Zahlungen nachschüssig geleistet werden: jede Zahlung wird eine Periode weniger oft aufgezinst. Der Endwert einer nachschüssigen Rente ist damit: \[ \begin{gathered} \begin{array}{lcl} E_t& =&aq^{t-1}+aq^{t-2}+aq^{t-3}+aq^{t-4}+\cdots+a\\[5pt] &=& a(q^{t-1}+q^{t-2}+q^{t-3}+\cdots+1)\\[5pt] &=& a\,\dfrac{q^t-1}{q-1}. \end{array} \end{gathered} \tag{2.14}\]

Zusammenhang zwischen Barwert und Endwert

Es gibt aber auch noch eine andere Methode, diese Endwerte zu bestimmen. Der Barwert und der Endwert sind ja Bewertungen ein und derselben Leistung zu verschiedenen Zeitpunkten. Diese Äquivalenz muss notwendigerweise zur Folge haben, dass der Endwert der Rente identisch ist mit dem Endwert von \(B_t\), also \[ \begin{gathered} E_t=B_tq^t. \end{gathered} \tag{2.15}\] In (2.15) sind \(B_t\) und \(E_t\) beide vorschüssig oder beide nachschüssig.

Diese Gleichung haben wir auf Grund unseres Verständnisses für die Bedeutung der dahinter liegenden Begriffe gewonnen. Unseren Formeln (2.11) und (2.13) für die vorschüssige Rente kann man die Gültigkeit der Gleichung (2.15) nicht auf den ersten Blick ansehen. Aber wir können uns auf rechnerischem Weg davon überzeugen. Dabei machen wir von der Tatsache \(d=1/q\) Gebrauch. Wir sehen so, dass im vorschüssigen Fall \[ \begin{gathered} B_tq^t=a\,\frac{1-d^t}{1-d}q^t= a\,\frac{(1-1/q^t)q^t}{1-1/q}=a\,\frac{q^t-1}{1-1/q}=aq\,\frac{q^t-1}{q-1}=E_t. \end{gathered} \] Also führen uns beide Wege zum gleichen Endwert einer vorschüssigen Rente. Analoges lässt sich natürlich zeigen für die Beziehung zwischen dem nachschüssigen Barwert und Endwert.

2.4.1 Anwendungen

Musteraufgabe 2.28 Eine Versicherungsgesellschaft bietet eine Gebäudeversicherung für Einfamilienhäuser an. Bei einem Versicherungswert (Deckungssumme) von 300 000 GE beträgt die Jahresprämie, die immer am Ende des Jahres zu entrichten ist, 10 100 GE. Wieviele Jahre dauert es, bis für einen bestimmten Versicherungsnehmer die zugesagte Schadenersatzleistung von 300 000 GE durch die eingegangenen Prämienzahlungen und deren Zinsen (Zinssatz 4 %) gedeckt ist?

Lösung: Die Prämienzahlungen des Versicherten stellen eine finanzmathematische Rente mit Zahlung \(a=10100\) dar. Diese Rente ist nachschüssig, denn die Zahlungen erfolgen am Jahresende; verzinst wird mit einem Zinssatz von \(r=0.04\).

Uns interessiert es, wie lange es dauert, bis die eingegangenen Prämienzahlungen einschließlich Zins und Zinseszins die zugesagte Deckungssumme 300 000 erreicht haben. Daher interpretieren wir diese Deckungssumme als Endwert der Rente!

Wir verwenden Formel (2.14) und lösen diese zunächst nach \(q^t\) auf: \[ \begin{gathered} E=a\,\frac{q^t-1}{q-1}\implies q^t=\frac{E(q-1)}{a}+1\,. \end{gathered} \] Nun setzen wir die numerischen Angaben ein und lösen die Exponentialgleichung durch Logarithmieren: \[ \begin{gathered} 1.04^t=\frac{300000\cdot 0.04}{10100}+1=2.188119\\[4pt] t=\frac{\log(2.188119)}{\log(1.04)}=19.965\simeq 20\,. \end{gathered} \] Nach ziemlich genau \(20\) Jahren ist das versicherte Kapital gedeckt. □

Musteraufgabe 2.29 Das Management eines Unternehmens steht vor der Entscheidung, eine neue Produktionsanlage anzuschaffen. Der Preis der Anlage beträgt 400 000 GE, sie hat eine erwartete Nutzungsdauer von 10 Jahren. Wenn die Anlage in Betrieb genommen wird, generiert sie einen Netto-Cashflow von 75 000 GE pro Jahr.

Ist diese Investition bei gegebenen Eckdaten ökonomisch argumentierbar? Nehmen Sie für die Rechnung an, dass der Netto-Cashflow als Einzahlung dem Unternehmen jeweils am Jahresende zufließt und berücksichtigen Sie einen Kalkulationszinssatz von 5%.

Lösung: Wir berechnen den nachschüssigen Barwert der Netto-Cashflows mittels der Formel (2.12). Dabei setzen wir \[ \begin{gathered} d=\frac{1}{1.05},\quad a=75000,\quad t=10\,; \end{gathered} \] Die Rechnung ergibt: \[ \begin{gathered} B=ad\,\frac{1-d^{10}}{1-d}\simeq 579130\,. \end{gathered} \] Wenn nun \(I=400000\) die Investitionssumme ist, so bezeichnet die Differenz \[ \begin{gathered} B-I=579130-400000 = 179130 \end{gathered} \] den Kapitalwert der Investition. Ist dieser positiv, wie in unserem Beispiel, so ist die ins Auge gefasste Investition ökonomisch plausibel, denn der durch sie generierte Zahlungsstrom hat einen Gegenwartswert (Barwert), der höher ist als die Auszahlung, die für die Anschaffung der Anlage erforderlich ist. □

Musteraufgabe 2.30 Jemand bietet ein Haus zu einem Preis von 420000 GE zum Verkauf an. Ein Kaufinteressent bietet an, diesen Betrag in fünf gleichen Jahresraten \(a\) zu erstatten, wobei die erste Rate sofort bezahlt wird, die weiteren jeweils am Beginn der Folgejahre. Wie hoch muss die Jahresrate \(a\) sein, wenn der Rechnung ein Zinssatz von 3 % zugrunde gelegt wird?

Lösung: Das Kaufangebot stellt eine vorschüssige Rente mit unbekannter Zahlung \(a\) und fünf Jahren Laufzeit dar. Der Barwert dieser Rente muss gleich sein dem Preis, zu dem das Haus angeboten wird. Wir verwenden daher Formel (2.11) für den vorschüssigen Barwert und lösen nach \(a\): \[ \begin{gathered} B_t = a\frac{1-d^t}{1-d}\implies a = \frac{B(1-d)}{1-d^t}. \end{gathered} \] Durch Einsetzen der Daten aus der Angabe erhalten wir: \[ \begin{gathered} a=\frac{420000(1-1/1.03)}{1-1/1.03^5} = 89037.7864\simeq 89038\,. \end{gathered} \] □

Musteraufgabe 2.31 Eine \(35\)-jährige Angestellte möchte durch jährlich gleichbleibende Zahlungen von \(50\,000\) GE, die sie stets am Jahresende tätigt, bis zu ihrer Pensionierung in \(25\) Jahren einen Betrag ansparen, der ihr ab dann \(20\) Jahre lang, jeweils zu Jahresbeginn als Zusatzpension ausbezahlt werden soll. Wie hoch ist die jährliche Höhe der zu erwartenden Zusatzpension, wenn eine Verzinsung von 5 % angenommen wird?

Lösung: In dieser Aufgabe haben wir es mit zwei Zahlungsströmen zu tun:

1. Der Ansparvorgang (Kapitalaufbau): dieser stellt eine nachschüssige Rente mit 25 Jahren Laufzeit dar. Der Endwert dieser Rente ist das durch diesen Zahlungsstrom gebildete Kapital.

2. Die Zusatzpension (Kapitalverrentung): dieser Zahlungsstrom entsteht durch den Verbrauch des im Ansparvorgang gebildeten Rentenkapitals. Er entspricht einer vorschüssigen Rente mit Laufzeit 20 Jahre.

Der Endwert der Einzahlungen muss gleich sein dem Barwert der Auszahlungen. Es sei \(R\) die gesuchte Höhe der Zusatzpension, \(a=50000\), \(q=1.05\) und \(d=1/1.05\) bezeichnen wie immer Auf- und Abzinsungsfaktor. Mit den Rentenformeln (2.11) und (2.14) erhalten wir: \[ \begin{gathered} a\frac{q^{25}-1}{q-1}=R\frac{1-d^{20}}{1-d}\implies R=a\frac{q^{25}-1}{q-1}\cdot\frac{1-d}{1-d^{20}}= 182368.8518\,. \end{gathered} \] Die erwartete Höhe der jährlichen Zusatzpension beträgt somit ca. 182 369 GE, das ist mehr als das 3.6-fache des jährlichen Ansparbetrages! Die Ursache für die beeindruckende Höhe der Zusatzpension ist keineswegs die kürzere Laufzeit der Altersrente. Wenn wir die Rechnung wiederholen mit einer Laufzeit von 25 Jahren für die Altersrente, ergibt sich: \[ \begin{gathered} R'=a\frac{q^{25}-1}{q-1}\cdot\frac{1-d}{1-d^{25}}=161254.9972, \end{gathered} \] das ist immer noch mehr als das 3.2-fache des jährlichen Ansparbetrags. Dieser beeindruckende Effekt findet seine Erklärung im exponentiellen Wachstum von Kapital, das mit Zinseszinsen veranlagt wird. □

Beispiel 2.32 (Preise von Anleihen, Plain Vanilla Bonds)

Eine Standardanleihe, Plain Vanilla Bond, ist ein festverzinsliches Wertpapier, das von Staaten oder größeren Unternehmen begeben wird, um Finanzmittel am Kapitalmarkt aufzunehmen. Die Emittenten (Schuldner) garantieren den Zeichnern (Gläubigern) die Rückzahlung eines Nennwertes (Nominales) \(N\) nach \(T\) Jahren sowie während der Laufzeit fixe Zinszahlungen, Kupons \(K\), die nachschüssig einmal oder mehrmals jährlich ausbezahlt werden. Dadurch wird ein Zahlungsstrom generiert, dessen Struktur in Abbildung 2.5 dargestellt ist.

Abbildung 2.5: Zahlungsstrom einer 5-jährigen Anleihe.

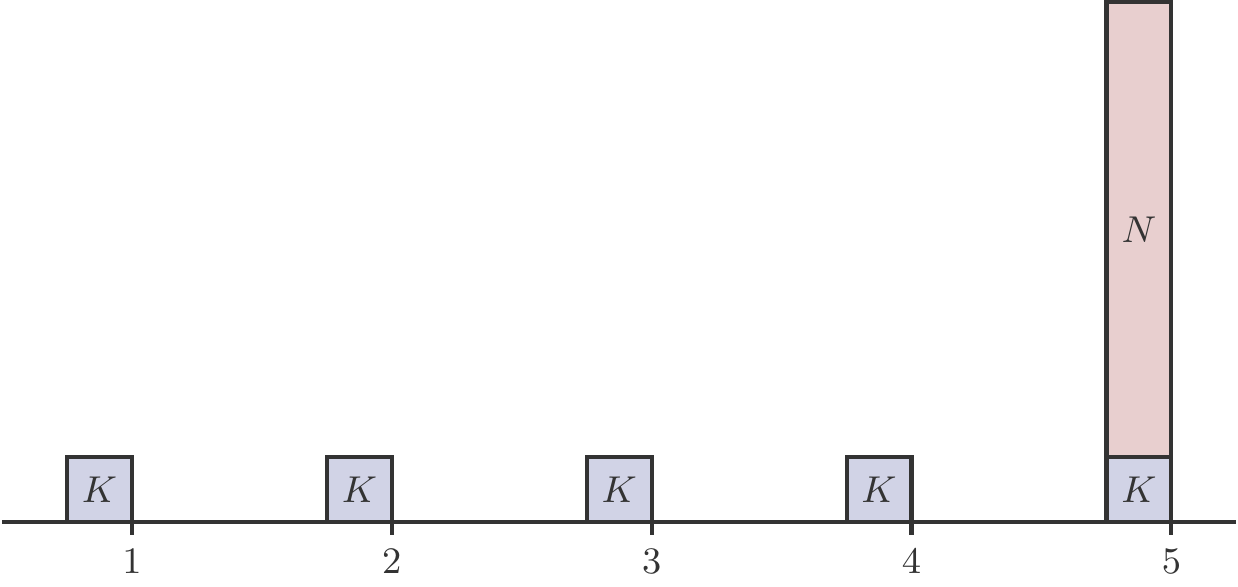
Der Preis \(P\) der Anleihe ist der Barwert dieses Zahlungsstroms. Dieser wird in der Regel in Prozent des Nominales angegeben, eine Größe, die als Kurs der Anleihe bezeichnet wird. Wir errechnen den Preis \(P\) mittels der nachschüssigen Barwertformel (2.12): \[ \begin{aligned} P &= Kd+Kd^2+\ldots+Kd^T+Nd^T\\ &=Kd\frac{1-d^T}{1-d}+Nd^T\,. \end{aligned} \tag{2.16}\]

Wir wollen nun eine konkrete Berechnung durchführen.

Musteraufgabe 2.33 Im März 2009 begab die Republik Österreich eine Anleihe mit folgenden Eckdaten:

\[ \begin{gathered} \begin{array}{ll} \text{Bundesanleihe 2009-2026/2/144A} \\ \text{ISIN AT 000A0DXC2} \\ \hline \text{Nominale} & 1000 \\ \text{Kupon} & 4.85\: \% \: \text{des Nominales jährlich} \\ \text{Laufzeit}& 17\:\text{Jahre}\\ \end{array} \end{gathered} \]

Zum Zeitpunkt der Ausgabe (März 2009) betrug der langfristige Zinssatz 3.94 %. Was war der Preis dieser Anleihe?

Lösung: Der Kupon \(K\) errechnet sich aus dem Nominale \(N=1000\) und dem zugesagten Zins: \[ \begin{gathered} K=0.0485\cdot 1000 = 48.5\,. \end{gathered} \] Abgezinst wird mit dem langfristigen Zinssatz \(r=0.0394\), daher ist \(d=1/1.0394\). Mittels (2.16) finden wir den Preis: \[ \begin{gathered} P=48.5\cdot d\cdot\frac{1-d^{17}}{1-d}+1000\cdot d^{17} = 1111.22 \end{gathered} \] Dies ergibt einen Kurs von \(P/N=1.111\), also 111.1 %. Man sagt auch, die Anleihe notierte über pari.

Was, wenn der Kuponzinssatz gleich dem Marktzins gewesen wäre?

Nun beträgt der Kupon \(Nr\). Da aber \(d=1/(1+r)\), folgt, dass \[ \begin{gathered} r = \frac{1-d}{d}\implies K=\frac{N(1-d)}{d}, \end{gathered} \] und der Preis der Anleihe wäre dann (Einsetzen in (2.16)): \[ \begin{gathered} P= \frac{N(1-d)}{d}\,d\,\frac{1-d^T}{1-d}+Nd^T=N, \end{gathered} \] Nominale und Preis der Anleihe stimmen überein, die Anleihe notiert dann pari. □

Die nächste Aufgabe bringt einen neuen, interessanten Aspekt ins Spiel.

Musteraufgabe 2.34 Zur Finanzierung einer vorschüssigen Rente der Höhe \(15\,000\) GE steht ein Kapital von \(200\,000\) GE zur Verfügung. Wie viele Jahre kann die Rente ausbezahlt werden, wenn der Zinssatz 4% beträgt?

Lösung: Wir haben bisher den Barwert eines Zahlungsstroms (Rente) als Gegenwartswert der in Zukunft zu erwartenden Zahlungen interpretiert. Dies war die Sicht der Begünstigten, der Empfänger der Zahlungen. Wie aber stellt sich die Lage dar aus Sicht derer, die zur Zahlung verpflichtet sind?

Für sie ist der Barwert der Rente das Kapital, das zur Finanzierung des Zahlungsstroms herangezogen wird. Dazu brauchen wir nur die Darstellung (2.11) aus der Position der die Rente Leistenden zu betrachten.

Vor dem Hintergrund dieser Überlegungen lesen wir die Angabe nun so: das Rentenkapital von 200 000 GE ist der Barwert \(B_t\) einer vorschüssigen Rente mit Zahlung \(a=15\,000\) und Verzinsung mit \(r=0.04\). Unsere Aufgabe besteht nun darin die Bezugszeit \(T\) zu berechnen. Dazu verwenden wir die vorschüssige Barwertformel (2.11), die wir nach \(T\) auflösen. Wir gehen so vor: zuerst formen wir (2.11) um: \[ \begin{gathered} B_T=a\frac{1-d^T}{1-d}\implies d^T=1-\dfrac{B}{a}\cdot (1-d) \end{gathered} \] Einsetzen ergibt die Exponentialgleichung: \[ \begin{gathered} \left(\frac{1}{1.04}\right)^T=1-\frac{200000}{15000} \left(1-\frac{1}{1.04}\right) = 0.487179\,. \end{gathered} \] Mit Hilfe von Logarithmen finden wir die Lösung \(T = 18.335278\).

Mit anderen Worten: das Rentenkapital ist ausreichend, um 18 Zahlungen in voller Höhe zu finanzieren. □

Zwei interessante Fragen stellen sich nun.

1.) Was ist das Rentenkapital am Beginn des 19. Jahres?

Wir beantworten diese Frage etwas allgemeiner: wenn ein Rentenkapital \(K\) zur vorschüssigen Finanzierung von \(T\) Zahlungen der Höhe \(a\) reicht, was ist das Restkapital \(R_T\) zu Beginn des Jahres \(T+1\)?

Der Bewertungszeitpunkt \(T\) liegt in der Zukunft, daher ergibt sich der Rest \(R_T\) aus dem Endwert des Rentenkapitals \(K\) abzüglich des Endwerts der vorschüssig geleisteten Zahlungen \(a\). Mit (2.13): \[ \begin{gathered} R_T=Kq^T-aq\frac{q^T-1}{q-1} \end{gathered} \] Mit den Daten der letzten Aufgabe, insbesondere \(q=1.04\): \[ \begin{gathered} R_{18}=200000\cdot q^{18}-15000\cdot q\cdot\frac{q^{18}-1}{q-1}= 5094.862078\simeq 5095\,. \end{gathered} \] Mit anderen Worten, das Restkapital am Beginn des 19. Jahres beträgt 5095 GE.

Interessanter ist die Frage:

2.) Wie reagiert die Bezugszeit \(T\) auf Änderungen der Zahlung \(a\)?

Intuitiv ist die Sache klar: wenn wir \(a\) erhöhen, dann ist das Kapital \(K\) schneller verbraucht und \(T\) nimmt ab. Umgekehrt, wenn wir \(a\) verringern, dann reicht das Kapital länger, also wird \(T\) größer.

Womit sich aber sofort eine weitere Frage ergibt:

3.) Wie groß kann \(T\) maximal werden?

Die Antwort auf die letzte Frage lautet: \(T\) kann beliebig, d.h. unendlich groß werden, wenn die Zahlung \(a\) nur ausreichend niedrig ist. Diese Überlegungen führen uns auf einen weiteren wichtigen Begriff.

2.4.2 Ewige Renten

Eine ewige Rente ist dadurch charakterisiert, dass die jährlichen Zahlungen \(a\) exakt gleich sind den jährlichen Zinserträgen des Rentenkapitals. Das bedeutet:

• Das Rentenkapital bleibt im Zeitablauf unverändert;

• Die Zahlungen können ohne zeitliches Limit finanziert werden.

Bezeichnen wir mit \(B_\infty\) das Basiskapital einer ewigen Rente, also ihren Barwert. Untersuchen wir den nachschüssigen Fall zuerst: am Jahresende wird ein Betrag ausbezahlt, der exakt dem Zinsertrag dieses Jahres entspricht, d.h. \(a=rB_\infty\). Damit ergibt sich für den Barwert der nachschüssigen ewigen Rente: \[ \begin{gathered} B_\infty = \frac{a}{r} = \frac{ad}{1-d}, \end{gathered} \tag{2.17}\] weil ja \(d=1/(1+r)\) und daher \(r=(1-d)/d\). Werden hingegen die Zahlungen vorschüssig geleistet, dann müssen die Einzelzahlungen \(a\) um ein Jahr weniger oft abgezinst werden, wir dividieren deshalb (2.17) durch \(d\): \[ \begin{gathered} B_\infty = \frac{a(1+r)}{r}=\frac{a}{1-d}. \end{gathered} \tag{2.18}\] Klassische Fälle von ewigen Renten sind Stiftungen, deren Zinsertrag dazu dient gewisse (häufig gemeinnützige) Vorhaben regelmäßig zu finanzieren. Das berühmteste Beispiel ist zweifellos die im Jahr 1900 eingerichtete Alfred Nobel Stiftung. Sie war ursprünglich ausgestattet mit einem Grundkapital von 31 Mio. Schwedische Kronen. Heute beträgt das Stiftungskapital ca. 3 Milliarden Kronen (350 Mio. Euro).

Abgesehen davon treffen wir regelmäßig dann auf ewige Renten, wenn wir es mit zeitlich nicht limitierten Dauerschuldverhältnissen zu tun haben, wie z.B. unbefristete Miet- und Pachtverträge und dergleichen.

Musteraufgabe 2.35 Welches Kapital ist nötig, um bei einem Zinssatz von 8 % eine vorschüssige ewige Rente in Höhe von 1000 GE finanzieren zu können?

Lösung: Mit (2.18) finden wir: \[ \begin{gathered} B_\infty = \frac{1000(1+0.08)}{0.08}= 13500. \end{gathered} \] □

Musteraufgabe 2.36 Der Betreiber eines Einkaufsmarkts hat seinen Kundenparkplatz auf einem gepachteten Grundstück angelegt. Der Pachtvertrag ist unbefristet, die jährliche, am Jahresende zu bezahlende Pacht für das Grundstück beträgt 200 000 GE.

Das Management des Marktes möchte das Grundstück käuflich erwerben, um so die dauerhafte finanzielle Belastung durch den Pachtzins aus der Welt zu schaffen. Bei einem langfristigen Marktzins von 4%:

• Was wäre ein fairer Kaufpreis?

• Was wäre die zu bezahlende (nachschüssige) Rate, wenn dieser Kaufpreis auf fünf Jahre gleichmäßig verteilt wird?

Lösung: Da der Pachtvertrag unbefristet ist, generieren die Pachtzahlungen des Unternehmens an die Eigentümer des Grundstücks einen Zahlungsstrom, der einer nachschüssigen ewigen Rente entspricht. Mit (2.17) errechnen wir den fairen Kaufpreis als Barwert dieser Rente: \[ \begin{gathered} B_\infty = \frac{200000}{0.04} = 5\,000\,000\,. \end{gathered} \] Die Ratenzahlungen, nennen wir sie \(R\), bilden eine nachschüssige Rente mit Barwert, der sich aus (2.12) ergibt. Dieser muss gleich sein dem Barwert der ewigen Rente (2.17) mit Zahlung \(a\). Ganz allgemein also: \[ \begin{gathered} \frac{ad}{1-d}=Rd\frac{1-d^t}{1-d}\implies R=\frac{a}{1-d^t}. \end{gathered} \] Mit unseren Angaben: \[ \begin{gathered} R=\frac{200000}{1-(1/1.04)^5} = 1123135.57\,. \end{gathered} \] Die Jahresraten betragen damit ca. 1 123 136 GE. □

2.4.3 Ewige Anleihen

Ewige Renten werden auch gelegentlich als Finanzierungsinstrumente eingesetzt, man spricht dann von ewigen Anleihen, engl. consols (von consolidated) oder perpetuities.

Die Idee: Der Schuldner erhält vom Gläubiger Kapital, das er nie zurückzahlen muss. Dafür verpflichtet sich der Schuldner zeitlich unbefristet (ad infinitum) Zinsen zu bezahlen.

Diese Konstruktion hat für Gläubiger Vorteile und Nachteile:

• Vorteile: Bei guten Schuldnern sehen sich Gläubiger einem langfristig stabilen Zahlungsstrom gegenüber.

• Nachteile: Gläubiger tragen ein Inflationsrisiko und ein Insolvenzrisiko. Letzteres, weil diese Schuld im Insolenzfall typischerweise nachrangiges Kapital ist. Diese Nachteile werden im allgemeinen kompensiert durch höhere Zinssätze.

Die älteste, noch aktive ewige Anleihe von 1000 Karolusgulden wurde 1648 in den Niederlanden begeben. Die Mittel dienten seinerzeit zur Finanzierung eines Hochwasserdeichs. Die Anleihe wird heute noch bedient, aktuell (2018) beträgt der Kupon der Anleihe 11.34 Euro.

Heute werden ewige Anleihen sowohl von Staaten als auch von großen Unternehmen aufgelegt. Ein aktuelles Beispiel ist die börsennotierte Raiffeisen Bank International (RBI). Mitte 2017 legte sie in Polen eine ewige Anleihe in der Höhe von 650 Mio. Euro auf, ausgestattet mit einem Zinskupon von 6.125 %. Diese Anleihe war innerhalb weniger Stunden dreifach überzeichnet.

Musteraufgabe 2.37 Eine Nullkupon-Anleihe mit Emissionsvolumen 100 Mio., Laufzeit 10 Jahre und Zinssatz 4% soll nach 5 Jahren in eine ewige Anleihe mit Zinssatz 6 % umgewandelt werden. Welcher Betrag muss jährlich (nachschüssig) an die Zeichner dieser Anleihe ausgeschüttet werden?

Lösung: Der Preis (Barwert) der ewigen Anleihe ist der 5-jährige Endwert des Emissionsvolumens bei 4 % Zinsen: \[ \begin{gathered} B_\infty = 100\,000\,000\cdot 1.04^5 = 121\,665\,290.24\,. \end{gathered} \] Die jährlichen Zahlungen ergeben sich bei einem Zinssatz von 6% aus (2.17): \[ \begin{gathered} a=r B_\infty=0.06\cdot 121\,665\,290.24 = 7\,299\,917.4144\text{ GE}. \end{gathered} \] Zu bedenken ist dabei, dass diese Zahlungen ad infinitum zu leisten sind, während die aushaftende Schuld \(B_\infty\) von ca. 121 Mio. unverändert bleibt. □

2.5 Unterjährige Verzinsung

Es ist im Bankwesen üblich, nicht nur am Jahresende Zinsen gutzuschreiben (dh. für die Bildung von Zinseszinsen freizugeben), sondern auch zu bestimmten Stichtagen während des Jahres. Teilt man das Jahr in zwei Verzinsungsperioden ein, dann wird halbjährlich verzinst, bei vier Verzinsungsperioden spricht man von vierteljährlicher Verzinsung. Die Grundlage der Verzinsung bildet der nominelle Jahreszinssatz \(c\). Dabei handelt es sich keineswegs um die Kapitalrendite eines ganzen Jahres, sondern nur um eine rechnerische Größe, von der aus der Zinssatz für die unterjährige Verzinsung gebildet wird.

Es sei \(c\) der nominelle Jahreszinssatz. Wenn das Jahr in \(k\) gleich lange Verzinsungsperioden eingeteilt wird, dann wird am Ende jeder Periode das Kapital mit dem Zinssatz \(c/k\) verzinst. Der nominelle Jahreszinssatz wird also gleichmäßig auf die \(k\) Verzinsungsperioden eines Jahres aufgeteilt. Ein Anfangskapital \(K_0\) wächst so im Laufe eines Jahres zum Endkapital \(K_1\) an: \[ \begin{gathered} K_1=\Big(1+\dfrac{c}{k}\Big)^k\cdot K_0. \end{gathered} \] Man kann nun die naheliegende Frage stellen, welcher Jahreszinssatz das gleiche Ergebnis erzielen würde. Das ist ein Äquivalenzproblem. Ein äquivalenter Jahreszinssatz \(r\) muss nach einem Jahr dasselbe Kapital \(K_1\) ergeben und somit die Gleichung \[ \begin{gathered} 1+r=\Big(1+\frac{c}{k}\Big)^k \end{gathered} \tag{2.19}\] erfüllen. Daraus folgt \[ \begin{gathered} r=\Big(1+\frac{c}{k}\Big)^k-1. \end{gathered} \] Man nennt \(r\) den effektiven Jahreszinssatz.

Praktisch ändert sich für uns durch Einführung der Unterjährigkeit nur wenig, wir müssen nur den Aufzinsungsfaktor entsprechend anpassen:

Vergleich jährliche und unterjährige Verzinsung

Es gilt nach wie vor die Endwertgleichung: \[ \begin{gathered} K_t=K_0q^t \end{gathered} \]

• Jährliche Verzinsung mit effektivem Zinssatz \(r\):
  \(\implies q=1+r\)

• \(k\)-mal pro Jahr verzinst mit nominellem Zinssatz \(c\):
  \(\displaystyle\implies q =\left(1+\frac{c}{k}\right)^k\)

Musteraufgabe 2.38 Ein Anfangskapital von \(10000\) GE wird mit nominellem Jahreszins von 4 % monatlich verzinst. Was ist sein Endwert nach 10 Jahren?

Lösung: Der Aufzinsungsfaktor für ein Jahr beträgt: \[ \begin{gathered} q=\left(1+\frac{0.04}{12}\right)^{12}. \end{gathered} \] Mit der klassischen Endwertformel ergibt sich: \[ \begin{gathered} K_{10}=K_0q^ {10}=10000\left(1+\frac{0.04}{12}\right)^{12\cdot 10}=14908.3268 \text{ GE}. \end{gathered} \] Zum Vergleich: würde mit 4 % einmal pro Jahr verzinst, dann beträgt der Endwert nur: \[ \begin{gathered} K_{10}=10000(1+0.04)^{10}=14802.4428\,. \end{gathered} \] □

Musteraufgabe 2.39 Eine Bausparkasse verzinst Darlehen mit dem nominellen Jahreszinssatz von 6 % bei vierteljährlicher Verzinsung. Wie hoch ist der effektive Jahreszinssatz?

Lösung: Wir verwenden (2.19) und errechnen daraus den effektiven Jahreszinssatz: \[ \begin{gathered} r=\Big(1+\frac{c}{k}\Big)^k-1=\Big(1+\frac{0.06}{4}\Big)^4-1=0.06136 \text{ Prozent}. \end{gathered} \] Dies entspricht einem effektiven Zinssatz von ca. 6.14 %. Wir beobachten, dass der effektive Jahreszinssatz höher ist als der nominelle Jahreszinssatz. □

Eine interessante Frage ist, wie man bei gegebenem effektiven Jahreszinssatz und gegebener unterjähriger Periodenzahl den nominellen Zinssatz ausrechnet. Wir sehen uns zunächst ein Beispiel an.

Musteraufgabe 2.40 Ein Kapital wird vierteljährlich mit dem effektiven Zinssatz von 8.5% verzinst. Wie hoch ist der nominelle Zinssatz?

Lösung: In die Grundgleichung (2.19), \[ \begin{gathered} 1+r = \left(1+\dfrac{c}{k}\right)^k, \end{gathered} \] setzen wir die gegebenen Zahlen ein: \[ \begin{gathered} 1+0.085 =\left(1+\dfrac{c}{4}\right)^4, \end{gathered} \] und errechnen durch eine einfache Umformung den nominellen Zinssatz \(c\): \[ \begin{gathered} c=(\sqrt[4]{1.085}\;-\;1)\cdot 4 = 0.0824\,. \end{gathered} \] Der nominelle Zinssatz beträgt also 8.24%. □

Allgemein ergibt sich, dass \[ \begin{aligned} \left(1+\frac{c}{k}\right)^k = 1+r &\implies 1+\frac{c}{k}=(1+r)^{1/k}\\ &\implies c=k\left((1+r)^{1/k}-1\right). \end{aligned} \tag{2.20}\]

Musteraufgabe 2.41 Eine Kreditbüro möchte Darlehen mit einem effektiven Jahreszinssatz von 11 Prozent zu Verfügung stellen. Es soll allerdings nur der nominelle Zinssatz bei monatlicher Verzinsung veröffentlicht werden. Wie hoch muss der nominelle Zinssatz gewählt werden?

Lösung: Nun ist \(k=12\) und wir berechnen den nominellen Zinssatz mit Hilfe von (2.20): \[ \begin{gathered} c=k\Big((1+r)^{1/k}-1\Big)=12( 1.11^{1/12}-1)=0.1048\,. \end{gathered} \] Mit anderen Worten, der nominelle Zinssatz beträgt 10.48 %. □

Musteraufgabe 2.42 Ein Kapital von 10 000 GE steigt in 5 Jahren auf 15 228 GE bei vierteljährlicher Verzinsung. Wie hoch ist der nominelle Zinssatz?

Lösung: Es gilt, siehe die Übersicht (2.19) , nach wie vor die Endwertgleichung mit entsprechend angepasstem Aufzinsungsfaktor: \[ \begin{gathered} K_5=15228 = 10000\cdot q^5=10000\left[\left(1+\frac{c}{4}\right)^4\right]^5\\[5pt] 15228 = 10000\left(1+\frac{c}{4}\right)^{20}. \end{gathered} \] Daraus finden wir: \[ \begin{gathered} 1+\dfrac{c}{4}=\left(\dfrac{15228}{10000}\right)^{1/20} \quad\Rightarrow\quad c=0.085\,. \end{gathered} \] Es wird daher mit 8.5 % nominell verzinst. □

2.6 Exponentialfunktion und Logarithmus

2.6.1 Exponentialfunktionen

Wir können durch die Bildung von Potenzen \(a^p\) Funktionsterme definieren. Dabei haben wir zwei Möglichkeiten für die Wahl der Funktionsvariablen. Wenn wir die Basis der Potenz als Funktionsvariable heranziehen, also \(f(x)=x^p\) bilden, dann entsteht eine Potenzfunktion.

Nun definieren wir Funktionen mit Potenztermen, indem wir den Exponenten als Variable verwenden; wir bilden also \(f(x)=a^x\). Solche Funktionen nennt man Exponentialfunktionen.

Definition 2.43 Es sei \(a>0\). Eine Funktion mit dem Funktionsterm \(f(x)=a^x\) heißt
Exponentialfunktion.

Exponentialfunktionen sind eng verwandt mit geometrischen Folgen. Wenn wir für die Variable \(x\) nur die natürlichen Zahlen \(t=1,2,3\ldots\) einsetzen, dann entsteht \[ \begin{gathered} f(1)=a,\;f(2)=a^2,\;f(3)=a^3,\ldots,\,f(n)=a^n, \end{gathered} \] das ist eine geometrische Folge mit dem Quotienten \(a\).

Die Abbildung 2.6 zeigt typische Graphen von Exponentialfunktionen. Wir können daraus die qualitativen Eigenschaften von Exponentialfunktionen ablesen, die in der folgenden Übersicht aufgelistet sind.

Abbildung 2.6: Graph von \(a^x\) für \(a>1\) und \(0<a<1\).

Eigenschaften von Exponentialfunktionen

• Eine Exponentialfunktion ist für alle reellen Zahlen definiert.

• Eine Exponentialfunktion nimmt nur positive Zahlen als Werte an.

• Eine Exponentialfunktion ist stetig.

• Der Graph einer Exponentialfunktion geht durch den Punkt \((0,1)\).

• Der Graph der Exponentialfunktion geht durch den Punkt \((1,a)\).

• Ist \(a>1\), dann ist die Exponentialfunktion streng monoton wachsend.

• Ist \(0<a<1\), dann ist die Exponentialfunktion streng monoton fallend.

• Eine Exponentialfunktion ist auf endlichen Intervallen beschränkt, aber auf \(\mathbb R\) unbeschränkt.

• Eine Exponentialfunktion ist konvex, ihr Graph ist glatt.

Worin besteht nun die praktische Bedeutung von Exponentialfunktionen? Um dies zu beantworten, untersuchen wir die relative (prozentuelle) Änderung einer Exponentialfunktion. Allgemein versteht man unter der relativen Änderung einer Funktion \(f\) auf einem beliebigen Intervall \([x,x+1]\) der Länge 1 die Größe \[ \begin{gathered} \frac{f(x+1)-f(x)}{f(x)}. \end{gathered} \] Wir betrachten nun eine Funktion mit dem Term \(f(x)=Aa^x\). Abgesehen vom Faktor \(A\) ist das eine Exponentialfunktion. Funktionen der Form \(f(x)=Aa^x\) haben die bemerkenswerte Eigenschaft, dass die relative Änderung auf einem Intervall der Länge 1 konstant ist.

Für Exponentialfunktionen gilt nämlich: \[ \begin{gathered} \frac{f(x+1)-f(x)}{f(x)}= \frac{Aa^{x+1}-Aa^{x}}{Aa^x}=a-1 \quad \text{für alle $x \in \mathbb R$}. \end{gathered} \tag{2.21}\] Bezeichnet man diese Größe mit \(r:=a-1\), dh. \(a=1+r\), dann lässt sich diese charakteristische Eigenschaft der Exponentialfunktionen so ausdrücken:

Satz 2.44 Eine Exponentialfunktion \(f(x)=Aa^x=A(1+r)^x\) ändert sich auf Strecken der Länge \(1\) immer um denselben Prozentsatz \(r\). Insbesondere ist also die relative Änderung auf solchen Intervallen immer gleich groß.

Die Zahl \(a\) bezeichnet man als den Wachstumsfaktor. Ist der Wachstumsfaktor \(a>1\), so ist die relative Änderung \(r>0\) und der Funktionsgraph der Exponentialfunktion steigt monoton an. Ist der Wachstumsfaktor dagegen \(a<1\), so ist die relative Änderung \(r<0\) (relative Abnahme) und der Funktionsgraph der Exponentialfunktion fällt monoton ab.

Wir haben eine ähnliche Eigenschaft schon bei geometrischen Folgen beobachtet. Exponentialfunktionen sind das kontinuierliche Gegenstück zu geometrischen Folgen. Sie sind im Gegensatz zu Folgen nicht an diskrete Punkte \(n=1,2,\ldots\) gebunden, sondern sind in der Lage, einen kontinuierlichen Zustandsverlauf mit konstantem relativen Wachstum zu beschreiben.

Der Umstand, dass die relative Änderung von Exponentialfunktionen konstant ist, macht die praktische Bedeutung dieser Funktionenklasse aus.

Beispiel 2.45 (Kontinuierliches Populationswachstum)

Das jährliche Wachstum einer biologischen Population ist (bei idealen Lebensbedingungen) in der Regel proportional zur Größe der Population. Das bedeutet nichts anderes, als dass der relative Zuwachs pro Zeiteinheit konstant ist. Daher ist eine Exponentialfunktion geeignet, das Wachstum der Population zu beschreiben.

Es sei \(A\) der Anfangsbestand der Population zum Zeitpunkt \(t=0\). Die Population verändere sich in Zeitintervallen der Länge 1 um den Prozentsatz \(r\). Setzen wir \(a=1+r\), dann beträgt die Größe der Population zum Zeitpunkt \(1\) genau \(f(1)=A(1+r)=Aa^1\). Zu anderen Zeitpunkten \(t>0\) ergibt sich die Größe der Population durch \(f(t)=A(1+r)^t=Aa^t\).

Musteraufgabe 2.46 Eine Population mit dem Anfangsbestand \(f(0)=5000\) wächst in 10 Jahren insgesamt um 12 %. Wie groß ist die Population nach 2.5 Jahren? Wie lange dauert es, bis sich ihre Größe verdoppelt hat?

Lösung: Es muss die Funktion \(f\) aufgestellt werden, die die Populationsgröße als Funktion der Zeit \(t\) angibt. Wir nehmen an, dass die Population kontinuierlich mit konstantem relativen Zuwachs wächst und die Populationsgröße daher durch eine Exponentialfunktion \(f(t)=Aa^t\) beschrieben werden kann.

Aus \(f(0)=Aa^0=5000\) folgt \(A=5000\). Weil die Population innerhalb von 10 Jahren um 12 % wächst, ergibt sich die Basis \(a\) der gesuchten Exponentialfunktion aus der Gleichung \[ \begin{gathered} f(10)=1.12f(0). \end{gathered} \] Daraus folgt \[ \begin{gathered} \frac{f(10)}{f(0)}=a^{10}=1.12 \implies a=1.12^{1/10}=1.0114. \end{gathered} \] Also lautet die Wachstumsfunktion \(f(t)=5000\cdot1.0114^t.\) Nach 2.5 Jahren hat die Population die Größe \[ \begin{gathered} f(2.5)=5000\cdot 1.0114^{2.5}=5143.720687\simeq 5144 \end{gathered} \] erreicht. Für die Verdopplungszeit lösen wir die Gleichung: \[ \begin{gathered} f(t)=10000=5000\cdot 1.0114^t\implies 1.0114^t=2\,. \end{gathered} \] Diese Exponentialgleichung besitzt die Lösung: \[ \begin{gathered} t=\frac{\log(2)}{\log(1.0114)}=61.148303\simeq 61\text{ Jahre}. \end{gathered} \] □

2.6.2 Kontinuierliche Verzinsung

Wir untersuchen, wie sich bei unterjähriger Verzinsung eine immer stärkere Verkürzung der Verzinsungsperioden auf den effektiven Jahreszins auswirkt.

Die Eulersche Zahl

Zunächst betrachten wir der Einfachheit halber einen etwas unrealistischen Fall, bei dem wir annehmen, der nominelle Jahreszinssatz betrage \(c=100\,\%=1\). Bei \(n\) Verzinsungsperioden beträgt daher der Aufzinsungsfaktor für ein Jahr: \[ \begin{gathered} q_n=\left( 1+\frac{1}{n} \right)^n. \end{gathered} \tag{2.22}\] Wir berechnen nun diese Aufzinsungsfaktoren für 1, 4, 12, usw. Zinstermine pro Jahr. Die folgende Tabelle enthält einige Glieder der so entstehenden Folge.

\[ \begin{array}{lll} \hline \text{Verzinsung} & n & (1+1/n)^n \\ \hline \text{jährlich} & 1 & 2 \\ \text{vierteljährlich} & 4 & 2.44 \\ \text{monatlich} & 12 & 2.613 \\ \text{wöchentlich} & 52 & 2.693 \\ \text{täglich} & 365 & 2.71457 \\ \text{stündlich} & 8760 & 2.7181267 \\ \hline \end{array} \]

Die Abbildung 2.7 zeigt den Graphen der Folge. Wir haben den Eindruck, dass die Folge \(q_n\) monoton wächst und beschränkt ist. Beide Eigenschaften lassen sich auch mathematisch exakt beweisen, was wir aber hier nicht tun wollen.

Abbildung 2.7: Die ersten 12 Glieder der Folge \(q_n=(1+1/n)^n\).

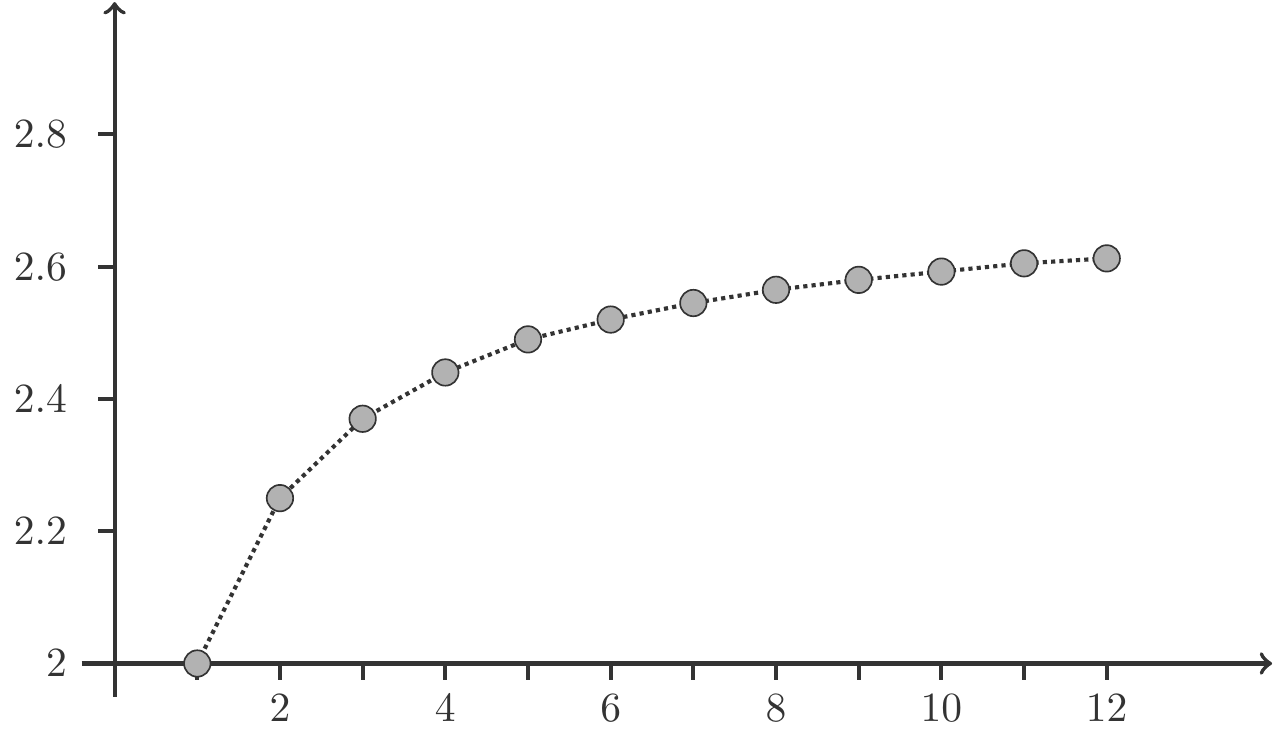
Wir interessieren uns für die Frage, ob die Folge einen Limes besitzt. Wenn ein solcher Limes existiert, hat er eine interessante praktische Bedeutung. Ein solcher Limes entspricht dann der Vorstellung eines Aufzinsungsfaktors, der entsteht, wenn man mit unendlich vielen unendlich kleinen Verzinsungsperioden Zinseszinsen berechnet. Man spricht dann von kontinuierlicher Verzinsung.

Allerdings ist es nicht möglich, auf einfache Weise einen Limes festzustellen, indem man ihn durch irgendwelche Umformungen des Folgenterms als Formel darstellt. Es ist vielmehr so, dass die Folge \(q_n\) auf Grund allgemeiner mathematischer Prinzipien, einen Limes besitzen muss⁴. Eine einfache Formel für den Limes kann man jedoch nicht angeben. Der Limes ist eine irrationale Zahl, die man numerisch nur näherungsweise angeben kann. Er wird mit dem Buchstaben \(e\) bezeichnet und hat den Wert \[ \begin{gathered} e=2.7182818\ldots \end{gathered} \tag{2.23}\] Man nennt die Zahl \(e\) die Eulersche Zahl. Es gilt also \[ \begin{gathered} \lim_{n\to\infty} \left( 1+\frac{1}{n} \right)^n=e, \end{gathered} \tag{2.24}\] und diese Zahl \(e\) ist der Aufzinsungsfaktor bei kontinuierlicher Verzinsung mit dem nominellen Zinssatz \(c=1\).

Definition 2.47 Die Zahl \[ \begin{gathered} e:=\lim_{n\to\infty} \Big(1+\frac{1}{n}\Big)^n \end{gathered} \] heißt die Eulersche Zahl.

Aufzinsungsfaktoren

Die praktische Bedeutung der Eulerschen Zahl \(e\) im finanzmathematischen Kontext wird durch die folgenden Überlegungen deutlich.

Ein Kapital werde mit dem nominellen Zinssatz \(c>0\) unterjährig mit \(n\) Perioden verzinst. Der Aufzinsungsfaktor beträgt \[ \begin{gathered} q_n=\left(1+\frac{c}{n}\right)^n. \end{gathered} \] Wenn wir kontinuierliche Verzinsung mit dem nominellen Zinssatz \(c\) vornehmen wollen, müssen wir die Anzahl \(n\) der Perioden gegen Unendlich wachsen lassen. Was passiert dabei mit der Folge \(q_n\) der Aufzinsungsfaktoren?

Auch diese Folge ist monoton wachsend und beschränkt. Wenn wir den Graphen zeichnen, können wir dies nachvollziehen. Aus diesen beiden Eigenschaften kann man (mit mathematischen Argumenten) schließen, dass auch diese Folge für jede Wahl von \(c\) konvergent sein und einen Limes besitzen muss. Doch wie findet man diesen Limes?

Es ist bemerkenswert, dass der gesuchte Limes in einem sehr engen Zusammenhang zur Eulerschen Zahl \(e\) steht. Es gilt nämlich \[ \begin{gathered} \lim_{n\to\infty} \left(1+\frac{c}{n}\right)^n=e^c. \end{gathered} \tag{2.25}\] Diese Formel ist so wichtig, dass wir ihre Aussage nochmals in Worten formulieren:

Satz 2.48 Wird ein Kapital mit dem nominellen Zinssatz \(c\) eine Periode lang kontinuierlich verzinst, dann beträgt der Aufzinsungsfaktor \(q=e^c\).

Da eine exakte Begründung dieser Tatsache unsere Möglichkeiten übersteigt, überzeugen wir uns durch numerische Experimente (z.B. mit dem Taschenrechner) von der Gültigkeit der Formel.

Es sei \(c=0.08\). Das heißt, wir verzinsen mit dem nominellen Zinssatz von 8 Prozent. Die folgende Tabelle enthält einige Werte der Folge \(q_n\).

\[ \begin{array}{lll} \hline \text{Verzinsung} & n & (1+c/n)^n \\ \hline \text{jährlich} & 1 & 1.08 \\ \text{vierteljährlich} & 4 & 1.08234 \\ \text{monatlich} & 12 & 1.08300 \\ \text{wöchentlich} & 52 & 1.08322 \\ \text{täglich} & 365 & 1.08328 \\ \text{stündlich} & 8760 & 1.08329 \\ \hline \end{array} \]

Wir vergleichen nun die Aufzinsungsfaktoren in der Tabelle mit dem Limes aus (2.25). Es ist \(e^{0.08}=1.083287\ldots\) Dies zeigt eine ausgezeichnete Übereinstimmung mit der Voraussage der Formel (2.25).

Kapitalverzinsung

Es sei \(K(t)\) die Höhe eines Kapitals, das mit dem nominellen Zinssatz \(c\) kontinuierlich verzinst wird. Wir wissen, dass dann der Aufzinsungsfaktor für eine Periode \(q=e^c\) beträgt und dass daher das Kapital nach einer Periode die Höhe \(K(1)=K(0)q=K(0)e^c\) erreicht.

Bei kontinuierlicher Verzinsung werden Zinseszinsen aber nicht nur nach jeweils vollendeten Perioden gutgeschrieben, sondern auch nach jedem Bruchteil einer Periode. Ist zum Beispiel \(t\) irgendein beliebiger Zeitpunkt, dann wächst das Kapital im Zeitintervall \([t,t+1]\) ebenfalls um den Faktor \(q=e^c\), dh. \[ \begin{gathered} K(t+1)=K(t)q=K(t)e^c. \end{gathered} \] Daher ist der relative Zuwachs \[ \begin{gathered} \frac{K(t+1)-K(t)}{K(t)}=\frac{K(t)e^c-K(t)}{K(t)}=e^c-1=:r \end{gathered} \] konstant und \(K(t)\) ist eine Exponentialfunktion, darstellbar in der Form \[ \begin{gathered} K(t)=Aa^t \quad\text{mit}\quad a=1+r=e^c=q. \end{gathered} \] Daraus ergibt sich, dass \(A=K(0)\) sein muss und wir erhalten schließlich \[ \begin{gathered} K(t)=K(0)(1+r)^t=K(0)q^t=K(0)e^{ct}. \end{gathered} \tag{2.26}\] Kontinuierliche Kapitalverzinsung wird also durch eine Exponentialfunktion mit der Basis \(a=1+r=q=e^c\) beschrieben.

Erneut erkennen wir, dass wie beim Übergang von jährlicher zu unterjähriger Verzinsung sich nichts Wesentliches ändert. Nach wie vor gilt die vertraute Endwertformel, allein der Aufzinsungsfaktor ist entsprechend anzupassen. Daher ergänzen wir unser Übersicht (2.19):

Vergleich jährliche, unterjährige und kontinuierliche Verzinsung

Es gilt die Endwertgleichung: \[ \begin{gathered} K_t=K_0q^t \end{gathered} \]

• Jährliche Verzinsung mit effektivem Zinssatz \(r\):
  \(\implies q=1+r\)

• \(k\)-mal pro Jahr verzinst mit nominellem Zinssatz \(c\):
  \(\displaystyle\implies q =\left(1+\frac{c}{k}\right)^k\)

• Kontinuierliche Verzinsung mit nominellem Zinssatz \(c\);
  \(\implies q=e^c\)

Musteraufgabe 2.49 Ein Kapital von 2 500 GE wird mit dem nominellen Zinssatz von 7.5 % kontinuierlich verzinst. Wie hoch ist das Kapital nach 6 Jahren?

Lösung: Der Aufzinsungsfaktor für ein Jahr beträgt \(q=e^{0.075}\). Wir erhalten daher das Kapital nach 6 Jahren durch \[ \begin{gathered} K_6=K_0q^6=2\,500\,(e^{0.075})^6=2\,500\,e^{0.45}=3\,920.78. \end{gathered} \] □

Musteraufgabe 2.50 Ein Kapital wird mit \(7\%\) nominell verzinst. Wie hoch ist der effektive Zinssatz bei kontinuierlicher Verzinsung?

Lösung: Wir bezeichnen wieder den nominellen Zinssatz mit \(c\) und den effektiven Zinssatz mit \(r\). Diese Größen hängen bei kontinuierlicher Verzinsung durch die Gleichung \(e^{c} = q = 1+r\) zusammen. Dies führt auf die Lösung folgender Gleichung: \[ \begin{aligned} e^{0.07}& = 1+r \\ r& = e^{0.07} - 1 \\ r& = 0.0725\,. \end{aligned} \] Das heißt, das Kapital wird mit jährlich mit 7.25 % effektiv verzinst. □

Musteraufgabe 2.51 Wie lange muss ein Kapital \(K\) mit einem nominellen Zinssatz von \(c=5\,\%\) kontinuierlich verzinst werden, damit es sich verdoppelt?

Lösung: Der Aufzinsungsfaktor für ein Jahr beträgt \(q=e^{0.05}\). Die erforderliche Periodenzahl \(n\) muss die Ungleichung \(q^t\ge 2\) erfüllen, weil wir ja verdoppeln wollen. Wir lösen daher die Gleichung \(K_0q^t=2K_0\), dh. \[ \begin{gathered} q^t=(e^{0.05})^t=e^{0.05\cdot t}=2. \end{gathered} \] Diese Exponentialgleichung hat die Lösung \[ \begin{gathered} t=\frac{\log 2}{0.05 \log e}=13.862944\simeq 14. \end{gathered} \] Das Kapital muss also mindestens 14 Perioden lang verzinst werden. □

2.6.3 Logarithmusfunktionen

Den Logarithmus kennen wir schon aus dem Abschnitt 2.2.1. Auch der Zusammenhang zwischen Potenzen und Logarithmen ist uns geläufig. Wir werden diese Zusammenhänge jetzt vertiefen.

Erinnern wir uns an die Definition des Logarithmus aus dem Abschnitt 2.2.1. Zu jeder positiven Zahl \(y>0\) gibt es einen Logarithmus \(x=\log y\), der durch die Eigenschaften \[ \begin{gathered} \log(10^x)=x \quad\text{und}\quad 10^{\log y}=y \end{gathered} \tag{2.27}\] gekennzeichnet ist. Der Logarithmus macht also die Aktion der Exponentialfunktion \(y=10^x\) rückgängig und umgekehrt. Wir sagen daher, die durch \(x=\log y\) definierte Funktion ist die inverse Funktion zur Exponentialfunktion \(y=10^x\).

Definition 2.52 Die Funktion \(\log: (0,\infty)\to \mathbb R\), die durch \(y=\log x\) definiert ist, heißt Logarithmusfunktion zur Basis 10.

Die Erwähnung der Basis 10 in der Definition der Logarithmusfunktion legt nahe, dass es auch noch andere Logarithmusfunktionen gibt. Wenn wir von einer Logarithmusfunktion schlechthin sprechen, meinen wir aber in Hinkunft immer die Logarithmusfunktion zur Basis 10. Hier die wichtigsten Eigenschaften der Logarithmusfunktion:

Eigenschaften der Logarithmusfunktion

• Die Logarithmusfunktion ist nur für positive Zahlen definiert.

• Die Logarithmusfunktion nimmt alle reellen Zahlen als Werte an.

• Die Logarithmusfunktion ist stetig.

• Der Graph der Logarithmusfunktion geht durch den Punkt \((1,0)\).

• Der Graph der Logarithmusfunktion geht durch den Punkt \((10,1)\).

• Die Logarithmusfunktion ist streng monoton wachsend.

• Eine Logarithmusfunktion ist in der Nähe von 0 und in der Nähe von \(\infty\) nicht beschränkt.

• Die Logarithmusfunktion ist konkav.

• Der Graph der Logarithmusfunktion ist glatt.

Jede Exponentialfunktion \(f(x)=a^x\) ist invertierbar, weil sie stetig und streng monoton ist. Für die spezielle Exponentialfunktion \(f(x)=10^x\) kennen wir die inverse Funktion schon. Es handelt sich einfach um die Logarithmusfunktion \(x=\log y\). Wie sehen aber die inversen Funktionen von Exponentialfunktionen mit einer anderen Basis aus?

Beispiel 2.53 (Inverse von Exponentialfunktionen)

Um die Exponentialfunktion \(f(x)=a^x\) zu invertieren, müssen wir die Gleichung \(y=a^x\) nach \(x\) auflösen. Das ist eine Exponentialgleichung. Wir logarithmieren beide Seiten der Gleichung \[ \begin{gathered} \log y= x \log a, \end{gathered} \] und erhalten als Lösung \[ \begin{gathered} x=\frac{\log y}{\log a}. \end{gathered} \] Die Funktion \[ \begin{gathered} g(y)=\frac{\log y}{\log a} \end{gathered} \] ist also die inverse Funktion der Exponentialfunktion \(f(x)=a^x\). Sie unterscheidet sich von der Logarithmusfunktion \(x=\log y\) nur durch die Multiplikation mit dem Faktor \(1/\log a\).

Es ist üblich, die inverse Funktion einer beliebigen Exponentialfunktion \(f(x)=a^x\) ebenfalls als Logarithmusfunktion zu bezeichnen, und zwar als Logarithmusfunktion zur Basis \(a\). Man verwendet die Bezeichnung \[ \begin{gathered} \log_a x:=\frac{\log x}{\log a}. \end{gathered} \tag{2.28}\] In diesem Sinn wäre unsere Logarithmusfunktion \(\log x=\log_{10} x\). Wir benötigen aber Logarithmusfunktionen mit verschiedenen Basen nicht, denn wir können beliebige Exponentialgleichungen lösen, indem wir eine einzige Logarithmusfunktion verwenden. Aus historischen Gründen hat sich dafür zunächst die Logarithmusfunktion zur Basis 10 durchgesetzt.

2.6.4 Exponentialfunktion und natürlicher Logarithmus

Leider ist es doch nicht so einfach, wie es sein könnte. Die Mathematik und die Wissenschaften, die Mathematik anwenden, haben sich zwar entschlossen, eine Vereinheitlichung von Exponentialfunktionen und Logarithmusfunktionen zu vollziehen. Aber es ist nicht die Basis 10, die sich endgültig als Basis für wissenschaftliche Anwendungen durchgesetzt hat.

Die Basis 10, die historisch zur Einführung von Logarithmen geführt hat, ist sehr zweckmäßig, wenn man Logarithmen dazu verwendet, numerische Berechnungen durchzuführen. Für mehrere Jahrhunderte war dies auch die hauptsächliche Anwendung von Logarithmen. Als es noch keine Taschenrechner und Computer gab, wurden Multiplikationen und Divisionen von Zahlen mit vielen Dezimalstellen mit Hilfe sogenannter Logarithmenbücher ausgeführt, was eine beträchtliche Zeitersparnis bedeutete. Heute ist diese Anwendung von Logarithmen völlig obsolet, und wenn dies die einzige Anwendung von Logarithmusfunktionen wäre, könnte man Logarithmen einfach vergessen.

Allerdings gibt es noch einen anderen sehr aktuellen (und zeitlosen) Anwendungsbereich von Exponentialfunktionen und ihren inversen Funktionen, den Logarithmusfunktionen. Es ist dies die mathematische Darstellung (Modellierung) von kontinuierlichen Wachstumsvorgängen. Wir haben zu Beginn dieses Kapitels schon Beispiele dieser Art kennengelernt.

Wenn man eine einheitliche Basis für Exponentialfunktionen und Logarithmusfunktionen festlegen will, die besonders zweckmäßig ist, um Wachstumsvorgänge zu beschreiben, dann ist die Basis 10 keineswegs zwingend. Im Gegenteil: Die Tatsache, dass Menschen zehn Finger⁵ haben, hat mit kontinuierlicher Verzinsung oder mit dem Wachstum von biologischen Populationen nicht das geringste zu tun.

Was wäre denn nun eine vernünftige Basis für Exponentialfunktionen, die natürliche kontinuierliche Wachstumsvorgänge beschreiben sollen? Eine Zahl bietet sich an, die wir schon in Zusammenhang mit der kontinuierlichen Verzinsung kennengelernt haben, nämlich die Eulersche Zahl \[ \begin{gathered} e=\lim_{n\to\infty} \Big(1+\frac{1}{n}\Big)^n=2.71828\ldots \end{gathered} \] Diese Zahl hat sich tatsächlich als einheitliche Basis für Exponentialfunktionen durchgesetzt. Es gibt triftige Gründe, die für die Wahl gerade der Eulerschen Zahl als Basis sprechen. Wir sind im Moment noch nicht in der Lage, diese Gründe wirklich nachzuvollziehen. Das werden wir aber im Kapitel 3 nachholen. Vorerst wollen wir die Tatsache einfach zur Kenntnis nehmen.

Definition 2.54 Die Funktion \(\exp\) ist definiert als die Exponentialfunktion \(\exp(x):=e^x\), \(x\in\mathbb R\), mit der Basis \(e\), wobei \(e\) die Eulersche Zahl bezeichnet. Diese spezielle Exponentialfunktion nennt man die Exponentialfunktion schlechthin.

Es ist kein sehr zweckmäßiger Sprachgebrauch, eine spezielle Exponentialfunktion als Exponentialfunktion ohne weiteres Attribut zu benennen und darauf zu hoffen, es würde stets aus dem Zusammenhang klar sein, was gemeint ist. Besser wäre es, die Funktion \(\exp\) als die natürliche oder die Eulersche Exponentialfunktion zu bezeichnen. Aber das ist nicht üblich. Hingegen zeichnet man die inverse Funktion von \(\exp\) durchaus mit einem Beinamen aus.

Definition 2.55 Die inverse Funktion von \(\exp\) heißt natürlicher Logarithmus und wird mit \(\ln\) bezeichnet.

Über die Gestalt der Graphen von \(\exp\) und \(\ln\) braucht man nicht viel Worte zu verlieren. Die Abbildung 2.8 zeigt genau das, was wir erwarten: Der Graph von \(y=\ln x\) entsteht offenbar durch Spiegelung des Graphen von \(y=\exp(x)\) an der Geraden \(y=x\).

Abbildung 2.8: Graph von \(f(x)=e^x\) und \(f(x)=\ln x\).

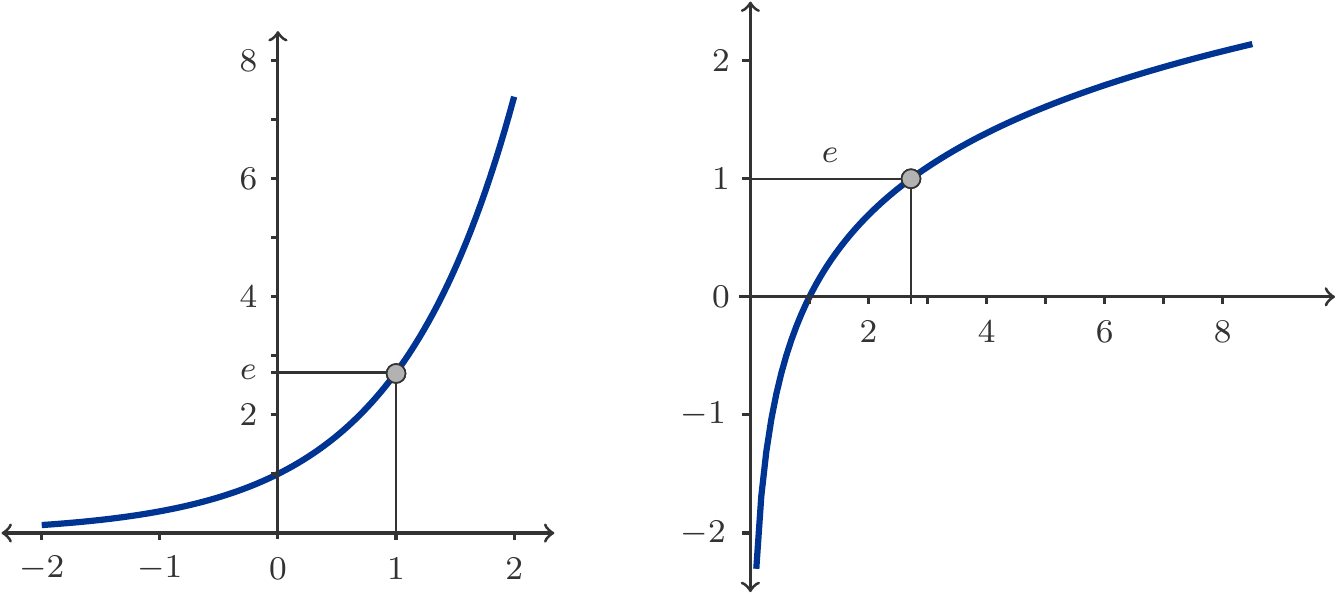
Rechengesetze

Beispiel 2.56 (Exponentialfunktion, natürlicher Logarithmus)

Jeder gute Taschenrechner ermöglicht die Berechnung von \(\exp(x)=e^x\). Wir gewöhnen uns an die Funktion durch die Berechnung von Beispielen: \[ \begin{gathered} \exp(2)=e^2=7.389056,\qquad \exp(-3.2)=e^{-3.2}=0.040762\,.\\[5pt] \exp(0.0512)=e^{0.0512}=1.052533\,. \end{gathered} \] Klar ist, dass \(\exp(1)=e^1=e\). Auch der natürliche Logarithmus sollte auf einem guten Taschenrechner direkt verfügbar sein: \[ \begin{gathered} \ln 3=1.098612, \quad \ln 1.5=0.405465, \quad \ln 0.53=-0.634878\,. \end{gathered} \] Wenn das aber nicht der Fall ist, können wir uns auch behelfen, indem wir uns erinnern, dass \[ \begin{gathered} y=e^x\quad\Rightarrow\quad \log y=\log e^x=x\log e \quad\Rightarrow\quad x=\frac{\log y}{\log e} \end{gathered} \] und daher \[ \begin{gathered} \ln y=x=\frac{\log y}{\log e}=\frac{\log y}{0.434294}=2.302585\,\log y. \end{gathered} \tag{2.29}\] Der natürliche Logarithmus beträgt also ungefähr das 2.3-fache des dekadischen Logarithmus.

Die Tatsache, dass \(\exp\) und \(\ln\) zueinander invers sind, bedeutet, dass die eine Funktion jeweils die Aktion der anderen rückgängig macht, also \[ \begin{gathered} (\ln\circ\exp)(x)=\ln(\exp(x))=\ln(e^x)=x,\quad x\in\mathbb R, \end{gathered} \tag{2.30}\] dabei bedeutet das Symbol \(\circ\) Verkettung oder Zusammensetzung (Kompositum). Weiters, \[ \begin{gathered} (\exp\circ\ln)(y)=\exp(\ln(y))=e^{\ln y}=y,\quad y>0. \end{gathered} \tag{2.31}\] Fragen nach \(\ln e^2\) oder \(e^{\ln 5}\) können daher ohne Heranziehen des Taschenrechners beantwortet werden. Insbesondere ist \(\ln e=\ln e^1=1\).

Die Rechengesetze für beliebige Potenzen gelten natürlich auch für Potenzen mit der Basis \(e\) und damit ist auch schon alles über das Rechnen mit \(\exp(x)=e^x\) gesagt. Die Funktion \(\ln\) ist bis auf einen multiplikativen Faktor mit \(\log\) sogar identisch, siehe (2.29), und daher können wir auch mit \(\ln\) rechnen, wie wir es vom Logarithmus \(\log\) gewöhnt sind.

Beispiel 2.57 (Rechengesetze für \(\exp\) und \(\ln\))

Das wichtigste Rechengesetz für die Exponentialfunktion ist das Gesetz \[ \begin{gathered} \exp(x+y)=\exp(x)\cdot\exp(y). \end{gathered} \tag{2.32}\] Es besagt: Summen werden in Produkte verwandelt. Dies ist klar, denn \[ \begin{gathered} \exp(x+y)=e^{x+y}=e^x\cdot e^y=\exp(x)\exp(y). \end{gathered} \] Ebenso wichtig die die Potenzierungsregel: \[ \begin{gathered} \left(\exp(x)\right)^y =(e^x)^y=\exp(x\cdot y). \end{gathered} \tag{2.33}\] Sie besagt: Potenzen werden in Produkte verwandelt.

Das wichtigste Rechengesetz für Logarithmen besagt, dass Produkte in Summen verwandelt werden, dh. \[ \begin{gathered} \ln (x\cdot y)=\frac{\log (x\cdot y)}{\log e}= \frac{\log x+\log y}{\log e}=\ln x+\ln y. \end{gathered} \tag{2.34}\] Beim Lösen von Exponentialgleichungen benötigen wir noch \[ \begin{gathered} \ln x^p=p\ln x, \end{gathered} \tag{2.35}\] was auf völlig analoge Weise auf das entsprechende Rechengesetz für \(\log\) zurückgeführt werden kann.

Wir können also eine Exponentialgleichung \(a^x=b\) sowohl mit dekadischen Logarithmen als auch mit natürlichen Logarithmen lösen: \[ \begin{gathered} x=\frac{\log y}{\log a}=\frac{\ln y}{\ln a}. \end{gathered} \] Das ist auch deshalb völlig klar, weil ja die Logarithmusfunktionen \(\log\) und \(\ln\) zueinander proportional sind.

Darstellung von Exponentialfunktionen

Wir wir zu Beginn erklärt haben, dient die Einführung der Exponentialfunktion \(\exp\) einfach der Vereinheitlichung. Es ist üblich, Exponentialfunktionen mit anderen Basen auf die Basis \(e\) umzurechnen und so durch \(\exp\) darzustellen. Wie geht das vor sich? Wie kann man die Exponentialfunktion \(f(x)=a^x\) auf die Basis \(e\) umrechnen?

Wir gehen dabei so vor, dass wir zunächst die Basis \(a\) als Potenz von \(e\) darstellen, also nach (2.31) \[ \begin{gathered} a=e^{\ln a}. \end{gathered} \tag{2.36}\] Daraus ergibt sich dann \[ \begin{gathered} f(x)=a^x=(e^{\ln a})^x=e^{x\ln a}. \end{gathered} \tag{2.37}\] Wir können also die Funktion \(f(x)=a^x\) in der Form \(f(x)=e^{cx}\) schreiben, wobei wir einen konstanten Faktor \(c\) einschieben müssen, der von der ursprünglichen Basis \(a\) abhängt, nämlich \(c=\ln a\).

Wir fassen zusammen:

Satz 2.58  

• Es gibt drei verschiedene Darstellungsarten einer Exponentialfunktion: \[ \begin{gathered} f(x)=Aa^x=A(1+r)^x=Ae^{cx}. \end{gathered} \]

• Dabei bezeichnet \(a\) den Wachstumsfaktor, \(r\) die relative (prozentuelle) Änderung und \(c\) den nominellen Zinssatz.

• Diese Größen hängen zusammen durch \[ \begin{gathered} a=1+r, \quad c=\ln a. \end{gathered} \]

Die Konstante \(c=\ln a\) hat eine inhaltliche Bedeutung, die uns schon vertraut ist. Das folgende Beispiel wird uns das zeigen.

Beispiel 2.59 (Kontinuierliche Verzinsung)

Ein Kapital von \(K(0)\) GE wird kontinuierlich so verzinst, dass es pro Jahr effektiv um 12 % wächst. Wir wollen das Kapitalwachstum als Exponentialfunktion durch \(\exp\) darstellen.

Der relative Zuwachs ist \(r=0.12\) pro Zeiteinheit (Jahr) und daher beträgt der Aufzinsungsfaktor (der Wachstumsfaktor) \(q=1+r=1.12\). Die Exponentialfunktion, die das Kapitalwachstum beschreibt, lautet daher \[ \begin{gathered} K(t)=K(0)\,1.12^t. \end{gathered} \] Wir wollen diese Darstellung nun durch eine Darstellung in der Form \(K(t)=K(0)e^{ct}\) ersetzen. Um \(c\) zu berechnen, bilden wir \(c=\ln q=\ln 1.12= 0.11333\) und erhalten so \[ \begin{gathered} K(t)=K(0)\,e^{t\ln q}=K(0)\,e^{0.11333\,t}=K(0)\exp(0.11333\,t). \end{gathered} \] Das ist die gesuchte Darstellung.

Es gibt noch einen anderen Weg. Wir berechnen den nominellen Zinssatz, der hinter der kontinuierlichen Verzinsung mit \(r=0.12\) steckt. Dies bedeutet, wir suchen eine Zahl \(c\) mit der Eigenschaft \[ \begin{gathered} q=1.12=\lim_{n\to\infty} \Big(1+\frac{c}{n}\Big)^n=e^c. \end{gathered} \tag{2.38}\] Die Gleichung \(q=e^c\) bedeutet aber das Gleiche wie \(c=\ln q=0.11333\) und wir sehen daraus, dass das die gleiche Zahl ist, die wir oben berechnet haben.

Nun ist uns klar, wie die Zahl \(c\) in der Darstellung (2.38) inhaltlich zu interpretieren ist: Sie ist nichts anderes als der nominelle Zinssatz. Die beiden Darstellungen des Kapitalwachstums durch Exponentialfunktionen mit verschiedenen Basen \[ \begin{gathered} K(t)=K(0)\,q^t=K(0)\,e^{ct} \end{gathered} \tag{2.39}\] haben somit unterschiedliche Interpretationen: Im ersten Fall erfolgt die Darstellung durch den Aufzinsungsfaktor \(q=1+r\), der auf dem effektiven Zinssatz \(r\) beruht. Im zweiten Fall erfolgt die Darstellung durch den nominellen Zinssatz \(c=\ln q\).

Musteraufgabe 2.60 Welcher nominelle Zinssatz ergibt bei kontinuierlicher Verzinsung einen effektiven Jahreszins von 10%?

Lösung: Wir bezeichnen wieder den nominellen Zinssatz mit \(c\) und den effektiven Zinssatz mit \(r\). Diese Größen hängen bei kontinuierlicher Verzinsung durch die Gleichung \(e^{c} = q = 1+r\) zusammen. Diese Exponentialgleichung müssen wir lösen: \[ \begin{aligned} e^{c}& = 1.1 \\ c\,\ln\,e& = \ln\,1.1\qquad\qquad (\ln\,e = 1) \\ c& = 0.09531\,. \end{aligned} \] Der nominelle Jahreszinssatz beträgt daher ca. 9.5 %. □

Musteraufgabe 2.61 Welcher nominelle Zinssatz verdreifacht bei kontinuierlicher Verzinsung ein Kapital im Lauf von \(15\) Jahren?

Lösung: Wir bezeichnen den nominellen Zinssatz mit \(c\) und den effektiven Zinssatz mit \(r\). Diese Größen hängen bei kontinuierlicher Verzinsung durch die Gleichung \(e^{c} = q = 1+r\) zusammen. Daher gilt \[ \begin{gathered} K(t)=\big(e^{c}\big)^{t}\cdot K(0)=e^{ct}\cdot K(0). \end{gathered} \] Der Angabetext führt auf die Gleichung \[ \begin{gathered} K(15) = e^{15c}\cdot K(0) = 3\,K(0). \end{gathered} \] Daraus ergibt sich eine Exponentialgleichung, die wir lösen können: \[ \begin{aligned} e^{15c}&=3 \\ 15c\,\ln\,e&= \ln\,3\qquad\qquad (\ln\,e = 1) \\ c& = \dfrac{\ln\,3}{15} = 0.073241\,. \end{aligned} \] Der nominelle Jahreszinssatz beträgt ca. 7.3 %. □

Musteraufgabe 2.62 Nach wievielen Jahren wird ein Anfangskapital verdreifacht, wenn es bei einem nominellen Zinssatz von \(5\%\) kontinuierlich verzinst wird?

Lösung: Wir bezeichnen den nominellen Zinssatz mit \(c\) und den effektiven Zinssatz mit \(r\). Diese Größen hängen bei kontinuierlicher Verzinsung durch die Gleichung \(e^{c} = q = 1+r\) zusammen. Daher gilt \[ \begin{gathered} K(t)=e^{ct}\cdot K(0). \end{gathered} \] Der Angabetext führt auf die Gleichung \[ \begin{gathered} K(t) = e^{0.05t}\cdot K(0) = 3\,K(0). \end{gathered} \] Daraus ergibt sich erneut eine Exponentialgleichung, die wir lösen können: \[ \begin{aligned} %% {alignat*}{2} e^{0.05t}& = 3 \\ 0.05t\,\ln\,e& = \ln\,3 \qquad\qquad (\ln\,e = 1) \\ t& = \dfrac{\ln\,3}{0.05} = 21.972246\simeq 22. \end{aligned} \] In \(22\) Jahren wird das Kapital verdreifacht. □

2.7 Weitere Übungsaufgaben

1. Ein Kapital \(K_0=2000\) GE wächst durch einfache Verzinsung im Lauf von 10 Jahren auf einen Endwert von 6000 GE. Wie hoch war der Zinssatz?

   Lösung: 20 %

2. Ein Kapital \(K_0\) wächst wird mit 3.5 % zusammengesetzt verzinst und wächst im Laufe von 12 Jahren auf einen Betrag von 18 208 GE. Berechnen Sie \(K_0\). Runden Sie das Ergebnis auf eine ganze Zahl.

   Lösung: \(K_0\simeq 12\,050\) GE

3. Jemand erhält für seine Eigentumswohnung zwei Kaufangebote, Angebot A: 200 000 sofort und bar auf die Hand. Angebot B: 220 000 GE, aber erst in zwei Jahren. Welches Angebot ist besser, wenn der Marktzins 5% beträgt?

   Lösung: Barwert \(A=200\,000\), Barwert \(B=199\,546\), A ist besser.

4. Ein Kapital von 19000 GE wird zu 11.53 % Zinsen für 14 Jahre angelegt. Nach 5 Jahren wird der Zinssatz gesenkt, sodass sich über die gesamt Laufzeit gerechnet nur mehr eine effektive Verzinsung von 9.916 % ergibt. Berechnen Sie auf welchen Wert der Zinssatz gesenkt wurde.

   Lösung: 9.02 %

5. Ein Vater legt bei einer Bank ein Kapital an, um seiner jetzt neunjährigen Tochter zum 24. Geburtstag ein Startkapital von 171 000 GE zu sichern. 5 Jahre nach der Einzahlung setzte die Bank den Zinssatz auf 3 % herab und der Vater musste zu diesem Zeitpunkt 36 143.91 GE nachzahlen, um die Endsumme zu sichern. Welchen Zinssatz hatte die Bank anfangs gewährt?

   Lösung: 6.5 %

6. Frau C gewährt ihrem Neffen ein Darlehen von 12 000 GE zur Finanzierung seines Studiums. Dieses Darlehen wird mit 5% Zinsen jährlich verzinst und ist mit Zins und Zinseszins zurückzuzahlen, sobald der Neffe promoviert. Tatsächlich zahlt der Neffe Frau C einen Betrag von 16 885 GE zurück. Wie lange hat er für sein Studium gebraucht? Runden Sie das Ergebnis auf die nächstgrößere ganze Zahl.

   Lösung: 7 Jahre

7. Nullkupon-Anleihen werden zu einem Nominale (Rückzahlungswert) von 1000 GE, garantierter Verzinsung mit 4.5 % und Laufzeit 10 Jahren angeboten. Zu welchem Preis?

   Lösung: 643.93 GE

8. Ein Zero Bond mit Nominale 10 000 GE und 5 Jahren Laufzeit wird zu einem Preis von 8 600 GE angeboten. Gegenwärtig beträgt der Marktzinssatz 3.75 %. Ist dieses Investment sinnvoll?

   Lösung: Nein, die Verzinsung des Bonds beträgt lediglich 3.06 %.

9. Jemand steigt als stiller Gesellschafter (Darlehensgeber) mit einem Betrag von 100000 GE bei einer Firma ein. Nach 5 Jahren erhält der Gesellschafter für seine Einlage 137000 GE zurück. Während der 5 Jahre wurden weder Zinsen noch Tilgung bezahlt. Berechnen Sie die jährliche Rendite des Investments.

   Lösung: 6.5 %

10. Eine Gemeinde legt ein Kapital zu 10.5 % Zinsen an, das in 20 Jahren auf 21 Mio. GE anwachsen und dann zum Bau eines Seniorenheimes verwendet werden soll. Nach 11 Jahren muss die Bank den Zinssatz herabsetzen. Um dennoch in der festgesetzten Zeit die erforderliche Endsumme zu erreichen, wird ein Betrag von 1 955 372 zugelegt. Wie stark ist der Zinssatz gesenkt worden?

    Lösung: 2.5 %

11. Frau X hat bei einer privaten Kreditagentur ein endfälliges Darlehen aufgenommen, das mit 17.3 % zu verzinsen ist. Ihr Anwalt rät ihr, wegen der hohen Zinsen Klage bei Gericht zu führen. Das Gericht gibt der Klage recht und setzt den Zinssatz auf 7.1 % herab. Dadurch reduzierte sich die Rückzahlungssumme von 93 712 auf 651̇27 GE. Was war die vereinbarte Laufzeit des Darlehens in Jahren?

    Lösung: 4 Jahre

12. Albrecht von Wallenstein, Herzog von Friedland, gewährte Kaiser Ferdinand II. 1628 ein Darlehen, für das er 28 % Zinsen verlangte. Unter dem Druck des Fürsten Harrach, der diesen Zins als unsittlich empfand, senkte Wallenstein freiwillig den Zinssatz auf 10 %. So kam es, dass Ferdinand II. nur 5710 statt 10469 Gulden zurückzuzahlen hatte. Wie hoch war das Darlehen und für wieviele Jahre war es gewährt worden?

    Lösung: \(t=4, K_0=3900\)

13. Eine Maschine, die 5 Jahre betriebsfähig ist, kostet 307 000 GE, die jährlichen Betriebskosten betragen 15 350 GE. Welchen jährlichen Ertrag (nachschüssig) muss die Maschine erbringen, wenn ihre Anschaffung kein Verlust sein soll und wenn 7 % Zinseszinsen berechnet werden? Runden Sie das Ergebnis auf eine ganze Zahl.

    Lösung: 90224 GE

14. Bei einer Versicherungsgesellschaft werden 930 000 GE gegen Entrichtung einer vorschüssigen jährlichen Prämie von 8 120 GE versichert. Nach wievielen Jahren ist bei 6.5 % Zinseszinsen das versicherte Kapital gedeckt? Runden Sie das Ergebnis auf eine ganze Zahl.

    Lösung: 33 Jahre

15. Ein mit 10 % verzinstes Kapital von 10̇70 000 GE soll zur Zahlung einer vorschüssigen Rente verwendet werden. Wie hoch dürfen die jährlichen Zahlungen maximal sein, damit die Rente mindestens 10 Jahre lang bezahlt werden kann? Runden Sie das Ergebnis auf eine ganze Zahl.

    Lösung: 158 307 GE

16. Die Anlage einer Autostraße kostet \(600\) Millionen GE, für die jährlichen Erhaltungskosten (vorschüssig) werden \(15\) Millionen veranschlagt. Diese Kosten sollen durch den Verkauf von Jahresvignetten hereingebracht werden. Wie hoch muss der Preis für eine Jahresvignette angesetzt werden, wenn durchschnittlich \(400\,000\) Autos jährlich erwartet werden, und das aufgewendete Kapital mit \(5\)% Verzinsung in \(25\) Jahren zurückgezahlt werden soll?

    Lösung: \(138.9\) GE

17. Jemand zahlt zu Beginn jedes Jahres einen Geldbetrag auf ein Sparbuch ein, um nach 7 Jahren eine Reise im Wert von 44 000 GE finanzieren zu können. Wie hoch muss dieser Geldbetrag mindestens sein, wenn die Verzinsung jährlich 5.5 % beträgt? Runden Sie das Ergebnis auf eine ganze Zahl.

    Lösung: 5045 GE

18. Zur Finanzierung einer vorschüssigen Rente der Höhe 11000 GE steht ein Kapital von 120 000 zur Verfügung. Wieviele Jahre kann die Rente ausbezahlt werden, wenn der Zinssatz 5 % beträgt?

    Lösung: 15 Jahre

19. Eine Standardanleihe (Plain Vanilla Bond) wird angeboten mit Nominale 10 000 GE, Laufzeit 15 Jahre und jährlichem Kupon von 530 GE, fällig am Jahresende, der langfristige Marktzins beträgt 4.2 %. Was ist der Ausgabepreis dieser Anleihe?

    Lösung: \(P=11\,206.10\) GE

20. Ein Kapital wird mit 7 % nominell verzinst. Nach wie vielen Jahren hat sich das Kapital bei unterjähriger Verzinsung mit 6 Verzinsungsperioden verdoppelt?

    Lösung: \(t=9.96\simeq 10\) Jahre

21. Man weiß, dass zwei Brüder, die vor 10 Jahren 600 000 GE geerbt haben, jetzt zusammen 862 100 GE besitzen. Wieviel hatte der eine, wieviel der andere geerbt, wenn der erste sein Geld mit 4% bei ganzjähriger Verzinsung, der zweite seinen Anteil mit 3.5 % bei halbjähriger Verzinsung angelegt hat?

    Lösung: 202 136.44 bzw. 397 863.56 GE

22. Ein Kapital von 38000 GE wird mit einem Zinssatz von 9.3 % kontinuierlich verzinst. Wie hoch ist das Kapital nach 5 Jahren?

    Lösung: 60 496.54 GE

23. In welcher Zeit hat sich ein Anfangskapital ver-2-facht, wenn es mit einem nominellen Zinssatz von 4.8 % kontinuierlich verzinst wird?

    Lösung: 14.44 Jahre

24. Ein Kapital \(K_0\) GE wird kontinuierlich so verzinst, dass es pro Jahr effektiv um 7 Prozent wächst. Berechnen Sie den nominellen Zinssatz.

    Lösung: 6.77 %

25. Welcher nominelle Zinssatz ver-2-facht bei kontinuierlicher Verzinsung ein Kapital im Laufe von 16 Jahren?

    Lösung: 4.33 %

26. Ein Kapital wird mit 11.5 Prozent nominell verzinst. Wie hoch ist der effektive Zinssatz bei kontinuierlicher Verzinsung?

    Lösung: 12.19 %

27. A gewährt dem B ein Darlehen über 100000 GE. B sichert zu, die Schuld in zwei Teilbeträgen zurückzuzahlen: 55000 GE am Ende des ersten Jahres, weitere 55000 GE am Ende des zweiten Jahres. Mit welchem Zinsatz war das Darlehen verzinst?

    Lösung: 6.6 %

---

1. Manchmal wird der Zinssatz als Prozentsatz angegeben. Das bedeutet lediglich, dass eine andere Zähleinheit zugrunde gelegt wird. Bei Prozentsätzen sind dies Hundertstel. Mit einem Zinssatz von 8 Prozent meint man den Zinssatz \(r=0.08\).
   Oft wird der Zinssatz mit dem Buchstaben \(i\) (interest) bezeichnet. Da der Buchstabe \(i\) aber in der Mathematik häufig für andere Zwecke eingesetzt wird, werden wir Zinssätze nicht mit \(i\) bezeichnen.

2. In Satz 2.22 ist der Funktionsterm des allgemeinen Glieds der Term einer Exponentialfunktion. Wir werden Exponentialfunktionen erst später genauer untersuchen.

3. Dies ist bei konstantem prozentuellen Wachstum nicht ganz korrekt.

4. Tatsächlich folgt die Existenz des Limes aus der erwähnten Monotonie und Beschränktheit der Folge \(q_n\).

5. Das ist sicher die historische Wurzel des Dezimalsystems.