1 Lineare und quadratische Funktionen
1.1 Lineare Funktionen
Unter den reellen Funktionen sind die linearen die einfachsten. Ihre Bedeutung ist aber nicht allein ihrer Einfachheit geschuldet. Lineare Funktionen werden oft auch dazu verwendet, komplizierte Funktionen zu approximieren.
1.1.1 Funktionsterme
Definition 1.1 Funktionen
Eine lineare Funktion hat als Definitionsbereich die Menge
Die Funktionsterme
1.1.2 Funktionsgraphen
Wie sieht der Funktionsgraph von linearen Funktionen aus? Was ist das Besondere an den Graphen von linearen Funktionen? Es wird sich herausstellen, dass die Funktionsgraphen von linearen Funktionen durch einen geradlinigen Verlauf gekennzeichnet sind.
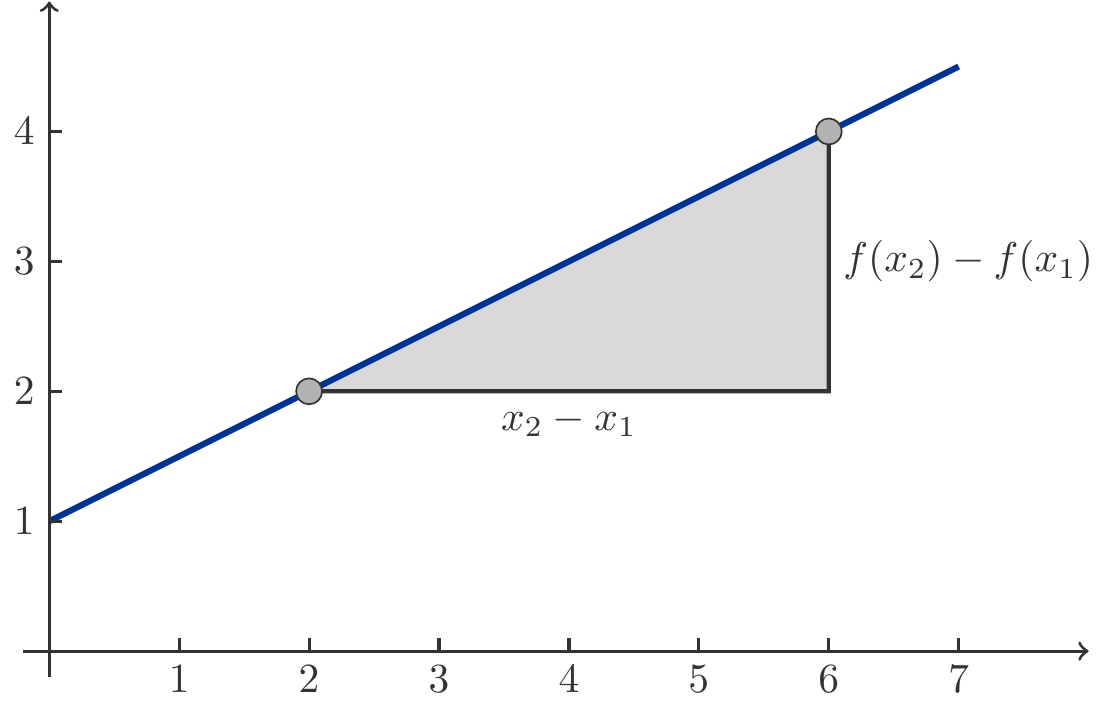
Was aber heißt geradlinig? Anschaulich ist das völlig klar, aber worin äußert sich die Geradlinigkeit mathematisch am Funktionsterm einer linearen Funktion? Um diese Fragen zu beantworten, erinnern wir uns an den Begriff des Steigungsverhältnisses.
Bemerkung 1.3 (Steigungsverhältnis) Betrachten wir zunächst eine völlig beliebige reelle Funktion
Eine erste Antwort besteht darin, die Differenz
Es sei nun
Diese Gleichung bedeutet, dass das Steigungsverhältnis des Graphen einer linearen Funktion unabhängig von der Wahl der Zahlen
Eine lineare Funktion
Bemerkung 1.4 (Geradengleichungen) Als Ergebnis unserer Überlegungen haben wir gesehen, dass der Funktionsgraph einer linearen Funktion stets eine Gerade ist. Allerdings ist die Umkehrung davon nicht richtig! Nicht jede Gerade ist der Funktionsgraph einer linearen Funktion. Es gibt ja auch Geraden, die senkrecht verlaufen. Solche Geraden haben kein Steigungsverhältnis und können daher nicht Funktionsgraphen von linearen Funktionen sein.
Beliebige Geraden werden in einem Koordinatensystem durch lineare Gleichungen der Form
Wenn
dass also
Bemerkung 1.5 (Berechnung der Parameter
Wir gehen so vor:
Aus der Gleichung
Musteraufgabe 1.6 Bestimmen Sie die Funktionsgleichung jener linearen Funktion, deren Graph durch die Punkte
1.1.3 Kosten und Erlöse
Wir besprechen nun einige wirtschaftliche Anwendungen von linearen Funktionen. Bei diesen Beispielen zeigt sich, dass der mathematisch maximal mögliche Definitionsbereich einer linearen Funktion meist nicht identisch ist mit dem Definitionsbereich, auf dem die Funktion eine wirtschaftlich sinnvolle Interpretation besitzt. Meist sind nur nichtnegative Werte
Lineare Kostenfunktionen
In vielen Bereichen entstehen Kosten, die eine lineare Funktion der verbrauchten Menge irgendwelcher Ressourcen sind.
Die Kosten, die ein Haushalt für den Verbrauch an elektrischem Strom zu entrichten hat, sind eine lineare Funktion der verbrauchten Strommenge (gemessen in Kilowattstunden). Diese lineare Kostenfunktion
Für jemanden, der über keinen Vertrag mit großzügiger Flat Rate verfügt, sind die Telefonkosten pro Monat eine lineare Funktion der verbrauchten Gesprächsminuten. Diese lineare Kostenfunktion
Auch bei der Produktion von Gütern sind lineare Kostenfunktionen ein einfaches, aber wichtiges mathematisches Modell. Es sei
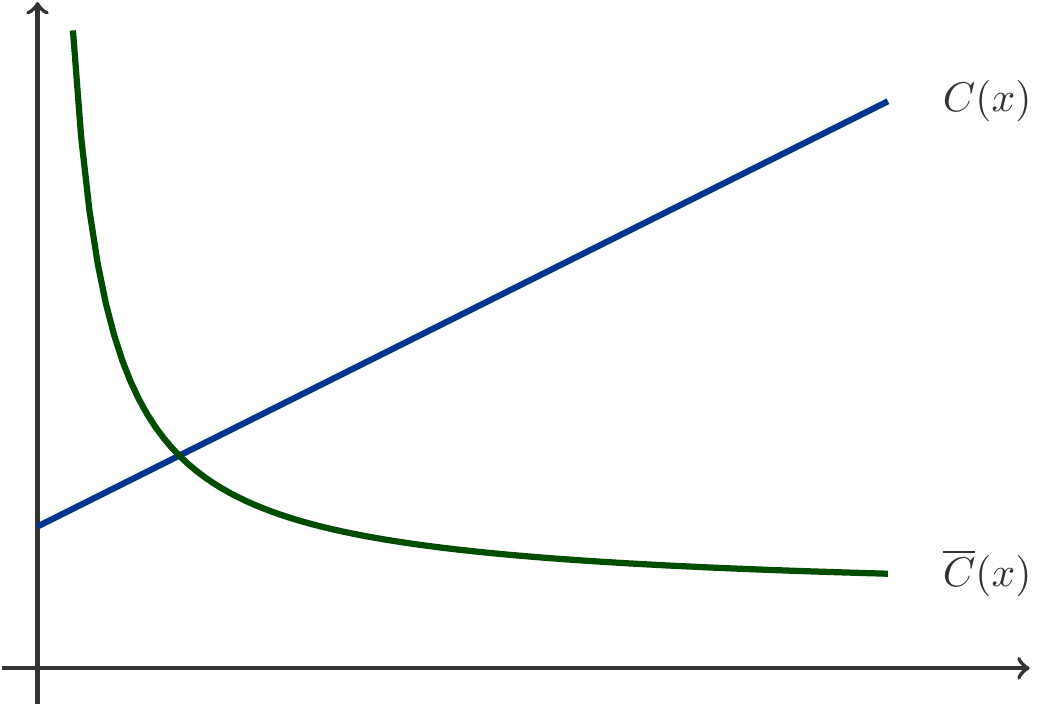
Wie hoch sind die Produktionskosten einer Mengeneinheit (Stückkosten), wenn eine lineare Kostenfunktion vorliegt?
Diese Frage besitzt zwei unterschiedliche Antworten je nachdem, was man unter den Produktionskosten einer Mengeneinheit versteht. Eine mögliche Interpretation versteht unter den Stückkosten die durchschnittlichen Kosten
Die durchschnittlichen Kosten enthalten also einen Anteil der Fixkosten
Eine andere mögliche Interpretation von Stückkosten meint jene Kosten, die durch die Produktion einer weiteren Mengeneinheit verursacht werden. Produzieren wir also beispielsweise die Menge
Sehen wir uns nun ein numerisches Beispiel an.
Musteraufgabe 1.7 Die Kostenfunktion laute
Lösung: Die durchschnittlichen Kosten betragen
Die Eigenschaft, dass die marginalen Kosten konstant sind, ist kennzeichnend für eine lineare Kostenfunktion. Sie zeigt auch die Anwendungsgrenzen des linearen Kostenmodells. Der Verlauf der marginalen Kosten ist in der Praxis meist nicht konstant.
Erlösfunktionen
Der Verkaufspreis einer Mengeneinheit eines Gutes betrage
Dass der Preis für die Marktteilnehmer eine gegebene Konstante ist, ist typisch für das Marktmodell der vollständigen Konkurrenz, auch Polypol genannt. In der Mikroökonomie versteht man darunter einen Markt, auf dem viele Anbieter vielen Nachfragern gegenüberstehen, so vielen jedenfalls, dass keiner der Marktteilnehmer über ausreichend Marktmacht verfügt, um durch autonome Aktionen den Marktpreis nachhaltig zu beeinflussen. Auf einem Monopolmarkt freilich sind die Verhältnisse völlig anders, wie wir in Abschnitt 1.2.2 sehen werden.
Rentabilität im linearen Kostenmodell
Es sei
Die Rentabilitätsbedingung lautet
Aber selbst dann, wenn
Im allgemeinen erhält man den Break-even-Point
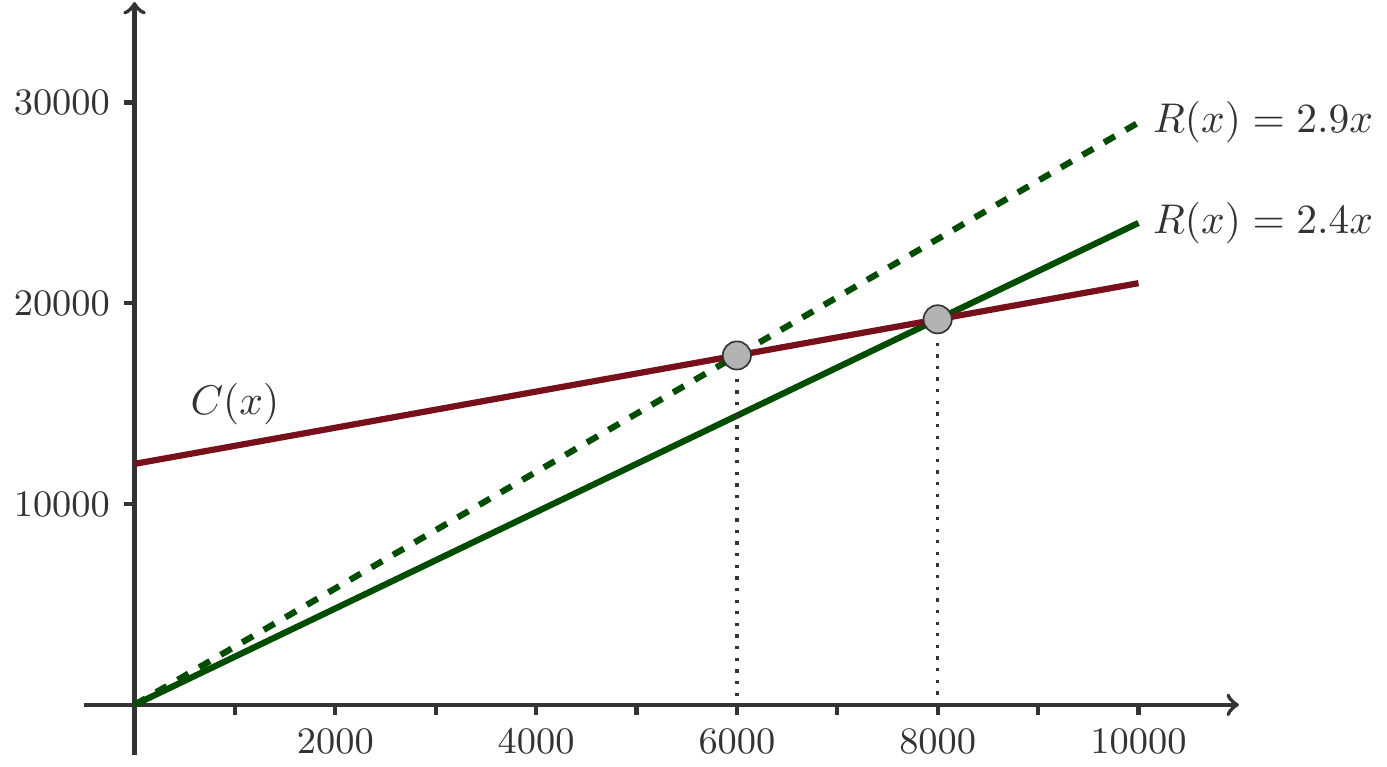
Musteraufgabe 1.8 Die Privatbrauerei Naturgold plant die Einführung eines neuen Produkts, eines Starkbiers, das unter dem Namen Favoritner Black Bock vertrieben werden soll. Lt. Planung werden die wöchentlichen Fixkosten der Produktion 12 000 GE betragen. Die variablen Kosten betragen pro Flasche Black Bock 0.9 GE, der Verkaufspreis wird mit 2.4 GE pro Flasche festgesetzt.
Wie lautet der Break-even-Point?
Wie müsste der Preis festgesetzt werden, damit der Break-even bei 6000 Flaschen erreicht wird?
Lösung: Aus dem Text der Angabe entnehmen wir die variablen Kosten pro Flasche
Musteraufgabe 1.9 Ein Unternehmen rechnet für die Produktion eines neuen Produktes mit Stückkosten von 45 GE. Die einmaligen Fixkosten für die Anschaffung der Produktionsmaschinen betragen 15000 GE. Pro Monat können 250 Stück des Produkts produziert werden. Wie soll der Preis pro Stück festgesetzt werden, wenn man nach vier Monaten einen Gewinn von 40000 GE erwirtschaftet haben will?
Lösung: Die Kostenfunktion lautet
Musteraufgabe 1.10 Ein Unternehmen plant die Einführung eines neuen Produktes, für das 60 000 GE als Fixkosten veranschlagt sind. Die Produktion eines Stücks verursacht Kosten von 150 GE. Bei 1200 Stück soll der Break-even-Point erreicht werden. Aufgrund eines Patentstreits muss die Produktion nach Erzeugung von 300 Stück abgebrochen werden. Welcher Schaden ist dem Unternehmen dadurch entstanden?
Lösung: Die Kostenfunktion lautet
Musteraufgabe 1.11 Ein Transportunternehmer kauft einen neuen LKW zu
Lösung: Zunächst formulieren wir die Kostenfunktion
1.2 Quadratische Funktionen
Neben den linearen Funktionen bilden die quadratischen Funktionen eine weitere einfache, aber sehr wichtige Klasse von reellen Funktionen.
1.2.1 Funktionsterme
Definition 1.12 Unter einer quadratischen Funktion versteht man eine reelle Funktion mit einem Funktionsterm der Form
Offenbar sind lineare Funktionen Spezialfälle von quadratischen Funktionen, wenn nämlich
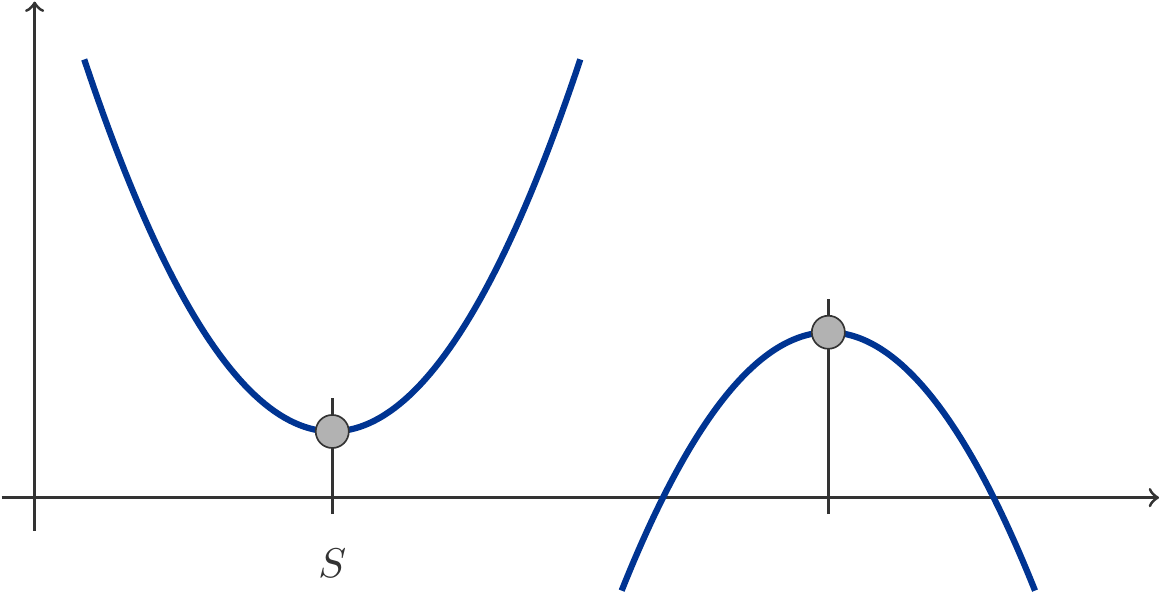
Ist
Musteraufgabe 1.13 Bestimme den Scheitel der quadratischen Funktion
Lösung: Es ist
1.2.2 Lineares Marktmodell (Monopol)
Wir werden in diesem Abschnitt typische Anwendungen kennenlernen, bei der die Analyse einer quadratischen Funktion im Vordergrund steht. Es geht um die Erlös- und Gewinnoptimierung eines Monopolisten. Dabei legen wir eine lineare Kostenfunktion und eine lineare Nachfragefunktion zugrunde. Das Problem der Gewinnoptimierung führt dann auf eine quadratische Funktion.
Erlösoptimierung
Ein Monopolist ist ein Anbieter, der sein Produkt als einziger auf dem Markt anbietet. Er kann den Preis seines Produkts beliebig wählen. Er steuert damit die Nachfrage nach seinem Produkt.
Angenommen, die Nachfragefunktion des Marktes lautet
Sehen wir uns ein Beispiel an.
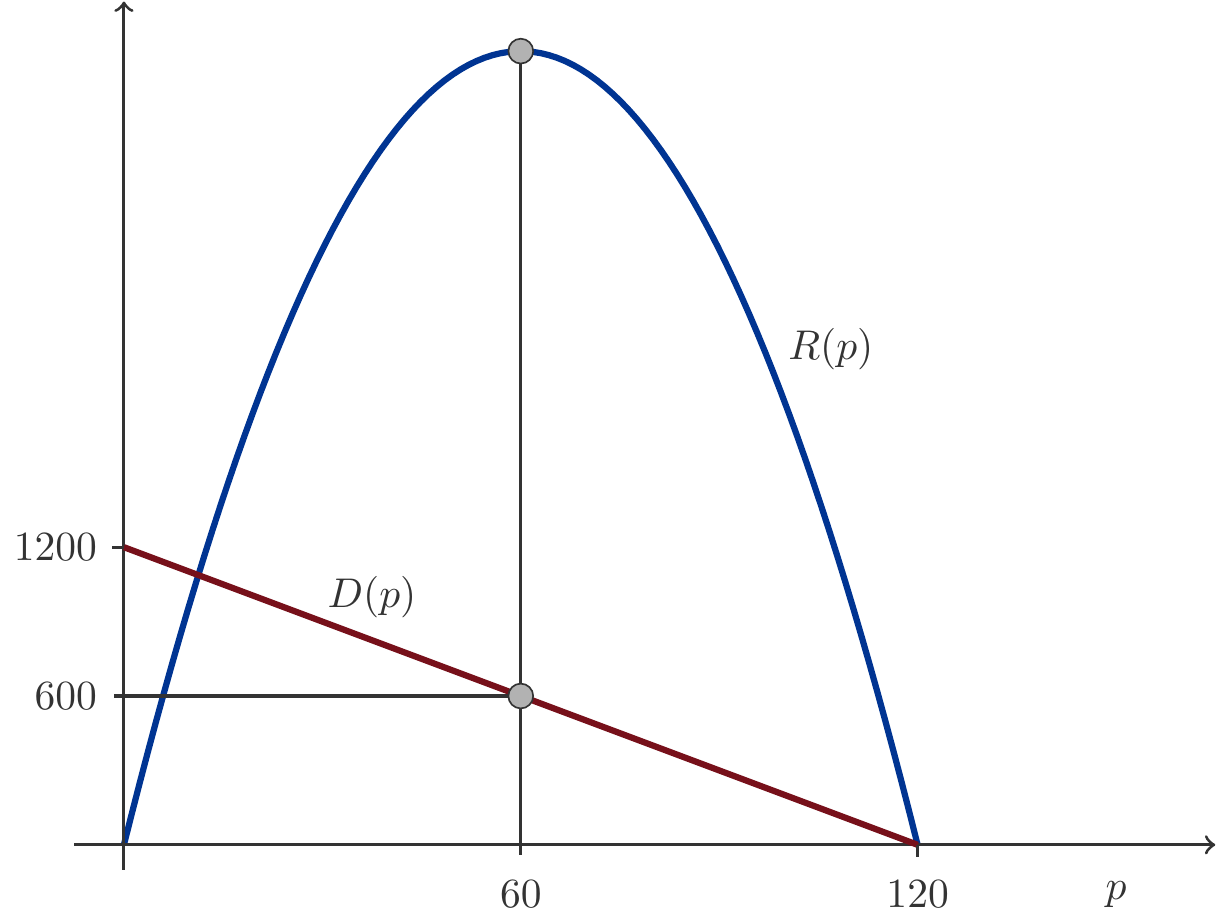
Musteraufgabe 1.14 Der Betreiber eines Skilifts besitzt in einem wunderschönen Skigebiet ein lokales Monopol. Vor zwei Jahren hatte der Betreiber bei einem Preis von 45 GE pro Stück 750 Tageskarten pro Tag verkaufen können. Als er im vergangenen Jahr den Preis auf 40 GE pro Karte senkte, stieg der Absatz auf 800 Karten pro Tag. Bei welchem Kartenpreis erzielt er die höchsten Einkünfte pro Tag?
Lösung: Zur Bestimmung der Erlösfunktion
Wir beantworten noch einige weitere Fragen.
Wie groß ist dann die Nachfrage?
Bei welchem Preis verschwindet die Nachfrage?
Abbildung 1.5 illustriert unsere Rechnung.
Musteraufgabe 1.15 Eine Tanzschule bietet Partnerkurse zum Preis von 5260 GE pro Person an. Eine Preiserhöhung um 460 GE führt zum Verlust eines Paares. Bei einem Preis von 10580 GE pro Person gibt es keinen Interessenten mehr. Bei welchem Preis erzielt die Tanzschule ihren höchsten Erlös?
Lösung: Es sei
Wie viele Personen werden bei dieser Preissetzung am Tanzkurs teilnehmen?
Gewinnoptimierung
In diesem Abschnitt lernen wir anhand konkreter Beispiele, wie für einfache Monopol- und Konkurrenzmärkte mit linearer oder quadratischer Kostenfunktion das Problem der Gewinnoptimierung mit elementaren Hilfsmitteln gelöst werden kann. Im Falle komplizierterer Kostenfunktionen sind wir allerdings auf Methoden der Differentialrechnung angewiesen, die wir erst in Kapitel 3 diskutieren werden.
Ein Beherbergungsbetrieb hat tägliche Fixkosten von 8000 GE. Die variablen Kosten pro Bett betragen 100 GE. Wenn
Es sei
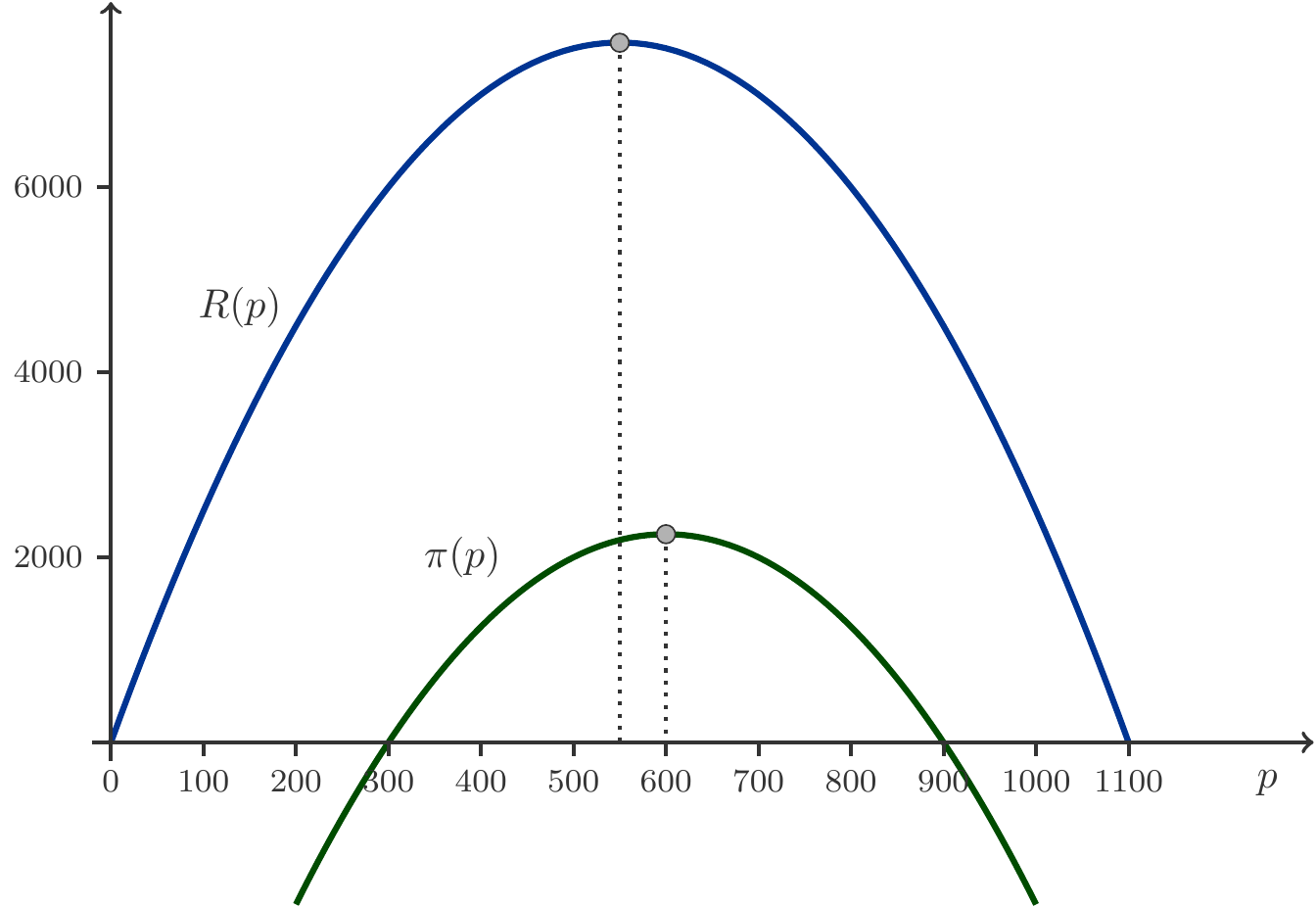
Musteraufgabe 1.17 Ein Fabrikant kann von einer Ware bei einem Preis von 120 GE 816 Stück, bei einem Preis von 240 GE aber nur 612 Stück absetzen. Dem Fabrikanten entstehen Fixkosten von 79600 GE und zusätzlich pro Stück Kosten von 60 GE. Berechnen Sie den Preis, bei dem der Fabrikant seinen größten Gewinn erzielt.
Lösung: Die Nachfragefunktion verläuft durch die Punkte
Musteraufgabe 1.18 Ein Unternehmen produziert ein Gut, das es zu einem Preis von 76 GE absetzen kann. Die Fixkosten der Produktion betragen 51700 GE, die variablen Kosten sind in Abhängigkeit von der produzierten Menge
Lösung: Der Gewinn als Funktion der abgesetzten Menge lautet:
Musteraufgabe 1.19 Ein Unternehmen produziert ein Gut, dessen Preis durch staatliche Verordnung auf 120 GE festgesetzt wurde. Die Fixkosten der Produktion betragen 60000 GE, die variablen Kosten sind in Abhängigkeit von der produzierten Menge
Eine (auch nur teilweise) Überwälzung der Steuer auf die Konsumenten ist nicht möglich.
Lösung: Es sei
Bemerkung 1.20 (Überwälzung der Steuer) In diesem Beispiel wurde ausdrücklich angenommen, dass aufgrund gesetzlicher Maßnahmen die Unternehmen die Steuer nicht einmal teilweise auf die Nachfrager überwälzen können. Wenn diese Maßnahmen nicht getroffen werden, bewirkt die Steuer eine Änderung der Lage der Angebotsfunktion der Unternehmen. Bei gleichem Preis wird weniger angeboten. Dies bewirkt, dass auch die Konsumenten einen Teil der Steuerlast tragen müssen. Dieses Problem wird ausführlich in der Theorie des partiellen Marktgleichgewichts der Mikroökonomie behandelt.
Musteraufgabe 1.21 Ein Unternehmen der chemischen Industrie besitzt aufgrund eines Patents ein Monopol auf Pflanzenschutzmittel. Die Nachfragefunktion nach diesem Produkt im Großhandel lautet
Lösung: Wir drücken zuerst in der Nachfragefunktion den Preis als Funktion der Angebotsmenge
1.3 Arithmetische Folgen
1.3.1 Folgen
Folgen sind Funktionen, die natürlichen Zahlen
Interessanter als konstante Folgen sind Zahlenfolgen, deren Werte sich zwar ändern, wobei aber die Veränderung selbst konstant ist. Die Folgenglieder solcher Folgen verändern sich vom Index
Definition 1.22 Eine Zahlenfolge
Hier einige Beispiele:
Die Folge mit dem allgemeinen Glied
Die Folge mit dem allgemeinen Glied
Die Folge mit dem allgemeinen Glied
Die Folge mit dem allgemeinen Glied
Folgenterme
Man kann am Term des allgemeinen Folgengliedes
Satz 1.23 Eine Folge mit dem allgemeinen Glied
Begründung: Es sei
Manchmal ist es naheliegender, die Folge mit
Es sei
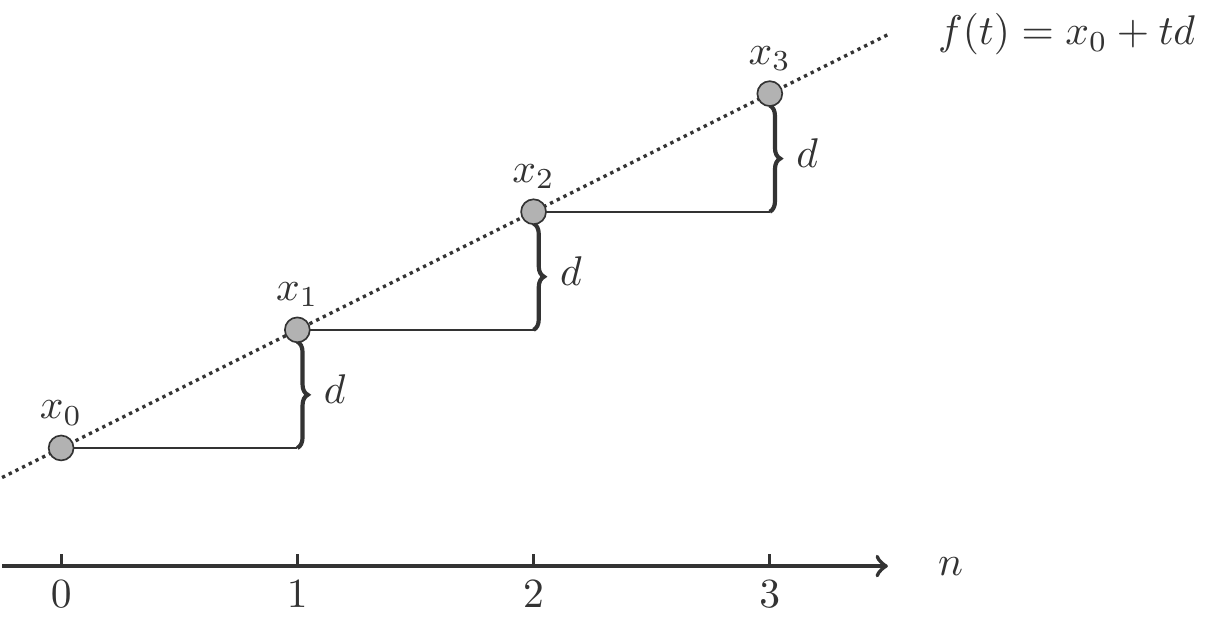
Graphische Darstellung
Es gibt also, wie wir gesehen haben, einen engen Zusammenhang zwischen arithmetischen Folgen und linearen Funktionen. Dieser Zusammenhang wird besonders deutlich, wenn man den Graphen einer arithmetischen Folge zeichnet. Ist
Der qualitative Verlauf des Graphen einer arithmetischen Folge hängt vom Vorzeichen der Differenz
Satz 1.24 Es sei
(1) Ist
(2) Ist
(3) Ist
Anwendungen
Wir sehen uns nun eine einfache Anwendung von arithmetischen Folgen an.
Ein Unternehmen will im dritten Jahr 7500 Stück eines Produktes herstellen und nach 10 Jahren das Produktionsniveau von 25 000 Stück erreichen. Die Produktionssteigerungen sollen jährlich konstant sein. Mit welcher Stückzahl muss im ersten Jahr begonnen werden und wieviel muss die jährliche Steigerung ausmachen?
Man kann diese Aufgabe sicherlich ohne jeden Bezug auf arithmetische Folgen ausschließlich mit dem Hausverstand lösen. Es ist aber nützlich, bereits bei einer so einfachen Aufgabe die mathematische Struktur des Problems deutlich zu machen.
Wir bezeichnen die Produktionszahlen der einzelnen Jahre mit
Da nun
1.3.2 Summierung von Folgen
Summenformel
Wir geben nun eine Formel an, mit der man die Summe einer arithmetischen Folge direkt berechnen kann.
Satz 1.26 Die Summe der ersten
Bemerkung 1.27 In der Abbildung 1.8 sind die ersten fünf Glieder der arithmetischen Folge
Die Summe der fünf Folgenglieder ist daher identisch mit der Summe der Flächeninhalte der fünf Balken. Dieser gesamte Flächeninhalt ist aber zugleich identisch mit dem Flächeninhalt unter jener Geraden, die die fünf Folgenglieder verbindet. Wenn wir diesen Flächeninhalt geometrisch berechnen, erhalten wir genau die Formel (1.8): Länge der Grundlinie
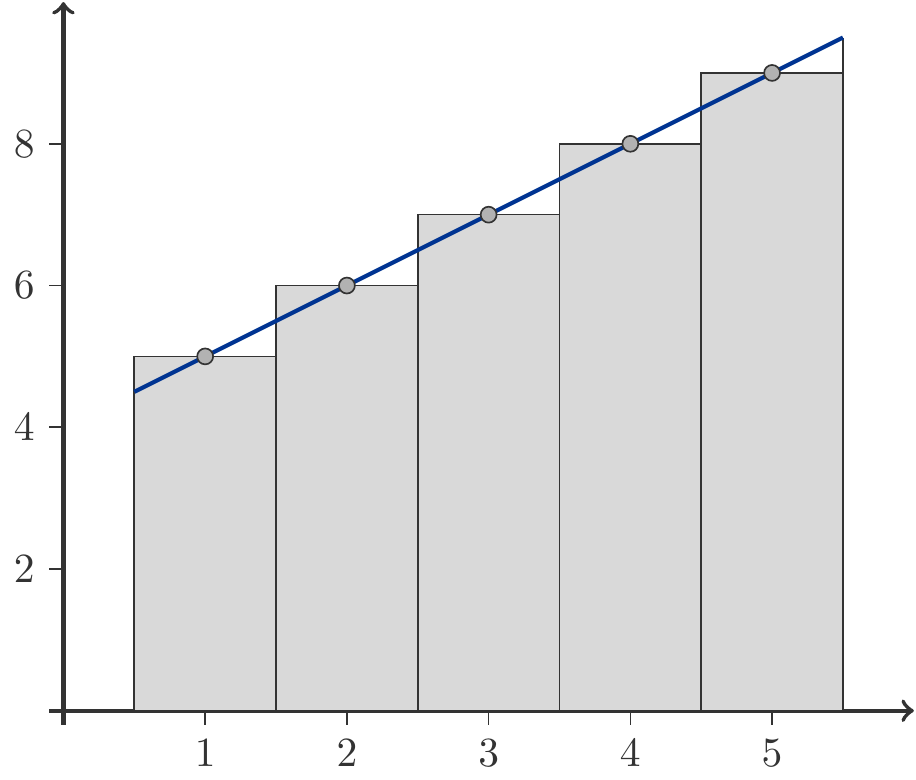
Nun zum Beweis der Summenformel (1.8). Der Beweistrick ist Teil der abendländischen Kulturgeschichte und gehört daher zur Allgemeinbildung.
Wir schreiben die Summe zweimal, in jeweils umgekehrter Reihenfolge, an und addieren übereinander stehende Folgenglieder:
Bemerkung 1.28 Es gibt noch andere Möglichkeiten, die Summe von
Anwendungen
Wo treten bei wirtschaftlichen Anwendungen Summen von arithmetischen Folgen auf? Wir beginnen zunächst mit einem einfachen Anwendungsbeispiel.
Musteraufgabe 1.29 Eine Bibliothek verleiht kostenlos Bücher an Studenten, die maximale Entlehnzeit beträgt 14 Tage. Wird diese Zeit überschritten, dann verrechnet die Bibliothek eine Strafgebühr von 6 GE pro Buch für den ersten Tag, und diese tägliche Strafgebühr erhöht sich von Tag zu Tag um weitere 2 GE. Wie hoch fällt die Strafe aus, wenn ein Buch um 8 Tage zu spät zurückgegeben wird?
Lösung: Die täglichen Strafgebühren bilden eine arithmetische Folge mit dem Anfangswert
Musteraufgabe 1.30 Die Baulandreserve einer Kleinstadt beträgt gegenwärtig 343000
Lösung: Die im ersten Jahr verbaute Fläche beträgt
Arithmetisch degressive Abschreibungen sind eine weitere Anwendung.
Musteraufgabe 1.31 Ein Wirtschaftsgut mit einem Anschaffungswert von 241 800 GE soll innerhalb von 12 Jahren arithmetisch degressiv abgeschrieben werden. Das heißt, die Abschreibungsbeträge bilden eine fallende arithmetische Folge
Lösung: Die vollständige Abschreibung innerhalb von 12 Jahren bedeutet, dass die Summe der Abschreibungsbeträge dem Anschaffungswert entsprechen soll. Bezeichnet man den letzten Abschreibungsbetrag mit
Die folgende Aufgabe stammt aus einem der bekanntesten Werke Leonhard Eulers, Vollständige Anleitung zur Algebra. Dieses Buch, das weite Verbreitung fand, ist 1770 erschienen. Auf Seite 163 findet sich:
Musteraufgabe 1.32 Jemand kauft ein Pferd unter der Bedingung, dass er für den ersten Hufnagel 5 Groschen, für den zweiten 8, für den dritten 11, und immer 3 Groschen mehr für jeden folgenden zahlen soll. Es sind aber im Ganzen 32 Nägel. Wieviel muss er für das Pferd bezahlen?
Lösung: Es sei
1.4 Weitere Übungsaufgaben
-
In einem Betrieb werden Rohre erzeugt. Die fixen Kosten für diese Produktion betragen 59400 GE, die variablen Kosten sind 157 GE pro Meter erzeugten Rohres. Beim Verkauf von einem Meter Rohr wird ein Erlös von 190 GE erzielt. Bei wieviel Metern Rohr wird der Break-even-Point erreicht?
Lösung:
-
Ein Hotel mit 930 Zimmern macht einen Gewinn von 210 GE pro Tag und belegtem Zimmer. Ein unbelegtes Zimmer verursacht einen Verlust von 100 GE pro Tag. Wieviele Zimmer müssen mindestens belegt sein, damit das Hotel ohne Verlust arbeiten kann?
Lösung:
-
Die fixen Kosten für die Anschaffung der Betriebsmittel zur Erzeugung einer Ware betragen 259578 GE. An einem Tag werden 69 Stück produziert, die Herstellungskosten pro Stück betragen 33 GE. Ein Stück wird um 90 GE verkauft. Nach wievielen Produktionstagen erreicht das Unternehmen den Break-even-Point?
Lösung:
-
Ein Unternehmen rechnet für die Produktion eines neuen Produkts mit Stückkosten von 52 GE. Die Fixkosten betragen 413480 GE. Pro Monat können 440 Stück hergestellt werden. Wie teuer soll die Ware verkauft werden, wenn man nach 11 Monaten einen Gewinn von 177000 GE erwirtschaftet haben will?
Lösung:
-
Eine Firma bringt ein neues Produkt auf den Markt, dessen Produktionskosten pro Stück 70 GE betragen, die kalkulierten monatlichen Fixkosten belaufen sich auf 78000 GE. Die Marketingabteilung des Unternehmens setzt den Preis des Produkts so fest, dass der Break-even-Point bei einer Ausbringung von 2000 Stück erreicht würde. Wegen eines zu spät erkannten Konstruktionsfehlers muss allerdings die Produktion schon nach 500 Stück eingestellt werden. Wie hoch ist der Verlust, der dem Unternehmen dadurch entstanden ist?
Lösung:
-
Eine Arbeitsagentur hat 600 Handwerker unter Vertrag. Kann ein Handwerker als Leiharbeiter vermittelt werden, dann beträgt der Tagesgewinn, der mit diesem Handwerker erzielt wird, 460 GE. Ein Handwerker, der nicht beschäftigt wird, verursacht hingegen einen Verlust von 140 GE pro Tag. Wieviele der Handwerker müssen pro Tag mindestens als Leiharbeiter vermittelt werden, sodass die Agentur keine Verluste macht?
Lösung:
-
Ein Monopolist setzt ein Gut ab, dessen Nachfrage in linearer Weise vom festgesetzten Preis abhängt. Der Monopolist erzielt maximalen Erlös bei einem Preis von 100 GE. Bei diesem Preis beträgt die Nachfrage 20 Stück. Wie groß wäre der Erlös bei einem Preis von 160 GE?
Lösung:
-
Ein Unternehmen produziert ein Gut, das es zu einem gesetzlich festgelegten Preis von 138 GE absetzen kann. Die Fixkosten der Produktion betragen 176000 GE, die variablen Kosten sind in Abhängigkeit von der produzierten Menge
Hinweis: Bei einem Umsatz von
Lösung:
-
Ein Unternehmen kann sein Produkt zu einem Preis von 100 GE absetzen. Es produziert mit der Kostenfunktion (
Lösung:
-
Ein Unternehmen produziert mit Kostenfunktion
Lösung:
-
Ein Unternehmen betreibt im Stadtzentrum eine Tiefgarage mit Stellplätzen für PKWs ausschließlich für Dauerparker, die Mindestlaufzeit eines Vertrags beträgt 1 Monat. In der Garage ist Platz für maximal 88 PKWs. Eine Auslastung von 75% wird erzielt, wenn das Monatsentgelt pro PKW 600 GE beträgt. Würde das Monatsentgelt um 100 GE erhöht, führte das zum Verlust eines Kunden. Wieviel soll für einen Stellplatz pro Monat verlangt werden, sodass der Erlös des Garagenbetreibers maximal wird?
Lösung:
-
Ein Unternehmen produziert ein Gut, das es zu einem Preis von 90 GE absetzen kann. Die Fixkosten der Produktion betragen 48200 GE, die variablen Kosten sind in Abhängigkeit von der produzierten Menge
Lösung:
-
Ein Monopolanbieter besitzt Nachfragefunktion
Lösung: gerundet
-
Ein Investitionsgut im Wert von
Lösung:
-
Jemand verpflichtet sich, 30 Jahre lang am Ende jeden Jahres einen Betrag zu zahlen, der Jahr für Jahr um einen konstanten Wert erhöht wird. Die Zahlung beträgt im 5. Jahr 3900 GE, im 20. Jahr 5400 GE. Wieviel ist insgesamt in den 30 Jahren zu bezahlen, ohne Berücksichtigung von Zinsen?
Lösung:
-
14500 Stück einer Ware sollen innerhalb von 29 Tagen verkauft werden. Am ersten Tag werden 150 Stück verkauft. Um wieviel Stück muss die verkaufte Stückzahl täglich gesteigert werden, damit nach 29 Tagen alle Waren verkauft sind?
Lösung:
-
Im ersten Jahr beträgt die Ausbeute einer Edelmetallmine 2500 Tonnen pro Jahr, allerdings sinkt diese pro Jahr gleichmäßig um 125 Tonnen. Bei der aktuellen Kostenstruktur des Bergbauunternehmens liegt der Break-even-Point bei 1625 Tonnen. Wieviele Jahre kann die Mine noch wirtschaftlich betrieben werden?
Lösung:
-
Die Finanzbehörden bewilligen der Firma X AG, die neu angeschaffte Schleudergussmaschine arithmetisch degressiv abzuschreiben. Berechnen Sie den 9. Abschreibungsbetrag, wenn die Anschaffungskosten der Maschine 376200 GE betragen und sie eine Nutzungsdauer von 11 Jahren hat.
Lösung:
-
In einem Paketverteilerzentrum sollen 9700 Pakete innerhalb von 25 Stunden den einzelnen Zustellern zugeteilt werden. In der ersten Stunde gelingt es, lediglich 40 Pakete zuzuteilen. Um wieviel Stück muss die Anzahl der zugeteilten Pakete pro Stunde gesteigert werden, sodass nach 25 Stunden alle Pakete zugeteilt sind?
Lösung:
Die Mineralölsteuer ist ein prominentes Beispiel für eine Mengensteuer.↩︎